Skip to content

Linear Transformation

Contents

Linear Transformation✔

선형변환(linear transformation, 선형사상, linear map, 벡터공간 준동형사상, vector space homomorphism)

F\mathbf{F}-벡터공간 V,W\mathbf{V} , \mathbf{W} 와 임의의 x,y∈Vx, y \in \mathbf{V} 와 임의의 c∈Fc \in \mathbf{F} 에 대하여 다음을 만족하는 함수 T⁡:V→W\operatorname{T}: \mathbf{V} \to \mathbf{W} 를 V\mathbf{V} 에서 W\mathbf{W} 로 가는 선형변환이라 한다.

  1. T⁡(x+y)=T⁡(x)+T⁡(y)\operatorname{T}(x + y) = \operatorname{T}(x) + \operatorname{T}(y)

  2. T⁡(cx)=cT⁡(x)\operatorname{T}(cx) = c\operatorname{T}(x)

  • 지금까지 벡터공간을 살펴보았는데 이제 벡터공간의 구조를 보존하는 함수를 다룬다. 이런 함수를 선형변환이라고 한다.

    미분연산자나 적분연산자가 선형변환의 대표적인 예시이다. 이런 연산자는 미분방정식과 적분방정식을 특정한 벡터공간에서 정의된 선형변환으로 이해할 수 있게 해준다. 기하학에서의 선형변환은 회전, 대칭, 사영 같은 것들이 있다.

    x,y∈V⟹x+y∈Vx, y \in \mathbf{V} \implies x+y \in \mathbf{V} 인데 T⁡(x),T⁡(y)∈W⟹T⁡(x+y)∈W\operatorname{T}(x), \operatorname{T}(y) \in \mathbf{W} \implies \operatorname{T}(x+y) \in \mathbf{W} 이므로 T⁡\operatorname{T} 가 벡터공간의 구조를 보존한다고 하는 것이다. 스칼라곱에 대해서도 마찬가지.

  • F=Q\mathbf{F} = \Bbb{Q} 이면 2) 는 1) 에서 도출된다. 그러나 일반적으로 1) 과 2) 는 독립된 명제이다.

  • T⁡\operatorname{T} 가 선형변환이라는 것을 편의상 "T⁡\operatorname{T} 는 선형(linear) 이다" 라고 한다.

  • 벡터공간의 준동형사상(vector space homomorphism) 이라는 정의는 준동형사상의 정의에 의하여 직관적을 알 수 있다.

선형변환의 성질

선형변환 T⁡:V→W\operatorname{T}: \mathbf{V} \to \mathbf{W} 는 다음 성질을 만족한다.

  1. T⁡\operatorname{T} 가 선형이면 T⁡(0)=0\operatorname{T}(0) = 0 이다.

  2. T⁡\operatorname{T} 가 선형이기 위한 필요충분조건은 ∀x,y∈V,∀c∈F:T⁡(cx+y)=cT⁡(x)+T⁡(y)\forall x, y \in \mathbf{V} , \forall c \in \mathbf{F} : \operatorname{T}(cx + y) = c\operatorname{T}(x) + \operatorname{T}(y) 이다.

  3. T⁡\operatorname{T} 가 선형이면 ∀x,y∈V:T⁡(x−y)=T⁡(x)−T⁡(y)\forall x, y \in \mathbf{V} : \operatorname{T}(x -y) = \operatorname{T}(x) - \operatorname{T}(y) 이다.

  4. T⁡\operatorname{T} 가 선형이기 위한 필요충분조건은 ∀x1,…,xn∈V,∀a1,…,an∈F\forall x_1, \dots, x_n \in \mathbf{V}, \forall a_1, \dots, a_n \in \mathbf{F} 에 대하여 다음이 성립하는 것이다.

    T⁡(∑i=1naixi)=∑i=1naiT⁡(xi) \operatorname{T} \bigg (\sum_{i=1}^{n}a_ix_i\bigg ) = \sum_{i=1}^{n}a_i\operatorname{T}(x_i)

  • 증명

    1:

    x=0x = 0 으로 두면 다음이 성립한다.

    T⁡(0+y)=T⁡(0)+T⁡(y)⟺T⁡(y)=T⁡(0)+T⁡(y)\operatorname{T} (0 + y) = \operatorname{T} (0) + \operatorname{T} (y) \iff \operatorname{T} (y) = \operatorname{T} (0) + \operatorname{T} (y)
    0=T⁡(0)0 = \operatorname{T} (0)

    2), 3), 4) 의 증명은 자명하다. ■

  • 1) 의 00 은 영벡터이다.

  • 어떤 함수가 선형임을 보일 때 주로 2) 를 사용한다.

  • 예시

    T⁡:R2→R2\operatorname{T}: \R ^{2} \to \R ^{2} 을 T⁡(a1,a2)=(2a1+a2,a1)\operatorname{T}(a_1, a_2) = (2a_1 + a_2, a_1) 이라 정의하고 이것이 선형인지 확인하자.

    c∈R,x=(b1,b2),y=(d1,d2)c \in \R, x = (b_1, b_2), y = (d_1, d_2) 라 하면 cx+y=(cb1+d1,cb2+d2)cx + y = (cb_1 + d_1, cb_2 + d_2) 이므로

    T⁡(cx+y)=(2(cb1+d1)+cb2+d2,cb1+d1) \operatorname{T}(cx + y) = (2(cb_1 + d_1) + cb_2 + d_2, cb_1 + d_1)

    이고 cT⁡(x)+T⁡(y)c\operatorname{T}(x) + \operatorname{T}(y) 도

    cT⁡(x)+T⁡(y)=(2(cb1+d1)+cb2+d2,cb1+d1) c\operatorname{T}(x) + \operatorname{T}(y) = (2(cb_1 + d_1) + cb_2 + d_2, cb_1 + d_1)

    이다. 그러므로 T⁡\operatorname{T} 는 선형이다.

  • 선형대수학은 기하학에서 널리 사용되는데, 이는 중요한 기하 변환들이 선형이기 때문이다.

  • 예시

    각 θ\theta 에 대하여 T⁡θ:R2→R2\operatorname{T} _{\theta }: \R ^{2} \to \R ^{2} 을

    T⁡θ(a1,a2)={(a1,a2) 를 반시계 방향으로 θ 만큼 회전한 벡터(a1,a2)≠(0,0)(0,0)(a1,a2)=(0,0) \operatorname{T} _{\theta } (a_1, a_2) = \begin{cases} (a_1, a_2) \text{ 를 반시계 방향으로 } \theta \text{ 만큼 회전한 벡터} & (a_1, a_2) \neq (0, 0)\\ (0, 0) & (a_1, a_2) = (0, 0) \\ \end{cases}

    와 같이 정의하면 T⁡θ:R2→R2\operatorname{T} _{\theta}: \R ^{2} \to \R ^{2} 는 2차원 좌표평면의 벡터를 θ\theta 만큼 회전하는 선형변환이다. 참고로 T⁡θ\operatorname{T} _{\theta} 는 형식적으로

    T⁡θ(a1,a2)=(a1cos⁡θ−a2sin⁡θ,a1sin⁡θ+a2cos⁡θ) \operatorname{T} _{\theta}(a_1, a_2) = (a_1 \cos \theta - a_2 \sin \theta, a_1 \sin \theta + a_2 \cos \theta)

    로 정의할 수 있다.

  • 예시

    T⁡:R2→R2,(a1,a2)↦(a1,−a2)\operatorname{T}: \R ^{2} \to \R ^{2} , (a_1, a_2) \mapsto (a_1, -a_2) 는 xx축 대칭(reflection about x-axis)이라는 선형변환이다.

  • 예시

    T⁡:R2→R2,(a1,a2)↦(a1,0)\operatorname{T}: \R ^{2} \to \R ^{2} , (a_1, a_2) \mapsto (a_1, 0) 는 xx축으로 사영(projection on the x-axis)이라는 선형변환이다.

  • 예시

    T⁡:Fm×n→Fn×m,A↦A⊤\operatorname{T}: \mathbf{F}^{m \times n} \to \mathbf{F}^{n \times m}, A \mapsto A ^{\top} 는 선형변환이다.

  • 예시

    무한번 미분가능한 함수 f:R→Rf: \R \to \R 의 집합 V\mathbf{V} 을 정의하면 V\mathbf{V} 는 R\R-벡터공간이된다. 이때 T⁡:V→V,f↦f′\operatorname{T}: \mathbf{V} \to \mathbf{V} , f \mapsto f' 로 정의하면

    T⁡(ag+h)=(ag+h)′=ag′+h′=aT⁡(g)+T⁡(h) \operatorname{T}(ag+h) = (ag+h)' = ag'+h'=a\operatorname{T}(g) +\operatorname{T}(h)

    이므로 선형변환이다.

  • 예시

    V\mathbf{V} 를 R\R 에서 정의한 모든 연속함수 집합으로 정의하고, a,b∈R,a<ba, b \in \R, a < b 에 대하여 T⁡:V→R,f↦∫abf(t)dt\operatorname{T}: \mathbf{V} \to \R, f \mapsto \int_{a}^{b}f(t)dt 로 정의하면 이는 선형변환이다. 왜냐하면

    ∫ab{pf(t)+qg(t)}dt=p∫abf(t)dt+q∫abg(t)dt \int_{a}^{b}\{pf(t) + qg(t)\}dt = p \int_{a}^{b}f(t)dt + q \int_{a}^{b}g(t)dt

    이기 때문이다.

Identity Transformation✔

항등변환(identity transformation)

F\mathbf{F}-벡터공간 V\mathbf{V} 에 대하여 I⁡V:V→V,x↦x\operatorname{I} _{\mathbf{V} }: \mathbf{V} \to \mathbf{V}, x \mapsto x 로 정의된 선형변환이다.
  • 항등변환 I⁡V\operatorname{I} _{\mathbf{V} } 을 편의상 I⁡\operatorname{I} 라 표기하기도 한다.

Zero Transformation✔

영변환(zero transformation)

F\mathbf{F}-벡터공간 V,W\mathbf{V} , \mathbf{W} 에 대하여 T⁡0:V→W,x↦0\operatorname{T} _{ 0}: \mathbf{V} \to \mathbf{W}, x \mapsto 0 로 정의된 선형변환이다.

Null Space, Range✔

영공간(null space, kernel)

벡터공간 V,W\mathbf{V}, \mathbf{W} 와 선형변환 T⁡:V→W\operatorname{T}: \mathbf{V} \to \mathbf{W} 에 대하여 영공간은 다음과 같은 집합이다.

ker⁡(T⁡)={x∈V:T⁡(x)=0} \ker(\operatorname{T}) = \{x \in \mathbf{V} : \operatorname{T}(x) = 0\}

  • 선형변환 T⁡:V→W\operatorname{T}: \mathbf{V} \to \mathbf{W} 의 영공간을 N⁡(T⁡)\operatorname{N}(\operatorname{T}) 또는 Null(T⁡)\text{Null}(\operatorname{T}) 또는 ker⁡(T⁡)\ker(\operatorname{T}) 로 표기한다.

  • 예시

    항등변환 I⁡:V→V\operatorname{I} : \mathbf{V} \to \mathbf{V} 에 대하여 ker⁡(I⁡)={0}\ker(\operatorname{I}) = \{0\} 이다.

    영변환 T⁡0:V→W\operatorname{T}_0 : \mathbf{V} \to \mathbf{W} 에 대하여 ker⁡(T⁡0)=V\ker(\operatorname{T}_0) = \mathbf{V} 이다.

상공간(range, image)

벡터공간 V,W\mathbf{V}, \mathbf{W} 와 선형변환 T⁡:V→W\operatorname{T}: \mathbf{V} \to \mathbf{W} 에 대하여 상공간은 다음과 같은 집합이다.

im⁡(T⁡)={T⁡(x)∈W:x∈V} \operatorname{im}(\operatorname{T}) = \{\operatorname{T}(x) \in \mathbf{W} : x \in \mathbf{V} \}

  • 선형변환 T⁡:V→W\operatorname{T}: \mathbf{V} \to \mathbf{W} 의 상공간을 R⁡(T⁡)\operatorname{R}(\operatorname{T}) 또는 ran⁡(T⁡)\operatorname{ran}(\operatorname{T}) 또는 im⁡(T⁡)\operatorname{im}(\operatorname{T}) 으로 표기한다.

  • 예시

    항등변환 I⁡:V→V\operatorname{I} : \mathbf{V} \to \mathbf{V} 에 대하여 im⁡(I⁡)=V\operatorname{im}(\operatorname{I}) = \mathbf{V} 이다.

    영변환 T⁡0:V→W\operatorname{T}_0 : \mathbf{V} \to \mathbf{W} 에 대하여 im⁡(T⁡0)={0}\operatorname{im}(\operatorname{T}_0) = \{0\} 이다.

정리 2.1

벡터공간 V,W\mathbf{V} ,\mathbf{W} 와 선형변환 T⁡:V→W\operatorname{T}:\mathbf{V} \to \mathbf{W} 에 대하여 ker⁡(T⁡),im⁡(T⁡)\ker(\operatorname{T}), \operatorname{im}(\operatorname{T}) 는 각각 V,W\mathbf{V} , \mathbf{W} 의 부분공간이다.

  • 다음 그림과 같다.

  • 증명

    V,W\mathbf{V} , \mathbf{W} 의 영벡터를 각각 0V,0W0 _{\mathbf{V} },0 _{\mathbf{W} } 라 하자.

    T⁡(0V)=0W\operatorname{T}(0 _{\mathbf{V} }) = 0 _{\mathbf{W} } 이므로 0V∈ker⁡(T⁡)0 _{\mathbf{V} } \in \ker(\operatorname{T}) 이다. x,y∈ker⁡(T⁡)x, y \in \ker(\operatorname{T}), c∈Fc \in \mathbf{F} 에 대하여

    T⁡(x+y)=T⁡(x)+T⁡(y)=0W+0W=0W,T⁡(cx)=cT⁡(x)=c0W=0W \begin{align}\begin{split} \operatorname{T}(x+y)&= \operatorname{T}(x)+\operatorname{T}(y)\\ &= 0 _{\mathbf{W} }+0 _{\mathbf{W} }\\ &=0 _{\mathbf{W} }, \enspace \operatorname{T}(cx) \\ &= c\operatorname{T}(x) = c 0 _{\mathbf{W} } = 0 _{\mathbf{W} } \\ \end{split}\end{align} \tag*{}

    이므로 x+y∈ker⁡(T⁡),cx∈ker⁡(T⁡)x+y \in \ker(\operatorname{T}), cx \in \ker(\operatorname{T}) 이다. 따라서 ker⁡(T⁡)\ker(\operatorname{T}) 은 V\mathbf{V} 의 부분공간이다. ▲

    T⁡(0V)=0W\operatorname{T}(0 _{\mathbf{V} }) = 0 _{\mathbf{W} } 이므로 0W∈im⁡(T⁡)0 _{\mathbf{W} } \in \operatorname{im}(\operatorname{T}) 이다. x,y∈im⁡(T⁡),c∈Fx, y \in \operatorname{im}(\operatorname{T}), c \in \mathbf{F} 에 대하여 다음을 만족하는 v,w∈Vv, w \in \mathbf{V} 가 존재한다.

    T⁡(v)=x,T⁡(w)=y \operatorname{T}(v) = x, \operatorname{T}(w) = y

    따라서

    T⁡(v+w)=T⁡(v)+T⁡(w)=x+y,T⁡(cv)=cT⁡(v)=cx \operatorname{T}(v+w) =\operatorname{T}(v) +\operatorname{T}(w) = x+y, \enspace \operatorname{T}(cv) = c\operatorname{T}(v) = cx

    이고, x+y∈im⁡(T⁡),cx∈im⁡(T⁡)x+y \in \operatorname{im}(\operatorname{T}), cx \in \operatorname{im}(\operatorname{T}) 이다. 그러므로 im⁡(T⁡)\operatorname{im}(\operatorname{T}) 는 W\mathbf{W} 의 부분공간이다. ■

정리 2.2

벡터공간 V,W\mathbf{V} ,\mathbf{W} 와 선형변환 T⁡:V→W\operatorname{T}: \mathbf{V} \to \mathbf{W} 와 V\mathbf{V} 의 기저 β={v1,v2,…,vn}\beta = \{v_1, v_2, \dots, v_n\} 에 대하여 다음이 성립한다.

im⁡(T⁡)=span⁡(T⁡(β))=span⁡({T⁡(v1),T⁡(v2),…,T⁡(vn)}) \operatorname{im}(\operatorname{T}) = \operatorname{span}(\operatorname{T}(\beta )) = \operatorname{span}(\{\operatorname{T}(v_1), \operatorname{T}(v_2), \dots, \operatorname{T}(v_n)\})

  • 이 정리는 선형변환의 상공간을 생성하는 방법을 알려준다.

  • 이 정리는 β\beta 가 무한집합일 때도 성립한다. 즉, 다음이 성립한다.

    im⁡(T⁡)=span⁡({T⁡(v):v∈β}) \operatorname{im}(\operatorname{T}) = \operatorname{span}(\{\operatorname{T}(v) : v \in \beta \})

  • 증명

    T⁡(β)⊂im⁡(T⁡)\operatorname{T}(\beta) \subset \operatorname{im}(\operatorname{T}) 이고 im⁡(T⁡)\operatorname{im}(\operatorname{T}) 가 부분공간이므로 정리 1.5 에 의하여

    span⁡({T⁡(v1),T⁡(v2),…,T⁡(vn)})=span⁡(T⁡(β))⊂im⁡(T⁡) \operatorname{span}(\{\operatorname{T}(v_1), \operatorname{T}(v_2), \dots, \operatorname{T}(v_n)\}) =\operatorname{span}(\operatorname{T}(\beta )) \subset \operatorname{im}(\operatorname{T})

    이다. ▲

    w∈im⁡(T⁡)w \in \operatorname{im}(\operatorname{T}) 이면 w=T⁡(v)w = \operatorname{T}(v) 을 만족하는 v∈Vv \in \mathbf{V} 가 존재하는데 β\beta 가 V\mathbf{V} 의 기저이므로 a1,a2,…,an∈Fa_1, a_2, \dots, a_n \in \mathbf{F} 에 대하여

    v=∑i=1naivi v = \sum_{i=1}^{n}a_iv_i

    이다. T⁡\operatorname{T} 는 선형이므로

    w=T⁡(v)=T⁡(∑i=1naivi)=∑i=1naiT⁡(vi)∈span⁡(T⁡(β))w = \operatorname{T}(v) = \operatorname{T} \bigg (\sum_{i=1}^{n}a_iv_i\bigg ) = \sum_{i=1}^{n}a_i\operatorname{T}(v_i) \in \operatorname{span}(\operatorname{T}(\beta ))

    이다. 이는 ∀w∈im⁡(T⁡)⟹w∈span⁡(T⁡(β))\forall w \in \operatorname{im}(\operatorname{T}) \implies w \in \operatorname{span}(\operatorname{T}(\beta )) 을 뜻하므로

    im⁡(T⁡)⊂span⁡(T⁡(β))=span⁡({T⁡(v1),T⁡(v2),…,T⁡(vn)}) \operatorname{im}(\operatorname{T}) \subset \operatorname{span}(\operatorname{T}(\beta )) = \operatorname{span}(\{\operatorname{T}(v_1), \operatorname{T}(v_2), \dots, \operatorname{T}(v_n)\})

    이 된다. ■

  • 다음 예시는 이 정리를 사용하여 im⁡(T⁡)\operatorname{im}(\operatorname{T}) 의 기저와 ker⁡(T⁡)\ker(\operatorname{T}) 의 기저를 쉽게 찾을 수 있다는 것을 말해준다.

  • 예시

    선형변환 T⁡:P2(R)→R2×2\operatorname{T}: \mathbf{P} _2(\R) \to \R ^{2 \times 2} 을

    선형변환 T⁡:P2(R)→R2×2\operatorname{T}: \mathbf{P} _2(\R) \to \R ^{2 \times 2} 을

    T⁡(f(x))=(f(1)−f(2)00f(0)) \operatorname{T}(f(x)) = \begin{pmatrix} f(1)-f(2) & 0\\ 0 & f(0)\\ \end{pmatrix}

    와 같이 정의하자. P2(R)\mathbf{P} _2(\R) 의 기저는 β={1,x,x2}\beta = \{1,x,x ^{2}\} 이므로 이 정리를 사용하여 im⁡(T⁡)\operatorname{im}(\operatorname{T}) 를 다음과 같이 나타낼 수 있다.

    im⁡(T⁡)=span⁡(T⁡(β))=span⁡({T⁡(1),T⁡(x),T⁡(x2)})=span⁡({(0001),(−1000),(−3000)})=span⁡({(0001),(−1000)}) \begin{align}\begin{split} \operatorname{im}(\operatorname{T}) &= \operatorname{span}(\operatorname{T}(\beta )) = \operatorname{span}(\{\operatorname{T}(1), \operatorname{T}(x), \operatorname{T}(x ^{2})\}) \\ &= \operatorname{span}\bigg (\bigg \{ \begin{pmatrix} 0 & 0\\ 0 & 1\\ \end{pmatrix}, \begin{pmatrix} -1 & 0\\ 0 & 0\\ \end{pmatrix}, \begin{pmatrix} -3 & 0\\ 0 & 0\\ \end{pmatrix} \bigg \}\bigg ) \\ &= \operatorname{span}\bigg (\bigg \{ \begin{pmatrix} 0 & 0\\ 0 & 1\\ \end{pmatrix}, \begin{pmatrix} -1 & 0\\ 0 & 0\\ \end{pmatrix} \bigg \}\bigg ) \end{split}\end{align}\tag*{}

    이로써 im⁡(T⁡)\operatorname{im}(\operatorname{T}) 의 기저를 찾았고 dim⁡(im⁡(T⁡))=2\dim(\operatorname{im}(\operatorname{T})) = 2 임을 알 수 있다. ▲

    이제 ker⁡(T⁡)\ker(\operatorname{T}) 의 기저를 찾아보자. 2×22 \times 2 영행렬 OO 에 대하여 f(x)∈ker⁡(T⁡)⟺T⁡(f(x))=Of(x) \in \ker(\operatorname{T}) \iff \operatorname{T}(f(x)) = O 이므로

    f(x)∈ker⁡(T⁡)⟺(f(1)−f(2)00f(0))=(0000) f(x) \in \ker(\operatorname{T}) \iff \begin{pmatrix} f(1) - f(2) & 0\\ 0 & f(0)\\ \end{pmatrix} = \begin{pmatrix} 0&0\\ 0&0\\ \end{pmatrix}

    이다. f(x)=a+bx+cx2f(x) = a + bx + cx ^{2} 라 하면

    0=f(1)−f(2)=−b−3c0=f(0)=a \begin{align}\begin{split} 0&= f(1) - f(2) = -b -3c\\ 0 &= f(0) = a \end{split}\end{align}\tag*{}

    이므로

    f(x)=c(−3x+x2) f(x) = c(-3x + x ^{2})

    이다. 따라서 ker⁡(T⁡)\ker(\operatorname{T}) 의 기저는 {−3x+x2}\{-3x + x ^{2}\} 이다. ▲

  • 위 예시에서 dim⁡(ker⁡(T⁡))+dim⁡(im⁡(T⁡))=1+2=3=dim⁡(P2(R))\dim(\ker(\operatorname{T})) + \dim(\operatorname{im}(\operatorname{T})) = 1 + 2 = 3 = \dim(\mathbf{P} _2(\R)) 이 성립하였는데 이는 정리 2.3 에서와 같이 일반적으로 성립한다.

Nullity✔

영공간의 차원(Nullity)

벡터공간 V,W\mathbf{V} , \mathbf{W} 와 선형변환 T⁡:V→W\operatorname{T}: \mathbf{V} \to \mathbf{W} 에 대하여 ker⁡(T⁡)\ker(\operatorname{T}) 가 유한차원 일 때 ker⁡(T⁡)\ker(\operatorname{T}) 의 차원을 다음과 같이 정의한다.

nullity⁡(T⁡)=dim⁡(ker⁡(T⁡)) \operatorname{nullity}(\operatorname{T}) = \dim(\ker(\operatorname{T}))
  • 지금까지 우리는 부분공간의 크기를 가늠할 때 차원을 사용했다. 영공간의 차원은 특히 중요하므로 새로운 이름 nullity⁡\operatorname{nullity} 을 붙혀서 다룬다.

Rank✔

랭크(rank), 계수

벡터공간 V,W\mathbf{V} , \mathbf{W} 와 선형변환 T⁡:V→W\operatorname{T}: \mathbf{V} \to \mathbf{W} 에 대하여 im⁡(T⁡)\operatorname{im}(\operatorname{T}) 가 유한차원 일 때 im⁡(T⁡)\operatorname{im}(\operatorname{T}) 의 차원을 다음과 같이 정의한다.

rank⁡(T⁡)=dim⁡(im⁡(T⁡)) \operatorname{rank}(\operatorname{T}) = \dim(\operatorname{im}(\operatorname{T}))
  • 지금까지 우리는 부분공간의 크기를 가늠할 때 차원을 사용했다. 상공간의 차원은 특히 중요하므로 새로운 이름 rank⁡\operatorname{rank} 을 붙혀서 다룬다.

Dimension Theorem✔

정리 2.3 차원정리(dimension theorem, rank-nullity theorem, fundamental theorem of linear mapping)

벡터공간 V,W\mathbf{V} , \mathbf{W} 와 선형변환 T⁡:V→W\operatorname{T}: \mathbf{V} \to \mathbf{W} 에 대하여 V\mathbf{V} 가 유한차원이면 다음이 성립한다.

nullity⁡(T⁡)+rank⁡(T⁡)=dim⁡(V) \operatorname{nullity}(\operatorname{T})+\operatorname{rank}(\operatorname{T})= \dim(\mathbf{V} )

  • 직관적으로 선형변환에서 nullity 가 커질수록 랭크는 작아진다. 즉, 더 많은 벡터가 영벡터 00 로 갈수록 상공간은 작아진다. 역으로 랭크가 커질수록 nullity 는 작아진다. 이 정리가 랭크과 nullity 의 관계를 말해준다.

  • 증명

    dim⁡(V)=n,dim⁡(ker⁡(T⁡))=k\dim(\mathbf{V} ) = n, \dim(\ker(\operatorname{T} )) = k 라 하고 ker⁡(T⁡)\ker(\operatorname{T} ) 의 기저를 {v1,v2,…,vk}\{v_1, v_2, \dots, v_k\} 라 하면 정리 1.11 따름정리 에 의하여 {v1,v2,…,vk}\{v_1, v_2, \dots, v_k\} 를 확장하여 V\mathbf{V} 의 기저 β={v1,v2,…,vn}\beta = \{v_1, v_2, \dots, v_n\} 을 얻을 수 있다. ▲

    그러면

    S=T⁡(β−{v1,…,vk})={T⁡(vk+1),T⁡(vk+2),…,T⁡(vn)}S = \operatorname{T} (\beta - \{v_1, \dots, v_k\}) = \{\operatorname{T} (v _{k+1}), \operatorname{T} (v _{k+2}), \dots, \operatorname{T} (v _{n})\}

    이 im⁡(T⁡)\operatorname{im}(\operatorname{T} ) 의 기저임을 보이자. 먼저 span⁡(S)=im⁡(T⁡)\operatorname{span}(S) = \operatorname{im}(\operatorname{T} ) 임을 보이기 위하여 1≤i≤k:T⁡(vi)=01 \leq i \leq k : \operatorname{T} (v_i) = 0 과 정리 2.2 를 사용하면

    im⁡(T⁡)=span⁡({T⁡(v1),T⁡(v2),…,T⁡(vn)})=span⁡({T⁡(vk+1),T⁡(vk+2),…,T⁡(vn)})=span⁡(S) \begin{align}\begin{split} \operatorname{im}(\operatorname{T} ) &= \operatorname{span}(\{\operatorname{T} (v_1), \operatorname{T} (v_2), \dots, \operatorname{T} (v_n)\}) \\ &= \operatorname{span}(\{\operatorname{T} (v _{k+1}), \operatorname{T} (v _{k+2}), \dots, \operatorname{T} (v_n)\}) = \operatorname{span}(S) \\ \end{split}\end{align}\tag*{}

    이다. ▲

    SS 가 선형독립임을 보이기 위하여 bk+1,…,bn∈Fb _{k+1}, \dots, b _{n} \in \mathbf{F} 에 대하여 ∑i=k+1nbiT⁡(vi)=0\displaystyle \sum_{i=k+1}^{n}b_i \operatorname{T} (v_i) = 0 라고 하면 T⁡\operatorname{T} 가 선형이므로

    T⁡(∑i=k+1nbivi)=0⟺∑i=k+1nbivi∈ker⁡(T⁡) \operatorname{T} \bigg (\sum_{i=k+1}^{n}b_iv_i\bigg ) = 0 \iff \sum_{i=k+1}^{n}b_iv_i \in \ker(\operatorname{T} )

    이다. 그러면 다음 식을 만족하는 c1,…,ck∈Fc_1, \dots, c_k \in \mathbf{F} 가 존재한다.

    ∑i=k+1nbivi=∑i=1kcivi⟺∑i=1k(−ci)vi+∑i=k+1nbivi=0 \sum_{i=k+1}^{n}b_iv_i = \sum_{i=1}^{k}c_iv_i \iff \sum_{i=1}^{k}(-c_i)v_i + \sum_{i=k+1}^{n}b_iv_i = 0

    이때 β\beta 가 기저, 즉 일차독립이므로 이 식이 성립하려면 반드시 −c1=⋯=−ck=bk+1=⋯=bn=0-c_1 = \dots = -c_k = b _{k+1} = \dots = b_n = 0 이어야 한다. 그러므로 SS 는 일차독립이다. 그러므로 SS 는 im⁡(T⁡)\operatorname{im}(\operatorname{T} ) 의 기저이다. ▲

    S=T⁡(β−{v1,…,vk})S = \operatorname{T} (\beta - \{v_1, \dots, v_k\}) 가 im⁡(T⁡)\operatorname{im}(\operatorname{T} ) 의 기저이므로 T⁡\operatorname{T} 는 최소한

    ∣{vk+1,…,vn}∣=∣{T⁡(vk+1),…,T⁡(vn)}∣ |\{v _{k+1}, \dots, v_n\}| = |\{\operatorname{T} (v _{k+1}) , \dots, \operatorname{T} (v_n)\}|

    을 보장한다. 그러므로 ∣S∣=∣β∣−∣{v1,…,vk}∣|S| = |\beta | - |\{v_1, \dots, v_k\}| 라고 할 수 있고, 이에 따라

    ∴rank⁡(T⁡)=dim⁡(V)−nullity⁡(T⁡) \therefore \operatorname{rank}(\operatorname{T} ) = \dim(\mathbf{V} ) - \operatorname{nullity}(\operatorname{T} )

    이다. ■

Properties of Linear Map, Range, Null Space✔

정리 2.4

벡터공간 V,W\mathbf{V} , \mathbf{W} 와 선형변환 T⁡:V→W\operatorname{T} : \mathbf{V} \to \mathbf{W} 에 대하여 다음은 동치이다.

  1. T⁡\operatorname{T} 가 단사사상이다.

  2. ker⁡(T⁡)={0}\ker(\operatorname{T} ) = \{0\}

  • 증명

    x∈ker⁡(T⁡)x \in \ker(\operatorname{T} ) 이면 T⁡(x)=0=T⁡(0)\operatorname{T} (x) = 0 = \operatorname{T} (0) 인데, T⁡\operatorname{T} 가 단사이므로 x=0x = 0 이다. 또한 이는 ∀x∈ker⁡(T⁡):x=0\forall x \in \ker(\operatorname{T} ) : x = 0 을 의미하므로 ker⁡(T⁡)={0}\ker(\operatorname{T} ) = \{0\} 이다. ▲

    역으로 ker⁡(T⁡)={0}\ker(\operatorname{T} ) = \{0\} 과 T⁡(x)=T⁡(y)\operatorname{T} (x) = \operatorname{T} (y) 을 가정하자. 선형변환의 성질 3) 에 의하여 0=T⁡(x)−T⁡(y)=T⁡(x−y)0 = \operatorname{T} (x) - \operatorname{T} (y) = \operatorname{T} (x - y) 이므로

    x−y∈ker⁡(T⁡)={0}⟺x−y=0 x - y \in \ker(\operatorname{T} ) = \{0\} \iff x - y = 0

    이다. 즉, x=yx = y 이므로 T⁡\operatorname{T} 는 단사함수이다. ■

정리 2.5

유한차원 벡터공간 V,W\mathbf{V} ,\mathbf{W} 에 대하여 dim⁡(V)=dim⁡(W)\dim(\mathbf{V} ) = \dim(\mathbf{W} ) 이면 선형변환 T⁡:V→W\operatorname{T} : \mathbf{V} \to \mathbf{W} 에 대하여 다음 명제가 동치이다.

  1. T⁡\operatorname{T} 는 단사이다.

  2. T⁡\operatorname{T} 는 전사이다.

  3. rank⁡(T⁡)=dim⁡(V)\operatorname{rank}(\operatorname{T} ) = \dim(\mathbf{V} )

  • 이 정리는 차원이 같은 유한차원 사이의 선형사상이 단사이면 전단사임을 말해준다. 그러나 무한차원 V\mathbf{V} 에 대한 선형사상 T⁡:V→V\operatorname{T} : \mathbf{V} \to \mathbf{V} 에 대해서는 단사와 전사가 동치가 아니다.

  • 증명

    차원정리 에 의하여 rank⁡(T⁡)+nullity⁡(T⁡)=dim⁡(V)\operatorname{rank}(\operatorname{T} )+\operatorname{nullity}(\operatorname{T} ) = \dim(\mathbf{V} ) 인데, 정리 2.4 에 의하여

    T⁡ is injection ⟺ker⁡(T⁡)={0} \operatorname{T} \text{ is injection } \iff \ker(\operatorname{T} ) = \{0\}
    ⟺nullity⁡(T⁡)=0⟺rank⁡(T⁡)=dim⁡(V) \iff \operatorname{nullity}(\operatorname{T} ) = 0 \iff \operatorname{rank}(\operatorname{T} ) = \dim(\mathbf{V} )
    ⟺rank⁡(T⁡)=dim⁡(W)⟺dim⁡(im⁡(T⁡))=dim⁡(W) \iff \operatorname{rank}(\operatorname{T} ) = \dim(\mathbf{W} ) \iff \dim(\operatorname{im}(\operatorname{T} )) = \dim(\mathbf{W} )

    이다. 그런데 정리 1.11 에 의하여

    ⟺im⁡(T⁡)=W \iff \operatorname{im}(\operatorname{T} ) = \mathbf{W}

    이다. 상공간과 공역이 같으므로 T⁡\operatorname{T} 는 전사이다. ■

  • 예시

    선형변환 T⁡:F2→F2\operatorname{T} : \mathbf{F} ^{2} \to \mathbf{F} ^{2} 이

    T⁡(v,w)=(v+w,v) \operatorname{T} (v, w) = (v+w, v)

    와 같이 정의되면 ker⁡(T⁡)={0}\ker(\operatorname{T} ) = \{0\} 이므로 T⁡\operatorname{T} 는 전단사이다.

벡터공간 V,W\mathbf{V} ,\mathbf{W} 의 선형변환 T⁡:V→W\operatorname{T} : \mathbf{V} \to \mathbf{W} 과 V\mathbf{V} 의 부분집합 SS 에 대하여 다음이 동치이다.

  1. SS 가 일차독립이다.

  2. T⁡(S)\operatorname{T} (S) 가 일차독립이다.

  • 증명

  • 예시

    선형변환 T⁡:P2(R)→R3\operatorname{T} : \mathbf{P} _2(\R) \to \R ^{3} 이

    T⁡(a0+a1x+a2x2)=(a0,a1,a2) \operatorname{T} (a_0+a_1x+a_2x ^{2}) = (a_0, a_1, a_2)

    와 같이 정의되면 T⁡\operatorname{T} 는 단사이다. S={2−x+3x2,x+x2,1−2x2}S = \{2-x+3x ^{2}, x+x ^{2}, 1-2x ^{2}\} 라고 하면 T⁡(S)={(2,−1,3),(0,1,1),(1,0,−2)}\operatorname{T} (S) = \{(2,-1,3), (0,1,1), (1,0,-2)\} 가 R3\R ^{3} 에서 일차독립이므로 SS 도 일차독립이다.

정리 2.6

F\mathbf{F}-벡터공간 V,W\mathbf{V} , \mathbf{W} 와 V\mathbf{V} 의 기저 {v1,…,vn}\{v_1, \dots, v_n\} 와 벡터 w1,…,wn∈Ww_1, \dots, w_n \in \mathbf{W} 에 대하여

i∈{1,2,…,n}:T⁡(vi)=wi i \in \{1,2,\dots, n\} : \operatorname{T} (v_i) = w_i

을 만족하는 선형변환 T⁡:V→W\operatorname{T} : \mathbf{V} \to \mathbf{W} 가 유일하게 존재한다.

  • 이 정리는 선형변환이 기저에 따라 어떻게 행동할지 완벽하게 결정된다는 것을 말해준다. 이 정리와 따름정리는 매우 중요해서 선형대수학 전반에 널리 사용된다.

  • 증명

    x∈Vx \in \mathbf{V} 를 다음과 같이 a1,…,an∈Fa_1, \dots, a_n \in \mathbf{F} 에 대하여 기저의 유일한 일차결합 표현으로 나타낼 수 있다.

    x=∑i=1naivi x = \sum_{i=1}^{n}a_iv_i

    이때 선형변환 T⁡:V→W\operatorname{T} : \mathbf{V} \to \mathbf{W} 를 T⁡(x)=∑i=1naiwi\operatorname{T} (x) = \sum_{i=1}^{n} a_iw_i 로 정의하자. ▲

    그리고 먼저 T⁡\operatorname{T} 가 선형임을 보이자. u,v∈V,d∈Fu, v \in \mathbf{V} , d \in \mathbf{F} 와 b1,…,bn∈Fb_1, \dots, b_n \in \mathbf{F} 와 c1,…,cn∈Fc_1, \dots, c_n \in \mathbf{F} 에 대하여

    u=∑i=1nbivi,v=∑i=1ncivi u = \sum_{i=1}^{n}b_iv_i, \enspace v = \sum_{i=1}^{n}c_iv_i

    이다. 그러면 du+v=∑i=1n(dbi+ci)vidu + v = \sum_{i=1}^{n} (db_i+c_i)v_i 이므로

    T⁡(du+v)=∑i=1n(dbi+ci)wi=d∑i=1nbiwi+∑i=1nciwi=dT⁡(u)+T⁡(v) \operatorname{T} (du+v) = \sum_{i=1}^{n}(db_i+c_i)w_i = d \sum_{i=1}^{n}b_iw_i + \sum_{i=1}^{n}c_iw_i = d \operatorname{T} (u) + \operatorname{T} (v)

    이다. ▲

    또한 정의에 의하여 i∈{1,…,n}:T⁡(vi)=wii \in \{1, \dots, n\} : \operatorname{T} (v_i) = w_i 이다. ▲

    마지막으로 T⁡\operatorname{T} 의 유일성을 보이자. 선형변환 U⁡:V→W\operatorname{U}:\mathbf{V} \to \mathbf{W} 가 i∈{1,…,n}:T⁡(vi)=wii \in \{1, \dots, n\} : \operatorname{T} (v_i) = w_i 를 만족한다고 하면 x=∑i=1naivi∈Vx = \sum_{i=1}^{n}a_iv_i \in \mathbf{V} 에 대하여

    U⁡(x)=∑i=1naiU⁡(vi)=∑i=1naiwi=T⁡(x) \operatorname{U} (x) = \sum_{i=1}^{n}a_i \operatorname{U} (v_i) = \sum_{i=1}^{n}a_iw_i = \operatorname{T} (x)

    이므로 U⁡=T⁡\operatorname{U} =\operatorname{T} 이다. ■

정리 2.6 따름정리

벡터공간 V,W\mathbf{V} , \mathbf{W} 에 대하여 V\mathbf{V} 가 유한집합 기저 {v1,…,vn}\{v_1, \dots, v_n\} 을 가지면 두 선형변환 U⁡,T⁡:V→W\operatorname{U} , \operatorname{T} : \mathbf{V} \to \mathbf{W} 에 대하여 다음이 성립한다.

i∈{1,…,n}:U⁡(vi)=T⁡(vi)⟹U⁡=T⁡ i \in \{1, \dots, n\} : \operatorname{U} (v_i) = \operatorname{T} (v_i) \implies \operatorname{U} = \operatorname{T}

  • 이 정리는 두 선형변환이 기저에서 상이 같으면 같은 선형변환임을 말하고 있다.

  • 예시

    선형변환 T⁡:R2→R2\operatorname{T} :\R ^{2} \to \R ^{2} 이

    T⁡(a1,a2)=(2a2−a1,3a1) \operatorname{T} (a_1, a_2) = (2a_2 - a_1, 3a_1)

    와 같이 정의되었다고 하자. 그러면 {(1,2),(1,1)}\{(1,2), (1,1)\} 이 R2\R ^{2} 의 기저이므로 선형변환 U⁡:R2→R2\operatorname{U} : \R ^{2} \to \R ^{2} 이 U⁡(1,2)=(3,3),U⁡(1,1)=(1,3)\operatorname{U} (1,2)=(3,3), \operatorname{U} (1,1)=(1,3) 이면 U⁡=T⁡\operatorname{U} =\operatorname{T} 이다.

Coordinate Vector✔

순서기저(ordered basis)

유한차원 벡터공간의 순서가 주어진 기저이다.

  • 즉, 순서기저란 일차독립이고 벡터공간을 생성하는 수열이다.

  • 예시

    F3\mathbf{F} ^{3} 에서 β={e1,e2,e3},γ={e2,e1,e3}\beta = \{e_1, e_2, e_3\}, \gamma = \{e_2, e_1, e_3\} 은 순서기저이다. 순서기저의 관점에서 β≠γ\beta \neq \gamma 이다.

  • 표준기저와 마찬가지로 표준순서기저(standard ordered basis)도 정의할 수 있다.

  • 예시

    벡터공간 Fn\mathbf{F} ^{n} 에서 {e1,e2,…,en}\{e_1, e_2, \dots, e_n\} 을 표준순서기저라고 한다.

    벡터공간 Pn(F)\mathbf{P}_n(\mathbf{F} ) 에서 {1,x,…,xn}\{1, x, \dots, x ^{n}\} 이 표준순서기자이다.

좌표벡터(coordinate vector)

유한차원 벡터공간 V\mathbf{V} 의 순서기저 β={u1,u2,…,un}\beta = \{u_1, u_2, \dots, u_n\} 와 벡터 x∈Vx \in \mathbf{V} 에 대하여 x=∑i=1naiuix = \displaystyle \sum_{i=1}^{n}a_iu_i 을 만족하는 유일한 스칼라 a1,a2,…,ana_1, a_2, \dots, a_n 가 존재한다. 이때 β\beta 에 대한 xx 의 좌표벡터 [x]β[x] _{\beta } 를 다음과 같이 정의한다.

[x]β=(a1a2⋮an) [x] _{\beta } = \begin{pmatrix} a_1\\ a_2\\ \vdots\\ a_n \end{pmatrix}

  • [x]β[x] _{\beta } 를 xx 라는 벡터를 기저 β\beta 의 일차결합으로 나타낸 것의 coefficient matrix 라고 생각하면 편하다.

  • 변환 V→Fn,x↦[x]β\mathbf{V} \to \mathbf{F} ^{n}, x \mapsto [x] _{\beta } 는 선형변환이다.

  • 예시

    순서기저 β={1,x,x2}\beta = \{1, x, x ^{2}\} 를 가지는 벡터공간 V=P2(R)\mathbf{V} = \mathbf{P} _2 (\R) 에 대하여 다음이 성립한다.

    f(x)=4+6x−7x2⟺[f]β=(46−7) f(x) = 4+6x-7x ^{2} \iff [f] _{\beta } = \begin{pmatrix} 4\\ 6\\ -7\\ \end{pmatrix}

  • 예시

    표준순서기저를 순서기저 β\beta 로 갖는 벡터공간 R3\R ^{3} 에 대하여 벡터 x∈R3x \in \R ^{3} 가 x=(−100,2,50)x = (-100, 2, 50) 이라면

    x=−100e1+2e2+50e3 x = -100 e_1 + 2 e_2 + 50 e_3

    이므로 다음이 성립한다.

    [x]β=(−100250) [x] _{\beta } = \begin{pmatrix} -100\\ 2\\ 50\\ \end{pmatrix}

  • 예시

    다음과 같이 똑같은 벡터도 다른 좌표 시스템에서는 다른 좌표를 갖게 된다.

벡터공간 Fn\mathbf{F} ^{n} 와 표준순서기저 β={e1,e2,…,en}\beta = \{e_1, e_2, \dots, e_n\} 와 벡터 x∈Fnx \in \mathbf{F} ^{n} 에 대하여 다음이 성립한다.

[x]β=x [x] _{\beta} = x

  • 이는 어떤 벡터의 좌표벡터를 표준순서기저로 나타낸다면 그 결과가 결국 본래의 벡터라는 것을 말해준다.

  • 증명

    x=(x1x2⋮xn)=x1e1+x2e2+⋯+xnen=∑i=1nxiei⟹[x]β=(x1x2⋮xn)■ x = \begin{pmatrix} x_1\\ x_2\\ \vdots \\ x_n\\ \end{pmatrix} = x_1 e_1 + x_2 e_2 + \dots + x_n e_n = \sum_{i=1}^{n}x_ie_i \implies [x] _{\beta } = \begin{pmatrix} x_1\\ x_2\\ \vdots \\ x_n\\ \end{pmatrix} \tag*{■}

Matrix Representation of Linear Map✔

선형변환의 행렬표현(matrix representation)

유한차원 벡터공간 V,W\mathbf{V} , \mathbf{W} 의 각각의 순서기저 β={v1,…,vn},γ={w1,…,wm}\beta = \{v_1, \dots, v_n\}, \gamma = \{w_1, \dots, w_m\} 에 대하여 선형변환 T⁡:V→W\operatorname{T} : \mathbf{V} \to \mathbf{W} 을 정의하면 j∈{1,…,n},i∈{1,…,m}j \in \{1,\dots,n\}, i \in \{1, \dots, m\} 에 대하여

T⁡(vj)=∑i=1maijwi \operatorname{T} (v_j) = \sum_{i=1}^{m}a _{ij}w_i

을 만족하는 유일한 스칼라 aij∈Fa _{ij}\in \mathbf{F} 가 존재한다. 성분이 Aij=aijA _{ij} = a _{ij} 인 m×nm \times n 행렬 AA 를 순서기저 β,γ\beta , \gamma 에 대한 선형변환 T⁡\operatorname{T} 의 행렬표현

A=[T⁡]βγ \boxed{A = [\operatorname{T} ] ^{\gamma } _{\beta } }

라 한다.

  • 스칼라 aija _{ij} 의 유일성은 정리 1.8 이 보장해준다.

  • 우리는 이렇게 행렬과 선형변환을 연결했는데, 정리 2.8 은 이 연결이 합과 스칼라 곱을 보존함을 말해준다. 이를 위해 먼저 선형변환의 합과 스칼라 곱을 정의해볼 것이다.

  • V=W∧β=γ\mathbf{V} = \mathbf{W} \land \beta = \gamma 이면 간단하게 A=[T⁡]βA = [\operatorname{T} ]_{\beta } 라고 표기한다.

  • AA 의 jj 열은 [T⁡(vj)]γ[\operatorname{T} (v_j)] _{\gamma } 이다.

  • 선형변환 U⁡:V→W\operatorname{U} : \mathbf{V} \to \mathbf{W} 가 [U⁡]βγ=[T⁡]βγ[\operatorname{U} ] ^{\gamma } _{\beta } = [\operatorname{T} ]^{\gamma }_{\beta } 를 만족하면 정리 2.6 따름정리 에 의하여 U⁡=T⁡\operatorname{U} = \operatorname{T} 이다.

  • 예시

    선형변환 T⁡:R2→R3,(a1,a2)↦(a1+3a2,0,2a1−4a2)\operatorname{T} : \R ^{2} \to \R ^{3} , (a_1, a_2) \mapsto (a_1 + 3a_2, 0, 2a_1 - 4a_2) 를 정의하고 R2,R3\R ^{2}, \R ^{3} 의 순서기저 β,γ\beta , \gamma 를 각각의 표준순서기저로 두면

    T⁡(1,0)=(1,0,2)=1e1+0e2+2e3 \operatorname{T} (1, 0) = (1, 0, 2) = 1e_1 + 0e_2 + 2e_3
    T⁡(0,1)=(3,0,−4)=3e1+0e2−4e3 \operatorname{T} (0, 1) = (3, 0, -4) = 3e_1 + 0e_2 - 4e_3

    가 성립하므로

    [T⁡]βγ=(13002−4) [\operatorname{T} ]^{\gamma } _{\beta } = \begin{pmatrix} 1&3\\ 0&0\\ 2&-4\\ \end{pmatrix}

    이다. 만약 R3\R ^{3} 의 순서기저로써 γ′={e3,e2,e1}\gamma ' = \{e_3, e_2, e_1\} 를 가져오면 다음과 같이 된다.

    [T⁡]βγ′=(2−40013) [\operatorname{T} ] ^{\gamma '} _{\beta } =\begin{pmatrix} 2&-4\\ 0&0\\ 1&3\\ \end{pmatrix}

  • 예시

    선형변환 T⁡:P3(R)→P2(R)\operatorname{T} : \mathbf{P} _3(\R) \to \mathbf{P} _2(\R) 가 T⁡(f(x))=f′(x)\operatorname{T} (f(x)) = f'(x) 와 같이 정의되었고, P3(R),P2(R)\mathbf{P} _3(\R), \mathbf{P} _2(\R) 의 순서기저 β,γ\beta , \gamma 를 표준순서기저라 하면

    T⁡(1)=0⋅1+0⋅x+0⋅x2 \operatorname{T} (1) = 0 \cdot 1 + 0 \cdot x + 0 \cdot x ^{2}
    T⁡(x)=1⋅1+0⋅x+0⋅x2 \operatorname{T} (x) = 1 \cdot 1 + 0 \cdot x + 0 \cdot x ^{2}
    T⁡(x2)=0⋅1+2⋅x+0⋅x2 \operatorname{T} (x ^{2}) = 0 \cdot 1 + 2 \cdot x + 0 \cdot x ^{2}
    T⁡(x3)=0⋅1+0⋅x+3⋅x2 \operatorname{T} (x ^{3}) = 0 \cdot 1 + 0 \cdot x + 3 \cdot x ^{2}

    이 성립하므로 다음이 성립한다.

    [T⁡]βγ=(010000200003) [\operatorname{T} ]^{\gamma } _{\beta } = \begin{pmatrix} 0&1&0&0\\ 0&0&2&0\\ 0&0&0&3\\ \end{pmatrix}

영변환의 행렬표현은 영행렬이다.

  • 예시

    유한차원 벡터공간 V,W\mathbf{V} , \mathbf{W} 의 순서기저를 β={v1,…,vn},γ={w1,…,wm}\beta = \{v_1, \dots, v_n\}, \gamma = \{w_1, \dots, w_m\} 이라 하면

    T⁡0(vj)=0=0w1+⋯+0wm \operatorname{T} _0(v_j) = 0 = 0w_1+\dots+0w_m

    이므로 [T⁡0]βγ=O[\operatorname{T} _0] ^{\gamma } _{\beta } = O 이다. OO 는 m×nm \times n 영행렬이다.

항등변환의 행렬표현은 항등행렬이다.

  • 예시

    유한차원 벡터공간 V\mathbf{V} 의 순서기저를 β={v1,…,vn}\beta = \{v_1, \dots, v_n\} 이라 하면

    I⁡V(vj)=vj=0v1+⋯+0vj−1+1vj+0vj+1⋯+0vn \operatorname{I} _{\mathbf{V} }(v_j) = v_j = 0v_1 + \dots + 0v _{j-1} + 1v_j+ 0 v _{j+1} \dots + 0 v_n

    이므로 I⁡V\operatorname{I} _{\mathbf{V} } 의 jj 열은 eje_j 이다. 따라서

    [I⁡V]β=(10…001…0⋮⋮⋱⋮00…1)=In [\operatorname{I} _{\mathbf{V} }]_{\beta } = \begin{pmatrix} 1&0&\dots&0\\ 0&1&\dots&0\\ \vdots & \vdots & \ddots & \vdots \\ 0&0&\dots&1\\ \end{pmatrix} = I_n

    이다. [I⁡V]β[\operatorname{I} _{\mathbf{V} }]_{\beta } 는 n×nn \times n 항등행렬 InI_n 이다.

문제 2.2-12

벡터공간 V\mathbf{V} 의 순서기저 β={v1,v2,…,vn}\beta = \{v_1, v_2, \dots, v_n\} 와 선형연산자 T⁡\operatorname{T} 와 j∈{1,…,n}j \in \{1, \dots, n\} 에 대하여 [T⁡]β[\operatorname{T}]_{\beta } 가 상삼각행렬인 것과 T⁡(vj)∈span⁡({v1,v2,…,vj})\operatorname{T}(v_j) \in \operatorname{span} (\{v_1, v_2, \dots, v_j\}) 인 것은 동치이다.

  • 증명

    [T⁡]β[\operatorname{T}]_{\beta } 가 상삼각행렬이면 다음이 성립한다.

    T⁡(vj)=∑i=1jaijvi∈span⁡({v1,v2,…,vj})▲ \operatorname{T}(v_j) = \sum_{i=1}^{j}a _{ij}v_i \in \operatorname{span} (\{v_1, v_2, \dots, v_j\}) \tag*{▲}

    T⁡(vj)∈span⁡({v1,v2,…,vj})\operatorname{T}(v_j) \in \operatorname{span} (\{v_1, v_2, \dots, v_j\}) 를 가정하면 다음이 성립한다.

    T⁡(vj)=∑i=1jaijvi \operatorname{T}(v_j) = \sum_{i=1}^{j}a _{ij}v_i

    따라서 [T⁡]β[\operatorname{T}]_{\beta } 는 상삼각행렬이다. ■

Kronecker delta✔

크로네커 델타(Kronecker delta)

δij={1i=j0i≠j\delta _{ij} = \begin{cases} 1 & i = j\\ 0 & i \neq j\\ \end{cases}

  • 예시

    n×nn \times n 항등행렬 InI_n 의 성분은 (In)ij=δij(I_n) _{ij} = \delta _{ij} 이다.

Addition, Multiples of Linear Maps✔

F\mathbf{F}-벡터공간 V,W\mathbf{V} , \mathbf{W} 에서 정의된 임의의 함수 T⁡,U⁡:V→W\operatorname{T} , \operatorname{U} : \mathbf{V} \to \mathbf{W} 와 a∈Fa \in \mathbf{F} 와 ∀x∈V\forall x \in \mathbf{V} 에 대하여 두 함수의 합과 스칼라곱을 다음과 같이 정의한다.

  • T⁡+U⁡:V→W,(T⁡+U⁡)(x)=T⁡(x)+U⁡(x)\operatorname{T} + \operatorname{U} : \mathbf{V} \to \mathbf{W}, (\operatorname{T} + \operatorname{U} )(x) = \operatorname{T} (x) + \operatorname{U} (x)

  • aT⁡:V→W,(aT⁡)(x)=aT⁡(x)a \operatorname{T} : \mathbf{V} \to \mathbf{W}, (a \operatorname{T} )(x) = a \operatorname{T} (x)
  • 이는 함수의 합의 스칼라 곱에 대한 보편적 정의인데 선형변환의 합과 스칼라 곱이 여전히 선형임을 다음 정리가 말해준다.

Set of All Linear Maps is Vector Space✔

정리 2.7

F\mathbf{F}-벡터공간 V,W\mathbf{V} , \mathbf{W} 와 선형변환 T⁡,U⁡:V→W\operatorname{T} , \operatorname{U} : \mathbf{V} \to \mathbf{W} 에 대하여 다음이 성립한다.

  1. ∀a∈F\forall a \in \mathbf{F} 에 대하여 aT⁡+U⁡a \operatorname{T} + \operatorname{U} 은 선형이다.

  2. V→W\mathbf{V} \to \mathbf{W} 에서 정의된 모든 선형변환의 집합은 F\mathbf{F}-벡터공간이다.

  • 증명

    1:

    x,y∈V,c∈Fx, y \in \mathbf{V} , c \in \mathbf{F} 에 대하여 다음이 성립한다.

    (aT⁡+U⁡)(cx+y)=aT⁡(cx+y)+U⁡(cx+y)=a[T⁡(cx+y)]+cU⁡(x)+U⁡(y)=a[cT⁡(x)+T⁡(y)]+cU⁡(x)+U⁡(y)=acT⁡(x)+cU⁡(x)+aT⁡(y)+U⁡(y)=c(aT⁡+U⁡)(x)+(aT⁡+U⁡)(y) \begin{align}\begin{split} (a \operatorname{T} + \operatorname{U} )(cx+y)&=a \operatorname{T} (cx+y) + \operatorname{U} (cx + y)\\ &=a[\operatorname{T} (cx+y)] + c \operatorname{U} (x) + \operatorname{U} (y)\\ &=a[c\operatorname{T} (x) + \operatorname{T}(y)] + c \operatorname{U} (x) + \operatorname{U} (y)\\ &=ac\operatorname{T} (x) + c\operatorname{U}(x) + a \operatorname{T} (y) + \operatorname{U} (y)\\ &=c(a\operatorname{T} + \operatorname{U} ) (x) + (a \operatorname{T} + \operatorname{U} )(y)\\ \end{split}\end{align}\tag*{}

    그러므로 aT⁡+U⁡a \operatorname{T} + \operatorname{U} 는 선형이다. ■

    2:

    위의 정의는 임의의 함수에 대한 두 함수의 합, 스칼라 곱을 정의한 것이므로 선형변환의 합과 스칼라곱에도 적용된다. 그러므로 이 합과 스칼라 곱을 만족하는 선형변환 집합이 벡터공간의 조건을 만족하는지 확인하면 된다.

    V→W\mathbf{V} \to \mathbf{W} 에서 정의된 모든 선형변환의 집합을 L\mathcal{L} 라고 하자. 그러면 영변환 L⁡0:V→W\operatorname{L} _0: \mathbf{V} \to \mathbf{W} 는 L\mathcal{L} 에서 영벡터의 역할을 한다. 또한 L\mathcal{L} 가 벡터공간의 8 가지 조건을 만족한다는 것을 쉽게 확인할 수 있다.

    그러므로 L\mathcal{L} 는 F\mathbf{F}-벡터공간이다. ■

벡터공간 L(V,W)\mathcal{L}(\mathbf{V} , \mathbf{W} )

벡터공간 L(V,W)\mathcal{L}(\mathbf{V} , \mathbf{W} ) 은 F\mathbf{F}-벡터공간 V,W\mathbf{V} , \mathbf{W} 에 대하여 V→W\mathbf{V} \to \mathbf{W} 에서 정의된 모든 선형변환의 집합이다.

  • V=W\mathbf{V} = \mathbf{W} 이면 간단하게 L(V)\mathcal{L}(\mathbf{V} ) 라 표기한다.

  • 참고로 2.4 절에서 차원 dim⁡(V)=n,dim⁡(W)=m\dim(\mathbf{V} ) = n, \dim(\mathbf{W} ) = m 인 벡터공간 V,W\mathbf{V} , \mathbf{W} 에 대하여 L(V,W)\mathcal{L}(\mathbf{V} , \mathbf{W} ) 와 Fm×n\mathbf{F}^{m \times n} 가 본질적으로 같다는 것을 보일 것이다.

정리 2.8

체 F\mathbf{F} 에 대한 유한차원 F\mathbf{F}-벡터공간 V,W\mathbf{V} , \mathbf{W} 와 각각의 순서기저 β,γ\beta , \gamma 와 선형변환 T⁡,U⁡:V→W\operatorname{T} , \operatorname{U} : \mathbf{V} \to \mathbf{W} 에 대하여 다음이 성립한다.

  1. [T⁡+U⁡]βγ=[T⁡]βγ+[U⁡]βγ[\operatorname{T} + \operatorname{U} ] ^{\gamma } _{\beta } = [\operatorname{T} ] ^{\gamma } _{\beta } + [\operatorname{U} ] ^{\gamma } _{\beta }

  2. ∀a∈F:[aT⁡]βγ=a[T⁡]βγ\forall a \in \mathbf{F} :[a \operatorname{T} ] ^{\gamma } _{\beta } = a[ \operatorname{T} ] ^{\gamma } _{\beta }

  • 증명

    β={v1,…,vn},γ={w1,…,wm}\beta = \{v_1, \dots, v_n\}, \gamma = \{w_1, \dots, w_m\} 에 대하여

    T⁡(vj)=∑i=1maijwi,U⁡(vj)=∑i=1mbijwi,j∈{1,…,n} \operatorname{T} (v_j) = \sum_{i=1}^{m}a _{ij}w_i, \enspace \operatorname{U} (v_j) = \sum_{i=1}^{m}b _{ij}w_i, \qquad j \in \{1, \dots, n\}

    을 만족하는 유일한 스칼라 aij,bij(i≤i≤m,1≤j≤n)a _{ij}, b _{ij} \enspace (i \leq i \leq m, 1 \leq j \leq n) 가 존재한다. 즉,

    (T⁡+U⁡)(vj)=∑i=1m(aij+bij)wi (\operatorname{T} + \operatorname{U} ) (v_j) = \sum_{i=1}^{m}(a _{ij} + b _{ij}) w_i

    이고

    ([T⁡+U⁡]βγ)ij=aij+bij=([T⁡]βγ+[U⁡]βγ)ij ([\operatorname{T} + \operatorname{U} ] ^{\gamma } _{\beta }) _{ij} = a _{ij} + b _{ij} = ([\operatorname{T} ] ^{\gamma } _{\beta } + [\operatorname{U} ] ^{\gamma } _{\beta }) _{ij}

    이다. ▲

    두번째도 행렬의 원소가 같다는 것을 보이는 방식으로 증명가능하다. ■

  • 예시

    선형변환 T⁡:R2→R3,U⁡:R2→R3\operatorname{T} : \R ^{2} \to \R ^{3}, \operatorname{U} : \R ^{2} \to \R ^{3} 을

    T⁡(a1,a2)=(a1+3a2,0,2a1−4a2),U⁡(a1,a2)=(a1−a2,2a1,3a1+2a2) \operatorname{T} (a_1, a_2) = (a_1 + 3a_2, 0, 2a_1 - 4a_2), \enspace \operatorname{U} (a_1, a_2) = (a_1 - a_2, 2a_1, 3a_1 + 2a_2)

    와 같이 정의하고, R2,R3\R ^{2}, \R ^{3} 의 순서기저로써 각각의 표준순서기저 β,γ\beta , \gamma 를 두면

    T⁡(1,0)=(1,0,2)=1e1+0e2+2e3 \operatorname{T} (1, 0) = (1, 0, 2) = 1e_1 + 0e_2 + 2e_3
    T⁡(0,1)=(3,0,−4)=3e1+0e2+−4e3 \operatorname{T} (0, 1) = (3, 0, -4) = 3e_1 + 0e_2 + -4e_3

    이고, U⁡\operatorname{U} 의 경우도 표준순서기저의 일차결합의 스칼라를 구해보면

    [T⁡]βγ=(13002−4),[U⁡]βγ=(1−12032) [\operatorname{T} ] ^{\gamma } _{\beta } = \begin{pmatrix} 1&3\\ 0&0\\ 2&-4\\ \end{pmatrix}, [\operatorname{U} ] ^{\gamma } _{\beta } = \begin{pmatrix} 1&-1\\ 2&0\\ 3&2\\ \end{pmatrix}

    이 성립한다. ▲

    T⁡+U⁡\operatorname{T} + \operatorname{U} 는 정의에 따라

    (T⁡+U⁡)(a1,a2)=(2a1+2a2,2a1,5a1−2a2) (\operatorname{T} + \operatorname{U} )(a_1, a_2) = (2a_1 + 2a_2, 2a_1, 5a_1 - 2a_2)

    이다. 그러면

    (T⁡+U⁡)(1,0)=(2,2,5)=2e1+2e2+5e3 (\operatorname{T} + \operatorname{U} )(1, 0) = (2, 2, 5) = 2e_1 + 2e_2 + 5e_3
    (T⁡+U⁡)(0,1)=(2,0,−2)=2e1+0e2−2e3 (\operatorname{T} + \operatorname{U} )(0, 1) = (2, 0, -2) = 2e_1 + 0e_2 - 2e_3

    이므로

    [T⁡+U⁡]βγ=(22205−2) [\operatorname{T} + \operatorname{U} ] ^{\gamma } _{\beta } = \begin{pmatrix} 2&2\\ 2&0\\ 5&-2\\ \end{pmatrix}

    이다. 그러므로 [T⁡+U⁡]βγ=[T⁡]βγ+[U⁡]βγ[\operatorname{T} + \operatorname{U} ] ^{\gamma}_{\beta} = [\operatorname{T} ] ^{\gamma}_{\beta}+[\operatorname{U} ]^{\gamma}_{\beta} 임을 알 수 있다. ■

Composition of Linear Map✔

정리 2.9

F\mathbf{F}-벡터공간 V,W,Z\mathbf{V} ,\mathbf{W} , \mathbf{Z} 와 선형변환 T⁡:V→W,U⁡:W→Z\operatorname{T} : \mathbf{V} \to \mathbf{W} , \operatorname{U} : \mathbf{W} \to \mathbf{Z} 에 대하여 두 선형변환의 합성 U⁡T⁡:V→Z\operatorname{U} \operatorname{T} : \mathbf{V} \to \mathbf{Z} 는 선형이다.

  • 두 선형변환 U⁡,T⁡\operatorname{U} , \operatorname{T} 의 합성 U⁡∘T⁡\operatorname{U} \circ \operatorname{T} 을 편의상 U⁡T⁡\operatorname{U} \operatorname{T} 로 표기하자.

  • 증명

    x,y∈V,a∈Fx, y \in \mathbf{V} , a \in \mathbf{F} 에 대하여

    U⁡T⁡(ax+y)=U⁡(T⁡(ax+y))=U⁡(aT⁡(x)+T⁡(y))=aU⁡(T⁡(x))+U⁡(T⁡(y))=a(U⁡T⁡)(x)+U⁡T⁡(y) \begin{align}\begin{split} \operatorname{U} \operatorname{T} (ax + y)&= \operatorname{U} (\operatorname{T} (ax +y)) \\ &= \operatorname{U} (a \operatorname{T} (x) + \operatorname{T} (y))\\ &=a \operatorname{U} (\operatorname{T} (x)) + \operatorname{U} (\operatorname{T} (y)) \\ &=a (\operatorname{U} \operatorname{T} )(x) + \operatorname{U} \operatorname{T} (y) \\ \end{split}\end{align}\tag*{}

    이 성립한다. ■

문제 2.3-12

F\mathbf{F}-벡터공간 V,W,Z\mathbf{V} ,\mathbf{W} , \mathbf{Z} 와 선형변환 T⁡:V→W,U⁡:W→Z\operatorname{T} : \mathbf{V} \to \mathbf{W} , \operatorname{U} : \mathbf{W} \to \mathbf{Z} 과 그 합성변환 U⁡T⁡:V→Z\operatorname{U}\operatorname{T} : \mathbf{V} \to \mathbf{Z} 대하여 다음이 성립한다.

  1. U⁡T⁡\operatorname{U}\operatorname{T} 가 단사이면 T⁡\operatorname{T} 도 단사이다.

  2. U⁡T⁡\operatorname{U}\operatorname{T} 가 전사이면 U⁡\operatorname{U} 도 전사이다.

  3. T⁡,U⁡\operatorname{T} , \operatorname{U} 가 전단사이면 U⁡T⁡\operatorname{U}\operatorname{T} 도 전단사이다.

  • 증명

    1:

    U⁡∘T⁡\operatorname{U} \circ \operatorname{T} 가 단사이면 S∘(U⁡∘T⁡)=I⁡V\mathbf{S} \circ (\operatorname{U} \circ \operatorname{T} ) = \operatorname{I} _{\mathbf{V}} 을 만족하는 변환 S:Z→V\mathbf{S}: \mathbf{Z} \to \mathbf{V} 가 존재한다. 함수의 합성은 결합법칙을 만족하므로

    S∘(U⁡∘T⁡)=(S∘U⁡)∘T⁡=I⁡V \mathbf{S} \circ (\operatorname{U} \circ \operatorname{T} ) = (\mathbf{S} \circ \operatorname{U} ) \circ \operatorname{T} = \operatorname{I} _{\mathbf{V} }

    이다. 단사함수와의 동치명제에 대한 정리에 의하여 T⁡\operatorname{T} 는 단사이다. ▲

    이로써 U⁡T⁡,T⁡\operatorname{U}\operatorname{T}, \operatorname{T} 가 단사임을 가정할 수 있다. 이제 U⁡T⁡\operatorname{U}\operatorname{T} 가 단사이면 U⁡\operatorname{U} 도 단사여야 하는지 살펴보자. U⁡\operatorname{U} 가 단사가 아니라고 가정하면 U⁡(y1)=U⁡(y2)⟹y1≠y2\operatorname{U} (y_1) = \operatorname{U} (y_2) \implies y_1 \neq y_2 를 만족하는 y1,y2∈Wy_1, y_2 \in \mathbf{W} 가 존재한다. y1=T⁡(x1),y2=T⁡(x2)y_1 = \operatorname{T} (x_1), y_2 = \operatorname{T} (x_2) 라고 하면

    U⁡(T⁡(x1))=U⁡(T⁡(x2)) \operatorname{U} (\operatorname{T} (x_1)) = \operatorname{U} (\operatorname{T} (x_2))

    이므로 U⁡T⁡\operatorname{U}\operatorname{T} 가 단사인 것에서 x1=x2x_1 = x_2 이다. 그러면 T⁡(x1)=T⁡(x2)=y1=y2\operatorname{T} (x_1) = \operatorname{T} (x_2) = y_1 = y_2 이다. 이는 모순이다. 그러므로 U⁡\operatorname{U} 는 단사이다.

    그러나 y1=T⁡(x1),y2=T⁡(x2)y_1 = \operatorname{T} (x_1), y_2 = \operatorname{T} (x_2) 를 가정할 수 없는 경우 즉, T⁡\operatorname{T} 의 함수값이 y1,y2y_1, y_2 에서 정의되지 않은 경우 U⁡\operatorname{U} 가 단사라는 것을 보장 할 수 없다. 실제로 U⁡\operatorname{U} 가 W→Z\mathbf{W} \to \mathbf{Z} 위에서 단사가 아니어도 T⁡\operatorname{T} 의 함수값이 정의된 곳에서, 즉 im⁡(T⁡)→Z\operatorname{im} (\operatorname{T}) \to \mathbf{Z} 위에서는 U⁡\operatorname{U} 가 단사라면 U⁡T⁡\operatorname{U}\operatorname{T} 가 단사라는 조건에 모순되지 않는다. 그러므로 U⁡\operatorname{U} 가 반드시 단사라고 할 수 없다. ▲

    2:

    U⁡∘T⁡\operatorname{U} \circ \operatorname{T} 가 전사이면 (U⁡∘T⁡)∘S=I⁡W(\operatorname{U} \circ \operatorname{T} ) \circ \mathbf{S} = \operatorname{I} _{\mathbf{W}} 을 만족하는 변환 S:Z→V\mathbf{S}: \mathbf{Z}\to \mathbf{V} 가 존재한다. 함수의 합성은 결합법칙을 만족하므로

    (U⁡∘T⁡)∘S=U⁡∘(T⁡∘S)=I⁡W (\operatorname{U} \circ \operatorname{T} ) \circ \mathbf{S} = \operatorname{U} \circ (\operatorname{T} \circ \mathbf{S} ) = \operatorname{I} _{\mathbf{W} }

    이다. 전사함수와의 동치명제에 대한 정리에 의하여 T⁡\operatorname{T} 는 단사이다. ▲

    이로써 U⁡T⁡,T⁡\operatorname{U}\operatorname{T}, \operatorname{T} 가 전사임을 가정할 수 있다. T⁡\operatorname{T} 도 전사여야 하는지 살펴보자. T⁡\operatorname{T} 가 전사가 아니라면 x∈W∧x∉im⁡(T⁡)x \in \mathbf{W} \land x \not\in \operatorname{im} (\operatorname{T}) 인 xx 가 존재한다. U⁡\operatorname{U} 가 전사이므로 T⁡\operatorname{T} 의 함수값이 정의되지 않은 x∈Wx \in \mathbf{W} 에 대한 함수값 U⁡(x)∈Z\operatorname{U} (x) \in \mathbf{Z} 가 항상 존재한다. 따라서 U⁡T⁡\operatorname{U}\operatorname{T} 가 전사이기 위하여 U⁡(x)=U⁡(T⁡(a))\operatorname{U} (x) = \operatorname{U} (\operatorname{T} (a)) 를 만족하는 a∈Va \in \mathbf{V} 가 존재해야 한다. 즉, 조건

    x∈W∧x∉im⁡(T⁡)⟹a∈im⁡(T⁡)∧U⁡(T⁡(a))=U⁡(x) x \in \mathbf{W} \land x \not\in \operatorname{im} (\operatorname{T}) \implies a \in \operatorname{im} (\operatorname{T}) \land \operatorname{U} (\operatorname{T} (a)) = \operatorname{U} (x)

    이 만족된다면 T⁡\operatorname{T} 가 전사일 필요는 없다. ▲

    3:

    T⁡,U⁡\operatorname{T} , \operatorname{U} 가 전단사이면 역함수 T⁡−1:W→V,U⁡−1:Z→W\operatorname{T}^{-1} : \mathbf{W} \to \mathbf{V} , \operatorname{U} ^{-1} : \mathbf{Z}\to \mathbf{W} 가 존재한다. 또한 함수의 합성은 결합법칙을 만족하므로

    (U⁡∘T⁡)∘(T⁡−1∘U⁡−1)=U⁡∘I⁡W∘U⁡−1=I⁡Z (\operatorname{U} \circ \operatorname{T}) \circ (\operatorname{T} ^{-1} \circ \operatorname{U} ^{-1}) = \operatorname{U} \circ \operatorname{I} _{\mathbf{W}} \circ \operatorname{U} ^{-1} = \operatorname{I} _{\mathbf{Z}}
    (T⁡−1∘U⁡−1)∘(U⁡∘T⁡)=T⁡−1∘I⁡W∘T⁡=I⁡V (\operatorname{T} ^{-1} \circ \operatorname{U} ^{-1}) \circ (\operatorname{U} \circ \operatorname{T}) = \operatorname{T} ^{-1} \circ \operatorname{I} _{\mathbf{W}} \circ \operatorname{T} = \operatorname{I} _{\mathbf{V} }

    이다. 역함수가 존재함은 전단사 함수인 것과 동치 이므로 U⁡T⁡\operatorname{U} \operatorname{T} 는 전단사이다. ■

정리 2.10

체 F\mathbf{F} 에 대한 F\mathbf{F}-벡터공간 V\mathbf{V} 와 선형연산자 T⁡,U⁡1,U⁡2\operatorname{T} , \operatorname{U} _1, \operatorname{U} _2 에 대하여 다음이 성립한다.

  1. T⁡(U⁡1+U⁡2)=T⁡U⁡1+T⁡U⁡2\operatorname{T} (\operatorname{U} _1 + \operatorname{U} _2) = \operatorname{T} \operatorname{U} _1 + \operatorname{T} \operatorname{U} _2

  2. (U⁡1+U⁡2)T⁡=U⁡1T⁡+U⁡2T⁡(\operatorname{U} _1 + \operatorname{U} _2)\operatorname{T} = \operatorname{U} _1 \operatorname{T} +\operatorname{U} _2 \operatorname{T}

  3. T⁡(U⁡1U⁡2)=(T⁡U⁡1)U⁡2\operatorname{T} (\operatorname{U} _1 \operatorname{U} _2) = (\operatorname{T} \operatorname{U} _1) \operatorname{U} _2

  4. T⁡I⁡=I⁡T⁡=T⁡\operatorname{T} \operatorname{I} = \operatorname{I} \operatorname{T} = \operatorname{T}

  5. ∀a∈F:a(U⁡1U⁡2)=(aU⁡1)U⁡2=U⁡1(aU⁡2)\forall a \in \mathbf{F} : a(\operatorname{U} _1 \operatorname{U} _2) = (a \operatorname{U} _1)\operatorname{U} _2 = \operatorname{U} _1(a \operatorname{U} _2)

  • 1), 2) 는 선형변환이 분배법칙을 만족한다는 것을, 3) 은 선형변환이 결합법칙을 만족한다는 것을 말해준다.

  • 증명

    1:

    함수의 덧셈의 정의에 의하여 다음이 성립한다.

    T⁡(U⁡1+U⁡2)(x)=T⁡(U⁡1(x)+U⁡2(x)) \operatorname{T}(\operatorname{U}_{1} + \operatorname{U}_{2})(x) = \operatorname{T}(\operatorname{U}_{1}(x) + \operatorname{U}_{2}(x))

    이 결과는 선형변환의 정의에 의하여 다음과 같아진다.

    =T⁡(U⁡1(x)+U⁡2(x))=T⁡(U⁡1(x))+T⁡(U⁡2(x))=(T⁡U⁡1)(x)+(T⁡U⁡2)(x) = \operatorname{T}(\operatorname{U}_{1}(x) + \operatorname{U}_{2}(x)) = \operatorname{T}(\operatorname{U}_{1}(x)) + \operatorname{T}(\operatorname{U}_{2}(x)) = (\operatorname{T}\operatorname{U}_{1})(x) + (\operatorname{T}\operatorname{U}_{2})(x)

    이 결과는 다시 함수의 덧셈의 정의에 의하여 다음과 같아진다.

    =(T⁡U⁡1+T⁡U⁡2)(x) = (\operatorname{T}\operatorname{U}_{1} + \operatorname{T}\operatorname{U}_{2})(x)

    따라서 T⁡(U⁡1+U⁡2)=T⁡U⁡1+T⁡U⁡2\operatorname{T} (\operatorname{U} _1 + \operatorname{U} _2) = \operatorname{T} \operatorname{U} _1 + \operatorname{T} \operatorname{U} _2 이다. ▲

    2:

    함수의 덧셈의 정의에 의하여 다음이 성립한다.

    (U⁡1+U⁡2)(T⁡(x))=U⁡1(T⁡(x))+U⁡2(T⁡(x))=(U⁡1T⁡)(x)+(U⁡2T⁡)(x)=(U⁡1T⁡+U⁡2T⁡)(x) \begin{align}\begin{split} (\operatorname{U}_{1} + \operatorname{U}_{2})(\operatorname{T}(x)) & = \operatorname{U}_{1}(\operatorname{T}(x)) + \operatorname{U}_{2}(\operatorname{T}(x)) \\ &=(\operatorname{U}_{1}\operatorname{T})(x) + (\operatorname{U}_{2}\operatorname{T})(x) \\ &= (\operatorname{U}_{1}\operatorname{T} + \operatorname{U}_{2}\operatorname{T})(x) \\ \end{split}\end{align} \tag*{}

    3:

    함수의 합성은 결합법칙을 만족한다. 선형변환은 함수이다. ▲

    4:

    자명하다. ▲

    5:

    함수의 스칼라곱의 정의에 의하여 다음이 성립한다.

    ((aU⁡1)U⁡2)(x)=a(U⁡1U⁡2)(x) ((a \operatorname{U}_{1})\operatorname{U}_{2})(x) = a (\operatorname{U}_{1}\operatorname{U}_{2})(x)

    다시 함수의 스칼라곱의 정의에 의하여 다음이 성립한다.

    (U⁡1(aU⁡2))(x)=U⁡1(a⋅U⁡2(x)) (\operatorname{U}_{1}(a \operatorname{U}_{2}))(x) = \operatorname{U}_{1}(a \cdot \operatorname{U}_{2}(x))

    그러면 다음과 같이 선형변환의 정의에 의하여 스칼라 aa 를 바깥으로 뺄 수 있다.

    U⁡1(a⋅U⁡2(x))=a(U⁡1(U⁡2(x)))=a(U⁡1U⁡2)(x)■ \operatorname{U}_{1}(a \cdot \operatorname{U}_{2}(x)) = a (\operatorname{U}_{1}(\operatorname{U}_{2}(x))) = a (\operatorname{U}_{1}\operatorname{U}_{2})(x) \tag*{■}

  • 이 정리는 선형변환의 정의역과 공역이 같은 경우를 말하고 있지만, 선형변환의 정의역과 공역이 같지 않으면 더 일반적인 결과가 성립한다.

벡터공간 V\mathbf{V} 에서 정의된 선형변환 T⁡∈L(V)\operatorname{T} \in \mathcal{L}(\mathbf{V} ) 와 k∈Nk \in \N 에 대하여 다음과 같이 정의한다.

T⁡k={T⁡k−1T⁡k≥2T⁡k=1I⁡Vk=0 \operatorname{T} ^{k} = \begin{cases} \operatorname{T} ^{k-1} \operatorname{T} & k \geq 2\\ \operatorname{T} & k = 1\\ \operatorname{I} _{\mathbf{V} } & k = 0\\ \end{cases}

  • 예시

    무한번 미분가능한 실함수 집합 V\mathbf{V} 에 대하여 T⁡:V→V,T⁡(f)=f′\operatorname{T} : \mathbf{V} \to \mathbf{V}, \operatorname{T} (f) = f' 와 같이 정의된 선형변환의 합성을 표현할 때

    T⁡T⁡(f)=T⁡2(f)=T⁡(f′)=(f′)′=f′′ \operatorname{T} \operatorname{T} (f) = \operatorname{T} ^{2} (f) = \operatorname{T} (f') = (f')' = f''
    T⁡T⁡T⁡(f)=T⁡3(f)=T⁡2(f′)=T⁡(f′′)=f′′′ \operatorname{T} \operatorname{T} \operatorname{T} (f) = \operatorname{T} ^{3} (f) = \operatorname{T} ^{2} (f') = \operatorname{T} (f'') = f'''

    와 같이 표현한다.

Matrix Multiplication✔

행렬곱(matrix multiplication, matrix product)

m×nm \times n 행렬 AA 와 n×pn \times p 행렬 BB 에 대하여 두 행렬 A,BA, B 의 곱 ABAB 는 1≤i≤m,1≤j≤p1 \leq i \leq m, 1 \leq j \leq p 에 대하여 다음과 같이 정의된 m×pm \times p 행렬이다.

(AB)ij=∑k=1nAikBkj (AB) _{ij} = \sum_{k=1}^{n}A _{ik}B _{kj}

  • 예시(애니메이션)

  • (AB)ij(AB) _{ij} 를 AA 의 ii 행과 BB 의 jj 열의 성분들을 곱하고 합한 것으로 보면 편하다.

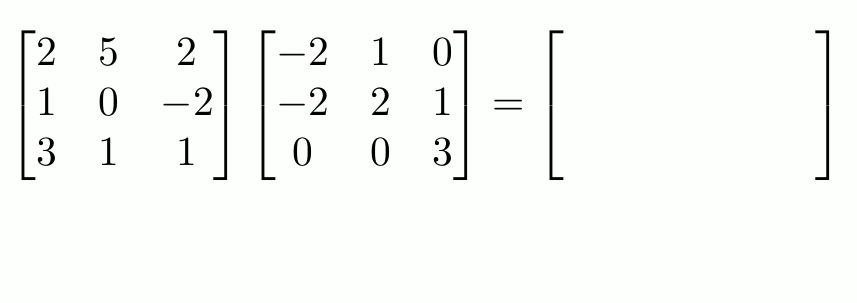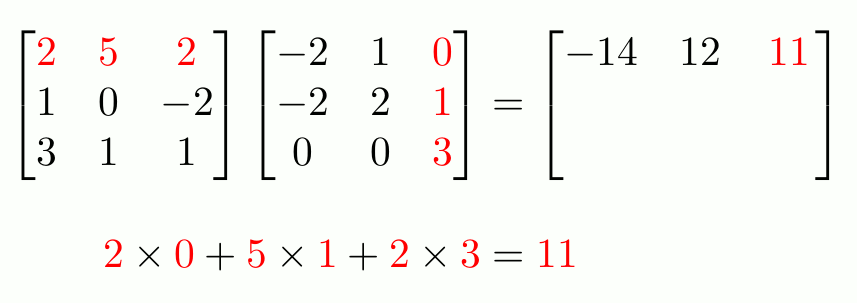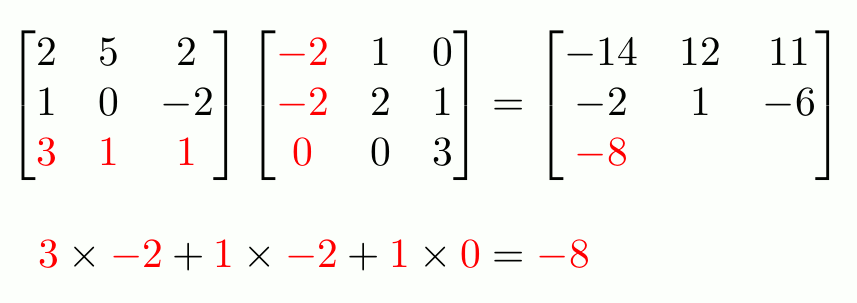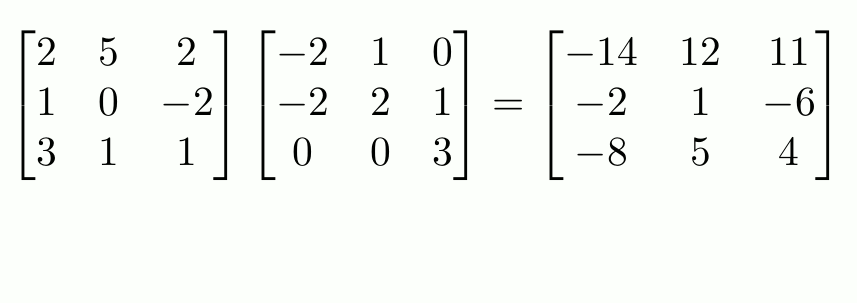
  • 행렬곱이 실제로 어떻게 이루어지는지 살펴보자. m×nm \times n 행렬 AA, n×pn \times p 행렬 BB 의 실제모습을 다음과 같이 살펴보자.

    A=(a11a12…a1na21a22…a2n⋮⋮⋱⋮am1am2…amn),B=(b11b12…b1pb21b22…b2p⋮⋮⋱⋮bn1bn2…bnp) A = \begin{pmatrix} a _{11} & a _{12} & \dots & a _{1n}\\ a _{21} & a _{22} & \dots & a _{2n}\\ \vdots& \vdots& \ddots& \vdots \\ a _{m1} & a _{m2} & \dots & a _{mn}\\ \end{pmatrix}, B = \begin{pmatrix} b_{11} & b_{12} & \dots & b_{1p}\\ b_{21} & b_{22} & \dots & b_{2p}\\ \vdots& \vdots& \ddots& \vdots \\ b_{n1} & b_{n2} & \dots & b_{np}\\ \end{pmatrix}

    이 두 행렬의 행렬곱 m×pm \times p 행렬 ABAB 의 실제 모습은 다음과 같다.

    AB=(a11b11+⋯+a1nbn1a11b12+⋯+a1nbn2…a11b1p+⋯+a1nbnpa21b21+⋯+a2nbn1a21b12+⋯+a2nbn2…a21b1p+⋯+a2nbnp⋮⋮⋱⋮am1b11+⋯+amnbn1am1b12+⋯+amnbn2…am1b1p+⋯+amnbnp)=(∑k=1na1kbk1∑k=1na1kbk2…∑k=1na1kbkp∑k=1na2kbk1∑k=1na2kbk2…∑k=1na2kbkp⋮⋮⋱⋮∑k=1namkbk1∑k=1namkbk2…∑k=1namkbkp) \begin{align}\begin{split} &AB = \\ &\begin{pmatrix} a _{11} b _{11} + \dots + a _{1n} b _{n1} & a _{11} b _{12} + \dots + a _{1n} b _{n2} & \dots& a _{11} b _{1p} + \dots + a _{1n} b _{np} \\ a _{21} b _{21} + \dots + a _{2n} b _{n1} & a _{21} b _{12} + \dots + a _{2n} b _{n2} & \dots& a _{21} b _{1p} + \dots + a _{2n} b _{np} \\ \vdots& \vdots& \ddots& \vdots \\ a _{m1} b _{11} + \dots + a _{mn} b _{n1} & a _{m1} b _{12} + \dots + a _{mn} b _{n2} & \dots& a _{m1} b _{1p} + \dots + a _{mn} b _{np} \\ \end{pmatrix}\\ &= \begin{pmatrix} \sum_{k=1}^{n} a _{1k}b _{k1} & \sum_{k=1}^{n} a _{1k}b _{k2} & \dots& \sum_{k=1}^{n} a _{1k}b _{kp} \\ \sum_{k=1}^{n} a _{2k}b _{k1} & \sum_{k=1}^{n} a _{2k}b _{k2} & \dots& \sum_{k=1}^{n} a _{2k}b _{kp} \\ \vdots& \vdots& \ddots& \vdots \\ \sum_{k=1}^{n} a _{mk}b _{k1} & \sum_{k=1}^{n} a _{mk}b _{k2} & \dots& \sum_{k=1}^{n} a _{mk}b _{kp} \\ \end{pmatrix} \end{split}\end{align} \tag*{}

    그러므로 m×pm \times p 행렬 ABAB 의 ii 열 jj 행 성분은 다음과 같다.

    (AB)ij=∑k=1naikbkj (AB) _{ij} = \sum_{k=1}^{n} a _{ik}b _{kj}

  • 지금까지 하고 있는 일은 선형변환과 행렬 간의 대응관계를 연구하는 것이다. 먼저 선형변환과 행렬의 대응을 살펴보았다. 그리고 선형변환의 합과 스칼라곱을 정의한 다음 이 연산이 행렬에서의 합과 스칼라곱의 구조를 보존한다는 것을 증명했다. 이제 두 선형변환의 합성에 어떤 행렬의 연산이 대응되는지 연구해야 한다. 즉, 행렬곱에 대하여 정의할 차례인 것이다.

    그렇다면 행렬 곱은 어째서 이렇게 정의되었나? 행렬 곱 정의가 두 선형변환의 합성의 구조를 보존해야 하기 때문이다.

    유한차원 벡터공간 V,W,Z\mathbf{V} ,\mathbf{W} ,\mathbf{Z} 와 선형변환 T⁡:V→W,U⁡:W→Z\operatorname{T} : \mathbf{V} \to \mathbf{W} , \operatorname{U} : \mathbf{W} \to \mathbf{Z} 를 생각하자. 이때 V,W,Z\mathbf{V}, \mathbf{W}, \mathbf{Z} 의 순서기저를 각각

    α={v1,…,vn} \alpha = \{v_1, \dots, v_n\}
    β={w1,…,wm} \beta = \{w_1, \dots, w_m\}
    γ={z1,…,zp} \gamma = \{z_1, \dots, z_p\}

    으로 정의하고 선형변환 T⁡,U⁡\operatorname{T} , \operatorname{U} 의 행렬표현을

    B=[T⁡]αβ∈Fm×n B = [\operatorname{T} ] ^{\beta }_{\alpha } \in \mathbf{F}^{m \times n}
    A=[U⁡]βγ∈Fp×m A = [\operatorname{U} ] ^{\gamma}_{\beta} \in \mathbf{F}^{p \times m}

    라고 하자. 그러면 U⁡T⁡:V→Z\operatorname{U} \operatorname{T} : \mathbf{V} \to \mathbf{Z} 에 대하여

    AB=[U⁡T⁡]αγ∈Fp×n \boxed{ AB = [\operatorname{U} \operatorname{T} ] ^{\gamma}_{\alpha } \in \mathbf{F} ^{p \times n}}

    가 성립하도록 행렬곱 ABAB 를 정의하면 된다. j=1,2,…,nj = 1, 2, \dots, n 에 대하여 다음이 성립한다.

    (U⁡T⁡)(vj)=U⁡(T⁡(vj))=U⁡(∑k=1mBkjwk)=∑k=1mBkjU⁡(wk)=∑k=1mBkj(∑i=1pAikzi)=∑i=1p(∑k=1mAikBkj)zi \begin{align}\begin{split} (\operatorname{U} \operatorname{T} ) (v_j) &= \operatorname{U} (\operatorname{T} (v_j)) = \operatorname{U} \bigg (\sum_{k=1}^{m}B _{kj} w_k\bigg ) = \sum_{k=1}^{m}B _{kj}\operatorname{U} (w_k) \\ &= \sum_{k=1}^{m}B _{kj} \bigg (\sum_{i=1}^{p}A _{ik}z_i\bigg ) = \sum_{i=1}^{p} \bigg (\sum_{k=1}^{m}A _{ik}B _{kj}\bigg ) z_i \\ \end{split}\end{align}\tag*{}

    그러므로 행렬곱 ABAB 를 다음과 같은 p×np \times n 행렬로 정의할 수 있다.

    (AB)ij=∑k=1mAikBkj \boxed{ (AB) _{ij} = \sum_{k=1}^{m}A _{ik} B _{kj} }

  • 행렬 A,BA, B 의 형상이 다음과 같이 맞아야 행렬곱 연산을 할 수 있다.

    (m×n)(n×p)=(m×p) (m \times n) (n \times p) = (m \times p)

    내부 차원이 맞아야 행렬 곱 ABAB 가 정의되고, 외부 차원이 행렬 ABAB 의 크기를 결정한다.

  • 예시

    다음과 같이 (2×3)(3×1)=2×1(2 \times 3) (3 \times 1) = 2 \times 1 이다.

    (12104−1)(425)=(133) \begin{pmatrix} 1&2&1\\ 0&4&-1\\ \end{pmatrix} \begin{pmatrix} 4\\ 2\\ 5\\ \end{pmatrix} = \begin{pmatrix} 13\\ 3\\ \end{pmatrix}

  • 함수의 합성에 교환법칙이 성립하지 않으므로 행렬곱에도 교환법칙이 성립하지 않는다.

  • 예시

    다음은 두 행렬 A,BA,B 가 AB≠BAAB \neq BA 을 만족한다.

    (1100)(0110)=(1100),(0110)(1100)=(0011) \begin{pmatrix} 1&1\\ 0&0\\ \end{pmatrix} \begin{pmatrix} 0 & 1\\ 1 & 0\\ \end{pmatrix} = \begin{pmatrix} 1 & 1\\ 0 & 0\\ \end{pmatrix} , \quad \begin{pmatrix} 0&1\\ 1&0\\ \end{pmatrix} \begin{pmatrix} 1&1\\ 0&0\\ \end{pmatrix} = \begin{pmatrix} 0&0\\ 1&1\\ \end{pmatrix}

m×nm \times n 행렬과 항등행렬 Im,InI_m, I_n 에 대하여 다음이 성립한다.

ImA=AIn=A I_mA = AI_n = A
  • 증명
(AB)⊤=B⊤A⊤ (AB) ^{\top} = B ^{\top} A ^{\top}

  • 증명

    (AB)ij⊤=(AB)ji=∑k=1nAjkBki(AB) ^{\top} _{ij} = (AB) _{ji} = \sum_{k=1}^{n}A _{jk}B _{ki}
    (B⊤A⊤)ij=∑k=1n(B⊤)ik(A⊤)kj=∑k=1nBkiAjk(B ^{\top} A ^{\top}) _{ij} = \sum_{k=1}^{n}(B ^{\top})_{ik}(A ^{\top}) _{kj} = \sum_{k=1}^{n}B _{ki}A _{jk}

정리 2.11

유한차원 벡터공간 V,W,Z\mathbf{V} , \mathbf{W} , \mathbf{Z} 와 각각의 순서기저 α,β,γ\alpha , \beta , \gamma 와 선형변환 T⁡:V→W,U⁡:W→Z\operatorname{T} : \mathbf{V} \to \mathbf{W} , \operatorname{U} : \mathbf{W} \to \mathbf{Z} 에 대하여 다음이 성립한다.

[U⁡T⁡]αγ=[U⁡]βγ[T⁡]αβ [\operatorname{U} \operatorname{T} ] ^{\gamma}_{\alpha } = [\operatorname{U} ] ^{\gamma}_{\beta} [\operatorname{T} ] ^{\beta }_{\alpha }
  • 이 정리가 행렬 곱 연산이 두 선형변환의 합성의 구조를 보존한다는 것을 말해준다.

  • 증명

    행렬곱의 정의에 의하여 이 정리가 성립함을 쉽게 알 수 있다.

  • 예시

    선형변환 U⁡:P3(R),T⁡:P2(R)→P3(R)\operatorname{U}: \mathbf{P} _3(\R), \operatorname{T}:\mathbf{P} _2(\R) \to \mathbf{P} _3(\R) 를

    U⁡(f(x))=f′(x),T⁡(f(x))=∫0xf(t)dt \operatorname{U} (f(x)) = f'(x), \quad \operatorname{T} (f(x)) = \int_{0}^{x}f(t)dt

    로 정의하면 U⁡T⁡=I⁡\operatorname{U} \operatorname{T} = \operatorname{I} 이다. α,β\alpha , \beta 를 P3(R),P2(R)\mathbf{P} _3(\R), \mathbf{P} _2(\R) 의 표준순서기저라 하면 다음이 성립한다.

    [U⁡T⁡]β=[U⁡]αβ[T⁡]βα=(010000200003)(00010001200013)=(100010001)=[I⁡]β [\operatorname{U} \operatorname{T} ] _{\beta } = [\operatorname{U} ] ^{\beta }_{\alpha }[\operatorname{T} ]^{\alpha } _{\beta } = \begin{pmatrix} 0&1&0&0\\ 0&0&2&0\\ 0&0&0&3\\ \end{pmatrix}\begin{pmatrix} 0&0&0\\ 1&0&0\\ 0&\dfrac{1}{2}&0\\ 0&0&\dfrac{1}{3}\\ \end{pmatrix} = \begin{pmatrix} 1&0&0\\ 0&1&0\\ 0&0&1\\ \end{pmatrix} = [\operatorname{I} ] _{\beta }

정리 2.11 따름정리

유한차원 벡터공간 V\mathbf{V} 와 순서기저 β\beta 와 선형연산자 T⁡,U⁡∈L(V)\operatorname{T} , \operatorname{U} \in \mathcal{L}(\mathbf{V} ) 에 대하여 다음이 성립한다.

[U⁡T⁡]β=[U⁡]β[T⁡]β [\operatorname{U} \operatorname{T} ] _{\beta } = [\operatorname{U} ] _{\beta }[\operatorname{T} ] _{\beta }

정리 2.12

AA 가 m×nm \times n 행렬, BB 와 CC 가 n×pn \times p 행렬, DD 와 EE 가 q×mq \times m 행렬일 때, 다음이 성립한다.

  1. A(B+C)=AB+AC,(D+E)A=DA+EAA(B+C) = AB+AC, (D+E)A = DA+EA

  2. 임의의 스칼라 aa 에 대하여 a(AB)=(aA)B=A(aB)a(AB) = (aA)B=A(aB)

  3. ImA=A=AInI_mA = A=AI_n

  • 1) 의 증명

    [A(B+C)]ij=∑k=1nAik(B+C)kj=∑k=1nAik(Bkj+Ckj)=∑k=1n(AikBkj+AikCkj)=∑k=1nAikBkj+∑k=1nAikCkj=(AB)ij+(AC)ij=[AB+AC]ij \begin{align}\begin{split} [A(B+C)] _{ij} &= \sum_{k=1}^{n}A _{ik}(B+C) _{kj} = \sum_{k=1}^{n}A _{ik}(B _{kj} + C _{kj}) \\ &= \sum_{k=1}^{n} (A _{ik}B _{kj} + A _{ik}C _{kj}) = \sum_{k=1}^{n} A _{ik} B _{kj} + \sum_{k=1}^{n} A _{ik} C _{kj} \\ &= (AB) _{ij} + (AC) _{ij} = [AB +AC] _{ij} \end{split}\end{align}\tag*{}
    ⟺A(B+C)=AB+AC \iff A(B+C) = AB+AC

  • 3) 의 증명

    (ImA)ij=∑k=1m(Im)ikAkj=∑k=1mδikAkj=Aij\displaystyle (I_mA) _{ij} = \sum_{k=1}^{m}(I_m) _{ik}A _{kj} = \sum_{k=1}^{m}\delta _{ik}A _{kj} = A _{ij}

정리 2.12 따름정리

m×nm \times n 행렬 AA 와 n×pn \times p 행렬 B1,B2,…,BkB_1, B_2, \dots, B_k 와 q×mq \times m 행렬 C1,C2,…,CkC_1, C_2, \dots, C_k 와 스칼라 a1,a2,…,aka_1, a_2, \dots, a_k 에 대하여 다음이 성립한다.

A(∑i=1kaiBi)=∑i=1kaiABi,(∑i=1kaiCi)A=∑i=1kaiCiA A \bigg (\sum_{i=1}^{k}a_iB_i\bigg ) = \sum_{i=1}^{k}a_iAB_i, \quad \bigg (\sum_{i=1}^{k}a_iC_i\bigg )A = \sum_{i=1}^{k}a_iC_iA
  • 증명

n×nn \times n 행렬 AA 에 대하여 행렬의 지수를 다음과 같이 정의한다.

Ak={Ak−1Ak≥2Ak=1Ink=0 A ^{k} = \begin{cases} A ^{k-1}A & k \geq 2\\ A & k = 1\\ I_n & k = 0\\ \end{cases}

행렬곱에서 소거법칙이 성립하지 않는다.

  • 증명

    A=(0010)⟹A≠O∧A2=OA = \begin{pmatrix} 0&0\\ 1&0\\ \end{pmatrix} \implies A \neq O \land A ^{2} = O 이다. 이때 소거법칙이 성립한다고 가정하면

    A⋅A=A2=O=A⋅O⟹A=O A \cdot A = A ^{2} = O = A \cdot O \implies A = O

    이다. 이는 모순이다. ■

정리 2.13

m×nm \times n 행렬 AA 와 n×pn \times p 행렬 BB 와 j=1,2,…,pj = 1, 2, \dots, p 에 대하여 ABAB 의 jj 열을 uju_j, BB 의 jj 열을 vjv_j 이라 하면 다음이 성립한다.

  1. uj=Avju_j = Av_j

  2. vj=Bejv_j = Be_j (단, eje_j 는 Fp\mathbf{F} ^{p} 의 jj 번째 표준벡터)

  • 증명

    1:

    uj=((AB)1j(AB)2j⋮(AB)mj)=(∑k=1nA1kBkj∑k=1nA2kBkj⋮∑k=1nAmkBkj)=A(B1jB2j⋮Bnj)=Avj■ u_j = \begin{pmatrix} (AB) _{1j}\\ (AB) _{2j}\\ \vdots \\ (AB) _{mj}\\ \end{pmatrix} = \begin{pmatrix} \sum_{k=1}^{n}A _{1k}B _{kj}\\ \sum_{k=1}^{n}A _{2k}B _{kj}\\ \vdots\\ \sum_{k=1}^{n}A _{mk}B _{kj}\\ \end{pmatrix} = A \begin{pmatrix} B _{1j}\\ B _{2j}\\ \vdots \\ B _{nj}\\ \end{pmatrix} = A v_j \tag*{■}

    2:

    Bej=(b11b12…b1pb21b22…b2p⋮⋮⋱⋮bn1bn2…bnp)(00⋮1⋮0)=(b1jb2j…bnj)■ Be_j = \begin{pmatrix} b_{11} & b_{12} & \dots & b_{1p}\\ b_{21} & b_{22} & \dots & b_{2p}\\ \vdots& \vdots& \ddots& \vdots \\ b_{n1} & b_{n2} & \dots & b_{np}\\ \end{pmatrix} \begin{pmatrix} 0\\ 0\\ \vdots \\ 1\\ \vdots \\ 0\\ \end{pmatrix} = \begin{pmatrix} b_{1j}\\ b_{2j}\\ \dots\\ b_{nj}\\ \end{pmatrix} \tag*{■}

정리 2.14

유한차원 벡터공간 V,W\mathbf{V} , \mathbf{W} 과 각각의 순서기저 β,γ\beta , \gamma 에 대한 선형변환 T⁡:V→W\operatorname{T} : \mathbf{V} \to \mathbf{W} 과 u∈Vu \in \mathbf{V} 에 대하여 다음이 성립한다.

[T⁡(u)]γ=[T⁡]βγ[u]β [\operatorname{T} (u)] _{\gamma } = [\operatorname{T} ] ^{\gamma}_{\beta} [u] _{\beta }

  • 이 정리는 선형변환에 어떤 벡터를 입력하여 행렬로 표현한 것과 선형변환과 벡터를 행렬로 표현한 후 행렬곱 한 것이 같음을 말해준다.

  • 증명

    u∈Vu \in \mathbf{V} 를 고정하고 다음과 같은 선형변환 f:F→V,g:F→Wf: F \to \mathbf{V} , g: F \to \mathbf{W} 를 정의하자.

    ∀a∈F:f(a)=au,g(a)=aT⁡(u) \forall a \in F : f(a) = au, g(a) = a \operatorname{T} (u)

    FF 의 표준순서기저를 α={1}\alpha = \{1\} 라고 하자. 선형변환의 조건 에 의하여 g(a)=aT⁡(u)=T⁡(au)=T⁡f(a)g(a) = a \operatorname{T} (u) = \operatorname{T} (au) = \operatorname{T} f(a) 이므로 g=T⁡fg = \operatorname{T} f 이다.

    행렬의 각 열을 벡터로 보고 정리 2.11 을 적용하면 다음이 성립한다.

    [T⁡(u)]γ=[g(1)]γ=[g]αγ=[T⁡f]αγ=[T⁡]βγ[f]αβ=[T⁡]βγ[f(1)]β=[T⁡]βγ[u]β■ [\operatorname{T} (u)] _{\gamma } = [g(1)] _{\gamma } = [g] ^{\gamma}_{\alpha } = [\operatorname{T} f] ^{\gamma}_{\alpha } = [\operatorname{T} ] ^{\gamma}_{\beta} [f] ^{\beta }_{\alpha } = [\operatorname{T} ] ^{\gamma}_{\beta} [f(1)] _{\beta } = [\operatorname{T} ]^{\gamma}_{\beta} [u] _{\beta } \tag*{■}

Left Multiplication Transformation✔

좌측 곱 변환(left multiplication transformation)

체 F\mathbf{F} 에서 성분을 가져온 m×nm \times n 행렬 AA 에 대하여 다음과 같은 선형변환을 좌측 곱 변환이라 한다.

L⁡A:Fn→Fm,x↦Ax \operatorname{L} _{A} : \mathbf{F} ^{n} \to \mathbf{F} ^{m}, x \mapsto Ax

  • xx 는 Fn\mathbf{F} ^{n} 의 열벡터이다.

  • 좌측 곱 변환은 선형변환의 성질로 행렬의 성질을 유추하거나, 행렬의 성질로 선형변환의 성질을 유추할 때 유용하게 사용되는 도구이다.

  • 예시

    A=(121012),x=(13−1)A = \begin{pmatrix} 1&2&1\\ 0&1&2\\ \end{pmatrix}, x= \begin{pmatrix} 1\\ 3\\ -1\\ \end{pmatrix} 에 대하여 다음이 성립한다.

    L⁡A(x)=Ax=(121012)(13−1)=(61)\operatorname{L} _A(x) = Ax = \begin{pmatrix} 1&2&1\\ 0&1&2\\ \end{pmatrix}\begin{pmatrix} 1\\ 3\\ -1\\ \end{pmatrix} = \begin{pmatrix} 6\\ 1\\ \end{pmatrix}

정리 2.15

체 F\mathbf{F} 에서 성분을 가져온 m×nm \times n 행렬 AA 에 대하여 좌측 곱 변환 L⁡A:Fn→Fm\operatorname{L} _{A}: \mathbf{F} ^{n} \to \mathbf{F} ^{m} 은 선형이다.

또한 체 F\mathbf{F} 에서 성분을 가져온 m×nm \times n 행렬 BB 와 Fn\mathbf{F} ^{n} 의 표준순서기저 β\beta, Fm\mathbf{F} ^{m} 의 표준순서기저 γ\gamma 에 대하여 다음이 성립한다.

  1. [L⁡A]βγ=A[\operatorname{L} _A] ^{\gamma}_{\beta} = A

  2. L⁡A=L⁡B⟺A=B\operatorname{L} _A = \operatorname{L} _B \iff A = B

  3. L⁡A+B=L⁡A+L⁡B\operatorname{L} _{A+B} = \operatorname{L} _A + \operatorname{L} _B

  4. ∀a∈F:L⁡aA=aL⁡A\forall a \in \mathbf{F} : \operatorname{L} _{aA} = a \operatorname{L} _A

  5. T⁡:Fn→Fm\operatorname{T} : \mathbf{F} ^{n} \to \mathbf{F} ^{m} 이 선형이면 T⁡=L⁡C\operatorname{T} = \operatorname{L} _C 인 m×nm \times n 행렬 CC 가 유일하게 존재한다. 또한 C=[T⁡]βγC = [\operatorname{T} ] ^{\gamma}_{\beta} 이다.

  6. n×pn \times p 행렬 EE 에 대하여 L⁡AE=L⁡AL⁡E\operatorname{L} _{AE} = \operatorname{L} _A \operatorname{L} _E 이다.

  7. m=n⟹L⁡In=I⁡Fnm = n \implies \operatorname{L} _{I_n} = \operatorname{I} _{\mathbf{F} ^{n}}
  • 이 정리는 L⁡A\operatorname{L} _A 가 선형이고 유용한 도구를 많이 제공한다는 것을 말해준다.

  • 증명

    L⁡A\operatorname{L}_{A} 는 선형이다:

    정리 2.12 에 의하여 A(B+C)=AB+ACA(B+C) = AB+AC 이다. 이는 L⁡A(x+y)=A(x+y)=Ax+Ay=L⁡(x)+L⁡(y)\operatorname{L} _A(x + y) = A(x+y) = Ax + Ay = \operatorname{L} (x) + \operatorname{L} (y) 임을 뜻한다.

    또한 정리 2.12 에 의하여 스칼라 aa 에 대하여 A(aB)=a(AB)A(aB) = a(AB) 이다. 이는 L⁡A(cx)=A(cx)=c(Ax)=cL⁡(x)\operatorname{L} _A(cx) = A(cx) = c(Ax) = c\operatorname{L} (x) 임을 뜻한다. 그러므로 L⁡A\operatorname{L} _A 는 선형이다. ▲

    1:

    일단 β={e1,e2,…,en}\beta = \{e_1, e_2, \dots, e_n\} 이고 γ={e1,e2,…,em}\gamma = \{e_1, e_2, \dots, e_m\} 이다.

    [L⁡A]βγ[\operatorname{L}_{A}] ^{\gamma}_{\beta} 의 jj 열은 [L⁡A(ej)]γ=[Aej]γ[\operatorname{L}_{A}(e_j)] _{\gamma} = [Ae_j] _{\gamma} 인데 AejAe_j 는 AA 의 jj 열이다. 또 [Aej]γ[Ae_j] _{\gamma } 는 표준순서기저로 AA 의 jj 열을 나타낸 행렬이므로 결국 다시 AA 의 jj 열이 된다. 이는 [L⁡A]βγ[\operatorname{L}_{A}]^{\gamma}_{\beta} 의 모든 열이 AA 의 열임을 뜻한다. 그러므로 [L⁡A]βγ=A[\operatorname{L}_{A}]^{\gamma}_{\beta} = A 이다. ▲

    2:

    이미 증명한 1) 에 의하여

    A=[L⁡A]βγ=[L⁡B]βγ=B A = [\operatorname{L}_{A}] ^{\gamma}_{\beta} = [\operatorname{L}_{B}] ^{\gamma}_{\beta} = B

    이다. 그 역도 쉽게 증명가능하다. ▲

    3:

    이미 증명한 1) 과 정리 2.8 - 1 에 의하여 다음이 성립한다.

    [L⁡A+B]βγ=A+B=[L⁡A]βγ+[L⁡B]βγ=[L⁡A+L⁡B]βγ▲ [\operatorname{L}_{A+B}] ^{\gamma}_{\beta} = A + B = [\operatorname{L}_{A}] ^{\gamma}_{\beta} + [\operatorname{L}_{B}] ^{\gamma}_{\beta} = [\operatorname{L}_{A} + \operatorname{L}_{B}] ^{\gamma}_{\beta} \tag*{▲}

    4:

    [L⁡aA]βγ=aA=a[L⁡A]βγ▲ [\operatorname{L}_{aA}]^{\gamma}_{\beta} = aA = a[\operatorname{L}_{A}]^{\gamma}_{\beta} \tag*{▲}

    5:

    C=[T⁡]βγC = [\operatorname{T} ] ^{\gamma}_{\beta} 라고 하자. 정리 2.14 에 의하여 [T⁡(x)]βγ=[T⁡]βγ[x]β=C[x]β[\operatorname{T} (x)]^{\gamma}_{\beta} = [\operatorname{T}]^{\gamma}_{\beta} [x]_{\beta } = C[x]_{\beta} 이므로

    ∀x∈Fn:T⁡(x)=Cx=L⁡C(x)\forall x \in \mathbf{F} ^{n} : \operatorname{T} (x) = Cx = \operatorname{L}_{C}(x)

    이다. 이는 T⁡=L⁡C\operatorname{T} = \operatorname{L}_{C} 을 의미한다. 이로써 CC 의 존재성이 증명되었다. CC 의 유일성은 2) 에서 곧바로 알 수 있다. ▲

    6:

    (AE)ej(AE)e_j 는 AEAE 의 jj 열이다. 정리 2.13 - 1 에 의하여 AEAE 의 jj 열은 A(Bej)A(Be_j) 이다. 그러므로

    L⁡AE(ej)=(AE)ej=A(Eej)=L⁡A(Eej)=L⁡A(L⁡E(ej)) \operatorname{L}_{AE}(e_j) = (AE)e_j = A(Ee_j) = \operatorname{L}_{A}(Ee_j) = \operatorname{L}_{A}(\operatorname{L}_{E}(e_j))

    이다. 정리 2.6 따름정리 에 의하여 L⁡AE=L⁡AL⁡E\operatorname{L}_{AE} = \operatorname{L}_{A}\operatorname{L}_{E} 이다. ▲

    7:

    먼저 [L⁡In]βγ=In[\operatorname{L}_{I_n}] ^{\gamma}_{\beta} = I_n 이다.

    [I⁡Fn]β[\operatorname{I} _{\mathbf{F} ^{n}}] _{\beta } 의 jj 열은 [I⁡Fn(ej)]β=[ej]β[\operatorname{I} _{\mathbf{F} ^{n}}(e_j)] _{\beta} = [e_j] _{\beta} 이다. 이는 eje_j 를 뜻한다. 그러므로 [I⁡Fn]β=In[\operatorname{I} _{\mathbf{F} ^{n}}] _{\beta } = I_n 이다. ■

정리 2.16

A(BC)A(BC) 가 정의된 행렬 A,B,CA, B, C 에 대하여 다음이 성립한다.

  1. (AB)C(AB)C 가 정의되어 있다.

  2. A(BC)=(AB)CA(BC) = (AB)C 가 성립한다.
  • 2) 는 행렬곱 연산에서 결합법칙이 성립함을 말해준다.

  • 증명

    2:

    함수의 합성은 결합법칙을 만족한다. 또한 정리 2.15 - 6 에 의하여 다음이 성립한다.

    L⁡A(BC)=L⁡AL⁡BC=L⁡A(L⁡BL⁡C)=(L⁡AL⁡B)L⁡C=L⁡ACL⁡C=L⁡(AB)C \operatorname{L}_{A(BC)} = \operatorname{L}_{A}\operatorname{L}_{BC} = \operatorname{L}_{A}(\operatorname{L}_{B}\operatorname{L}_{C}) = (\operatorname{L}_{A}\operatorname{L}_{B})\operatorname{L}_{C} = \operatorname{L}_{AC}\operatorname{L}_{C} = \operatorname{L}_{(AB)C}

    그러므로 정리 2.15 - 2 에 의하여 다음이 성립한다.

    A(BC)=(AB)C■ A(BC) = (AB)C \tag*{■}

  • 이 정리는 지금까지 했던 것처럼 행렬의 성분을 비교하는 방식으로도 증명 가능하다. 그러나 그렇게 번거로운 방법보다 지금까지 정립해온 정리를 사용하면 위와 같이 세련되게 증명할 수 있다.

정리 2.16 따름정리

행렬곱 연산에서 결합법칙이 성립한다.

  • 증명

    정리 2.16 - 2 에 의하여 본 정리가 성립한다.

Invertibility✔

역함수(inverse)

벡터공간 V,W\mathbf{V} ,\mathbf{W} 와 선형변환 T⁡:V→W\operatorname{T} : \mathbf{V} \to \mathbf{W} 에 대하여 다음을 만족하는 함수 T⁡−1:W→V\operatorname{T}^{-1} : \mathbf{W} \to \mathbf{V} 를 T⁡\operatorname{T} 의 역함수라고 한다.

T⁡T⁡−1=I⁡W,T⁡−1T⁡=I⁡V\operatorname{T} \operatorname{T}^{-1} = \operatorname{I} _{\mathbf{W} }, \operatorname{T}^{-1} \operatorname{T} = \operatorname{I} _{\mathbf{V} }

선형변환의 역함수는 유일하다.

선형변환이 가역이기 위한 필요충분조건은 전단사라는 것이다.

가역인 함수 T⁡,U⁡\operatorname{T} , \operatorname{U} 에 대하여 다음이 성립한다.

  1. (T⁡U⁡)−1=U⁡−1T⁡−1(\operatorname{T} \operatorname{U} ) ^{-1} = \operatorname{U} ^{-1} \operatorname{T} ^{-1}

  2. (T⁡−1)−1=T⁡(\operatorname{T} ^{-1}) ^{-1} = \operatorname{T} 이다. 특히 T⁡−1\operatorname{T} ^{-1} 는 가역이다.

  3. dim⁡(V)=dim⁡(W)\dim (\mathbf{V} ) = \dim (\mathbf{W} ) 인 벡터공간 V,W\mathbf{V} , \mathbf{W} 에 대하여 선형변환 T⁡:V→W\operatorname{T} : \mathbf{V} \to \mathbf{W} 가 가역이기 위한 필요충분조건은 rank⁡(T⁡)=dim⁡(V)\operatorname{rank} (\operatorname{T} ) = \dim (\mathbf{V} ) 이다.

  • 증명

    3:

    정리 2.5 에 의하여 T⁡\operatorname{T} 가 전단사라는 것과 rank⁡(T⁡)=dim⁡(V)\operatorname{rank} (\operatorname{T} ) = \dim (\mathbf{V} ) 은 동치이다. 선형변환이 가역이기 위한 필요충분조건은 전단사라는 것이다. ■

  • 예시

    선형변환 T⁡:P1(R)→R2,a+bx↦(a,a+b)\operatorname{T} : \mathbf{P}_{1}(\R) \to \R ^{2}, a+bx \mapsto (a, a+b) 의 역함수는 다음과 같다.

    T⁡−1:R2→P1(R),(c,d)↦c+(d−c)x \operatorname{T} ^{-1}:\R ^{2} \to \mathbf{P}_{1}(\R), (c, d) \mapsto c + (d-c)x

정리 2.17

선형변환의 역함수는 선형이다.

  • 증명

    벡터공간 V,W\mathbf{V} , \mathbf{W} 와 가역인 선형변환 T⁡:V→W\operatorname{T} : \mathbf{V} \to \mathbf{W} 에 대한 역함수 T⁡−1:W→V\operatorname{T} ^{-1}: \mathbf{W} \to \mathbf{V} 가 선형임을 보이자.

    T⁡\operatorname{T} 가 전단사이므로 y1,y2∈Wy_1, y_2 \in \mathbf{W} 에 대한 T⁡(x1)=y1,T⁡(x2)=y2\operatorname{T} (x_1) = y_1, \operatorname{T} (x_2) = y_2 를 만족하는 벡터 x1,x2∈Vx_1, x_2 \in \mathbf{V} 가 유일하게 존재한다. 그러므로 스칼라 c∈Fc \in \mathbf{F} 에 대하여 다음이 성립한다.

    T⁡−1(cy1+y2)=T⁡−1[cT⁡(x1)+T⁡(x2)]=T⁡−1(T⁡(cx1+x2))=cx1+x2=cT⁡−1(y1)+T⁡−1(y2) \begin{align}\begin{split} \operatorname{T} ^{-1}(cy_1 + y_2) &= \operatorname{T} ^{-1}[c \operatorname{T} (x_1) + \operatorname{T} (x_2)] = \operatorname{T} ^{-1}(\operatorname{T} (cx_1 + x_2))\\ &= cx_1 + x_2 = c \operatorname{T} ^{-1} (y_1) + \operatorname{T} ^{-1}(y_2) \end{split}\end{align} \tag*{}

    ■

정리 2.17 따름정리

선형변환 T⁡:V→W\operatorname{T} : \mathbf{V} \to \mathbf{W} 가 가역이면 다음이 성립한다.

  • V\mathbf{V} 가 유한차원인 것과 W\mathbf{W} 가 유한차원인 것은 동치이다.

  • V,W\mathbf{V} , \mathbf{W} 가 유한차원이면 dim⁡(V)=dim⁡(W)\dim (\mathbf{V} ) = \dim (\mathbf{W} ) 이다.

  • 증명

    V\mathbf{V} 가 유한차원이라고 하고 기저를 β={x1,x2,…,xn}\beta = \{x_1, x_2, \dots, x_n\} 이라고 하자. T⁡\operatorname{T} 가 전단사이므로 공역과 치역이 같다. 그러면 정리 2.2 에 의하여 span⁡(T⁡(β))=im⁡(T⁡)=W\operatorname{span} (\operatorname{T} (\beta )) = \operatorname{im} (\operatorname{T}) = \mathbf{W} 이다. 유한집합이 W\mathbf{W} 를 생성하므로 정리 1.9 에 의하여 W\mathbf{W} 는 유한차원이다. ▲

    역으로 W\mathbf{W} 가 유한차원임을 가정하면 T⁡−1\operatorname{T} ^{-1} 를 사용하여 비슷한 논법으로 V\mathbf{V} 가 유한차원임을 증명할 수 있다. ▲

    이제 V,W\mathbf{V} , \mathbf{W} 가 유한차원이라는 사실을 사용할 수 있다. T⁡\operatorname{T} 가 단사이므로 정리 2.4 에 의하여

    ker⁡(T⁡)={0}⟹nullity⁡(T⁡)=0 \ker (\operatorname{T}) = \{0\} \implies \operatorname{nullity} (\operatorname{T}) = 0

    이다. 또한 T⁡\operatorname{T} 가 전사이므로 공역과 치역이 같다. 그러므로

    rank⁡(T⁡)=dim⁡(W) \operatorname{rank} (\operatorname{T} ) = \dim (\mathbf{W} )

    이다. 그러면 차원정리 에 의하여 dim⁡(W)=dim⁡(V)\dim (\mathbf{W}) = \dim (\mathbf{V} ) 임을 알 수 있다. ■

유한차원 벡터공간 V,W\mathbf{V} , \mathbf{W} 와 선형변환 T⁡:V→W\operatorname{T} : \mathbf{V} \to \mathbf{W} 에 대하여 dim⁡(V)=dim⁡(W)\dim (\mathbf{V} ) = \dim (\mathbf{W} ) 이면 다음이 동치이다.

  • T⁡\operatorname{T} 가 단사이다.

  • T⁡\operatorname{T} 가 전사이다.

  • T⁡\operatorname{T} 가 전단사이다.

  • T⁡\operatorname{T} 가 가역이다.

  • 증명

    정리 2.5 에 의하면 같은 차원을 갖는 두 유한차원 벡터공간 사이에 정의된 선형변환에 대하여 단사, 전사가 동치이다. 이로써 전단사도 동치이며 가역도 동치이다.

Invertible matrix✔

가역행렬(invertible matrix)

n×nn \times n 행렬 AA 에 대하여 AB=BA=IAB=BA=I 인 n×nn \times n 행렬 BB 가 존재할 때 AA 를 가역이라고 한다.
  • 이는 역함수의 정의와 비슷하다. 선형변환을 행렬과 대응시키고 그 연산도 보존해보았듯이 선형변환과 행렬의 역연산도 연결시켜볼 것이다.

역행렬(inverse matrix)

AA 가 가역일때 AB=BA=IAB = BA = I 를 만족하는 행렬 BB 이다.

  • 예시

    (5723)\begin{pmatrix} 5&7\\ 2&3\\ \end{pmatrix} 의 역행렬은 (3−7−25)\begin{pmatrix} 3&-7\\ -2&5\\ \end{pmatrix} 이다.

역행렬은 유일하다.

  • 증명

    역행렬을 선형변환의 역함수와 연결시킨다면 역함수가 유일하다 는 정리로도 증명가능하다. 그러나 이 방법으로도 증명할 수 있다. AC=CA=IAC=CA = I 를 만족하는 또 다른 행렬 CC 가 존재한다면 다음이 성립한다.

    C=CI=C(AB)=(CA)B=IB=B■ C = CI = C(AB) = (CA)B = IB = B \tag*{■}

Properties of Invertibility✔

정리 2.18

유한차원 벡터공간 V,W\mathbf{V} , \mathbf{W} 와 각각의 순서기저 β,γ\beta , \gamma, 선형변환 T⁡:V→W\operatorname{T} : \mathbf{V} \to \mathbf{W} 에 대하여 다음이 성립한다.

  • T⁡\operatorname{T} 가 가역인 것과 [T⁡]βγ[\operatorname{T} ] ^{\gamma}_{\beta} 가 가역인 것은 동치이다.

  • [T⁡−1]γβ=([T⁡]βγ)−1[\operatorname{T} ^{-1}] ^{\beta }_{\gamma } = ([\operatorname{T} ] ^{\gamma}_{\beta} ) ^{-1}

  • 이 정리는 선형변환의 역함수와 행렬의 역행렬을 연결시켜준다.

  • 증명

    T⁡\operatorname{T} 가 가역이면 정리 2.17 따름정리로부터 dim⁡(V)=dim⁡(W)\dim (\mathbf{V} ) = \dim (\mathbf{W} ) 이다. n=dim⁡(V)n = \dim (\mathbf{V} ) 라고 하면 [T⁡]βγ[\operatorname{T} ] ^{\gamma}_{\beta} 는 n×nn \times n 행렬이다. 또 역함수 T⁡−1\operatorname{T} ^{-1} 에 대하여 T⁡−1T⁡=I⁡V\operatorname{T} ^{-1}\operatorname{T} = \operatorname{I} _{\mathbf{V} } 이다. 이러한 사실들과 항등변환의 행렬표현은 항등행렬이다 와 정리 2.11 에 의하여

    In=[I⁡V]β=[T⁡−1T⁡]β=[T⁡−1]γβ[T⁡]βγ I_n = [\operatorname{I} _{\mathbf{V} }] _{\beta } = [\operatorname{T} ^{-1}\operatorname{T} ] _{\beta } = [\operatorname{T} ^{-1}] ^{\beta }_{\gamma } [\operatorname{T} ]^{\gamma}_{\beta}

    이다. 같은방식으로

    In=[T⁡]βγ[T⁡−1]γβ I_n = [\operatorname{T} ]^{\gamma}_{\beta}[\operatorname{T} ^{-1}] ^{\beta }_{\gamma }

    을 얻을 수 있다. 그러므로 T⁡\operatorname{T} 가 가역임을 가정했을 때 [T⁡]βγ[\operatorname{T}]^{\gamma}_{\beta} 는 가역이고, ([T⁡]βγ)−1=[T⁡−1]γβ([\operatorname{T} ]^{\gamma}_{\beta} )^{-1} = [\operatorname{T} ^{-1}] ^{\beta }_{\gamma} 이다. ▲

    A=[T⁡]βγA = [\operatorname{T} ] ^{\gamma}_{\beta} 가 가역이면 AB=BA=InAB = BA = I_n 을 만족하는 n×nn \times n 행렬 BB 가 존재한다. 우선 γ={w1,w2,…,wn},β={v1,v2,…,vn}\gamma = \{w_1, w_2, \dots, w_n\}, \beta = \{v_1, v_2, \dots, v_n\} 이라고 하자. 그러면 정리 2.6 에 의하여

    j∈{1,2,…,n}:U⁡(wj)=∑i=1nBijvi j \in \{1,2,\dots,n\} : \operatorname{U} (w_j) = \sum_{i=1}^{n}B _{ij}v_i

    을 만족하는 선형변환 U⁡:L(W,V)\operatorname{U} : \mathcal{L}(\mathbf{W} ,\mathbf{V} ) 이 유일하게 존재한다. 이는 [U⁡]γβ=B[\operatorname{U} ] ^{\beta }_{\gamma } = B 임을 말해준다. 그러면 정리 2.11 에 의하여

    [U⁡T⁡]γ=[U⁡]γβ[T⁡]βγ=BA=In=[I⁡V]β [\operatorname{U} \operatorname{T} ] _{\gamma } = [\operatorname{U} ]^{\beta }_{\gamma } [\operatorname{T} ]^{\gamma}_{\beta} = BA = I_n = [\operatorname{I} _{\mathbf{V} }]_{\beta }

    이다. 따라서 U⁡T⁡=I⁡V\operatorname{U} \operatorname{T} = \operatorname{I} _{\mathbf{V} } 이다. 같은 방식으로 T⁡U⁡=I⁡W\operatorname{T} \operatorname{U} = \operatorname{I} _{\mathbf{W} } 를 보일 수 있다. 그러므로 [T⁡]βγ[\operatorname{T} ] ^{\gamma}_{\beta} 가 가역임을 가정했을 때 T⁡\operatorname{T} 도 가역이다. ■

정리 2.18 따름정리 1

유한차원 벡터공간 V\mathbf{V} 의 순서기저 β\beta 와 선형변환 T⁡:V→V\operatorname{T} : \mathbf{V} \to \mathbf{V} 에 대하여 다음이 성립한다.

  • T⁡\operatorname{T} 가 가역인 것과 [T⁡]β[\operatorname{T} ]_{\beta} 가 가역인 것은 동치이다.

  • [T⁡−1]β=([T⁡]β)−1[\operatorname{T} ^{-1}] _{\beta } = ([\operatorname{T} ] _{\beta} ) ^{-1}
  • 증명

정리 2.18 따름정리 2

n×nn \times n 행렬 AA 에 대하여 다음이 성립한다.

  • AA 가 가역인 것과 L⁡A\operatorname{L}_{A} 가 가역인 것은 동치이다.

  • (L⁡A)−1=L⁡A−1(\operatorname{L}_{A}) ^{-1} = \operatorname{L}_{A ^{-1}}
  • 증명

문제 2.4-4

A,BA, B 가 n×nn \times n 가역행렬이면 다음이 성립한다.

  1. ABAB 가 가역이다.

  2. (AB)−1=B−1A−1(AB) ^{-1} = B ^{-1}A ^{-1}

  • 증명

    A,BA, B 가 가역이므로 AA−1=A−1A=InA A ^{-1} = A ^{-1} A = I_n, BB−1=B−1B=InB B ^{-1} = B ^{-1} B = I_n 인 A−1,B−1A ^{-1}, B ^{-1} 가 존재한다. 정리 2.16 따름정리 에 의하여 행렬의 결합법칙이 성립하므로 다음이 성립한다.

    (AB)B−1A−1=AInA−1=In (AB) B ^{-1}A ^{-1} = AI_nA ^{-1} = I_n
    B−1A−1(AB)=BInB−1=In B ^{-1}A ^{-1} (AB) = BI_nB ^{-1} = I_n

    그러므로 ABAB 는 가역이고, (AB)−1=B−1A−1(AB) ^{-1} = B ^{-1} A ^{-1} 이다. ■

문제 2.4-5

가역행렬 AA 에 대하여 A⊤A ^{\top} 가 가역이고 (A⊤)−1=(A−1)⊤(A ^{\top}) ^{-1} = (A ^{-1}) ^{\top} 이다.

  • 증명

    AA−1=A−1A=IA A ^{-1} = A ^{-1}A = I 인 A−1A ^{-1} 가 존재한다. (AB)⊤=B⊤A⊤(AB) ^{\top} = B ^{\top} A ^{\top} 이므로 다음이 성립한다.

    (AA−1)⊤=(A−1)⊤A⊤=I(AA ^{-1}) ^{\top} = (A ^{-1}) ^{\top} A ^{\top} = I
    (A−1A)⊤=A⊤(A−1)⊤=I(A ^{-1} A ) ^{\top} = A ^{\top} (A ^{-1}) ^{\top} = I

    따라서 (A⊤)−1=(A−1)⊤(A ^{\top}) ^{-1} = (A ^{-1}) ^{\top} 이다.

문제 2.4-9

n×nn \times n 행렬 A,BA, B 에 대하여 ABAB 가 가역이면 A,BA, B 모두 가역이다.

문제 2.4-10

AB=InAB = I_n 인 n×nn \times n 행렬 A,BA, B 에 대하여 다음이 성립한다.

  1. A,BA, B 는 가역이다.

  2. A=B−1A = B ^{-1}

  • 증명

    1:

    정리 2.15 - 1 에 의하여 AB=InAB = I_n 은 L⁡AB=L⁡In\operatorname{L}_{AB} = \operatorname{L}_{I_n} 이다. 이는 정리 2.15 - 6, 7 에 의하여 L⁡AL⁡B=I⁡Fn\operatorname{L}_{A}\operatorname{L}_{B} = \operatorname{I} _{\mathbf{F} ^{n}} 가 된다. 그러므로 L⁡A\operatorname{L}_{A} 는 전사이고, L⁡B\operatorname{L}_{B} 는 단사이다. 그런데 dim⁡(Fn)=dim⁡(Fn)\dim (\mathbf{F} ^{n}) = \dim (\mathbf{F} ^{n}) 이므로 L⁡A\operatorname{L}_{A} 와 L⁡B\operatorname{L}_{B} 는 가역이다. 그러면 정리 2.18 따름정리 2 에 의하여 AA 와 BB 도 가역이다. ■

    2:

    AA 가 가역이므로 A−1A=InA ^{-1}A = I_n 인 A−1A ^{-1} 가 존재한다. 따라서 다음이 성립한다.

    AB=In⟺A−1AB=A−1⟺B=A−1 AB = I_n \iff A ^{-1}AB = A ^{-1} \iff B = A ^{-1}

Isomorphism✔

동형(isomorphic)

벡터공간 V,W\mathbf{V} , \mathbf{W} 사이에 가역인 선형변환 T⁡:V→W\operatorname{T} : \mathbf{V} \to \mathbf{W} 가 존재하면 V\mathbf{V} 와 W\mathbf{W} 를 동형이라 하고 다음과 같이 표기한다.

V≅W \mathbf{V} \cong \mathbf{W}

  • 공간 사이의 구조를 보존하는 사상이 있으면 두 공간은 동형이다. 동형인 두 공간은 구조만 봤을 때 구별하는 것이 불가능하다.

  • 예시

    F2×2\mathbf{F}^{2 \times 2} 의 원소 (abcd)\begin{pmatrix} a&b\\ c&d\\ \end{pmatrix} 를 F4\mathbf{F} ^{4} 의 원소 (a,b,c,d)(a,b,c,d) 에 대응시키면 벡터 합과 스칼라 곱이 비슷하게 작동한다. 이는 두 벡터공간이 구조적으로 동형임을 뜻하고, 그러므로 구조만 살펴봤을 때 두 공간을 구별하는 것이 불가능하다.

동형사상(isomorphism)

벡터공간 V,W\mathbf{V} , \mathbf{W} 사이에 가역인 선형변환 T⁡:V→W\operatorname{T} : \mathbf{V} \to \mathbf{W} 이다.

  • 동형사상이 정의된 두 대수구조는 본질적으로 서로 같다. 구체적으로 말하자면 서로 동형인 대상은 완전히 같은 구조와 성질을 가진다. 따라서 구조적으로만 따졌을 때 동형인 두 대상을 구분하기란 불가능하다.

  • 일반적으로 동형사상은 전단사인 준동형사상으로 설명된다. 본 정의에서는 전단사라는 조건이 가역으로, 준동형사상이라는 조건이 선형변환으로 설명된 것뿐이다.

  • 예시

    F2×2\mathbf{F}^{2 \times 2} 와 F4\mathbf{F} ^{4} 사이에 동형사상이 존재하므로 이 두 벡터공간은 동형이다. 두 공간의 구조는 동일하다.

동형은 동치관계이다.

  • 증명

    F\mathbf{F}-벡터공간을 원소로 가지는 집합족 V\mathcal{V} 의 임의의 두 원소 V,W\mathbf{V}, \mathbf{W} 가 동형이라는 것을 관계 V≅W\mathbf{V} \cong \mathbf{W} 로 표기하자. ≅\cong 이 동치관계임을 보여야 한다.

    I⁡V(x)=x\operatorname{I} _{\mathbf{V} }(x) = x 은 V→V\mathbf{V} \to \mathbf{V} 에서 정의된 가역인 선형변환이다. 그러므로 V≅V\mathbf{V} \cong \mathbf{V} 이다. ▲

    V,W∈V\mathbf{V} , \mathbf{W} \in \mathcal{V} 에 대하여 가역인 선형변환 T⁡:V→W\operatorname{T}: \mathbf{V} \to \mathbf{W} 가 정의되었다고 하자. 그러면 가역인 선형역변환 T⁡−1:W→V\operatorname{T} ^{-1} : \mathbf{W} \to \mathbf{V} 이 존재한다. 그러므로 V≅W⟹W≅V\mathbf{V} \cong \mathbf{W} \implies \mathbf{W} \cong \mathbf{V} 이다. ▲

    V,W,Z∈V\mathbf{V},\mathbf{W},\mathbf{Z}\in \mathcal{V} 에 대하여 가역인 선형변환 T⁡:V→W\operatorname{T}:\mathbf{V}\to \mathbf{W} 와 U⁡:W→Z\operatorname{U}:\mathbf{W}\to \mathbf{Z} 가 정의되었다고 하자. 두 변환의 합성 U⁡T⁡:V→Z\operatorname{U}\operatorname{T}: \mathbf{V}\to \mathbf{Z} 은 선형이고, 전단사이다. 따라서 V≅Z\mathbf{V}\cong \mathbf{Z} 이다. ■

정리 2.19

같은 체 위에서 정의된 유한차원 벡터공간 V,W\mathbf{V} , \mathbf{W} 에 대하여 다음이 성립한다.

V≅W⟺dim⁡(V)=dim⁡(W)\mathbf{V} \cong \mathbf{W} \iff \dim (\mathbf{V} ) = \dim (\mathbf{W} )

  • 이 정리는 차원이 같은 벡터공간 사이에는 동형사상이 반드시 존재한다는 것을 말해준다. 이는 차원이 같은 벡터공간은 본질적으로 서로 같음을 의미한다. 왜냐하면 동형사상이 존재하면 아무런 손실도 없이 한 벡터공간을 다른 벡터공간으로 변형시킬 수 있기 때문이다.

  • 증명

    V≅W\mathbf{V} \cong \mathbf{W} 를 가정하면 정리 2.17 따름정리 에 의하여 dim⁡(V)=dim⁡(W)\dim (\mathbf{V} ) = \dim (\mathbf{W} ) 이다. ▲

    dim⁡(V)=dim⁡(W)\dim (\mathbf{V} ) = \dim (\mathbf{W} ) 를 가정하자. 그리고 V,W\mathbf{V}, \mathbf{W} 의 각각의 기저를 β={v1,v2,…,vn},γ={w1,w2,…,wn}\beta = \{v_1, v_2, \dots, v_n \}, \gamma = \{w_1, w_2, \dots, w_n \} 라고 하자. 정리 2.6 에 의하여 T⁡(vi)=wi\operatorname{T} (v_i) = w_i 인 선형변환이 유일하게 존재한다. 정리 2.2 에 의하면

    im⁡(T⁡)=span⁡(T⁡(β))=span⁡(γ)=W \operatorname{im} (\operatorname{T}) = \operatorname{span} (\operatorname{T} (\beta )) = \operatorname{span} (\gamma ) = \mathbf{W}

    이므로 T⁡\operatorname{T} 는 전사이다. 그러면 정리 2.5 에 의하여 T⁡\operatorname{T} 는 단사이다. 그러므로 T⁡\operatorname{T} 는 동형사상이고 결국 V≅W\mathbf{V} \cong \mathbf{W} 이다. ■

  • 예시

    m×nm \times n 행렬의 벡터 공간 Rm×n\R ^{m \times n} 과 길이 mnmn 의 벡터의 벡터 공간 Rmn\R ^{mn} 사이에 동형사상이 존재한다.

두 벡터공간 V,W\mathbf{V} , \mathbf{W} 에 대하여 V≅W\mathbf{V} \cong \mathbf{W} 이면 둘 다 유한차원이거나 둘 다 무한차원이다.

정리 2.19 따름정리

F\mathbf{F}-벡터공간 V\mathbf{V} 와 Fn\mathbf{F} ^{n} 에 대하여 다음이 성립한다.

V≅Fn⟺dim⁡(V)=n \mathbf{V} \cong \mathbf{F} ^{n} \iff \dim (\mathbf{V} ) = n

Linear Map and Matrix are essentially the same✔

정리 2.20

차원이 각각 n,mn, m 이고 순서기저가 각각 β,γ\beta , \gamma 인 F\mathbf{F}-벡터공간 V,W\mathbf{V}, \mathbf{W} 에 대하여 다음과 같이 정의된 함수는 동형사상이다.

Φβγ:L(V,W)→Fm×n,T⁡↦[T⁡]βγ\Phi ^{\gamma}_{\beta} : \mathcal{L}(\mathbf{V} , \mathbf{W} ) \to \mathbf{F}^{m \times n}, \operatorname{T} \mapsto [\operatorname{T} ]^{\gamma}_{\beta}

  • 이 정리는 모든 선형변환이 유일한 행렬로 표현가능하고, 행렬 또한 유일한 선형변환으로 표현가능하다는 것을 말해준다.

    즉, 이 정리는 선형변환과 행렬은 본질적으로 같다는 것을 말해준다.

  • 증명

    정리 2.8 에 의하여 Φβγ\Phi ^{\gamma}_{\beta} 가 선형임은 쉽게 알 수 있다. ▲

    이제 Φβγ\Phi ^{\gamma}_{\beta} 가 전단사임을 보이자. 임의의 m×nm \times n 행렬마다 선형변환 T⁡:V→W\operatorname{T} : \mathbf{V} \to \mathbf{W} 가 유일하게 존재함을 보이면 된다.

    β={v1,v2,…,vn},γ={w1,w2,…,wn}\beta = \{v_1, v_2, \dots, v_n \}, \gamma = \{w_1, w_2, \dots, w_n \} 에 대하여 정리 2.6 에 의하여 다음 선형변환 T⁡:V→W\operatorname{T} : \mathbf{V} \to \mathbf{W} 이 유일하게 존재한다.

    j∈{1,2,…,n}:T⁡(vj)=∑i=1mAijwj j \in \{1,2,\dots,n\} : \operatorname{T} (v_j) = \sum_{i=1}^{m}A _{ij} w_j

    그러면 선형변환의 행렬표현 에 의하여 A=[T⁡]βγ=Φβγ(T⁡)A = [\operatorname{T}] ^{\gamma}_{\beta} = \Phi ^{\gamma}_{\beta} (\operatorname{T} ) 이다. 그러므로 Φβγ\Phi ^{\gamma}_{\beta} 은 전단사이고, 결국 동형사상이다. ■

차원이 각각 n,mn, m 인 F\mathbf{F}-벡터공간 V,W\mathbf{V}, \mathbf{W} 에 대하여 다음이 성립한다.

L(V,W)≅Fm×n \mathcal{L}(\mathbf{V} , \mathbf{W} ) \cong \mathbf{F}^{m \times n}

  • 선형 변환들로 이루어진 벡터공간과 행렬로 이루어진 벡터 공간은 본질적으로 동일하다.

  • 증명

    정리 2.20 에 의하여 주어진 두 벡터공간 사이에 동형사상이 존재한다. ■

정리 2.20 따름정리

유한차원 벡터공간 V,W\mathbf{V} , \mathbf{W} 에 대하여 dim⁡(L(V,W))=dim⁡(V)dim⁡(W)\dim (\mathcal{L}(\mathbf{V} , \mathbf{W} )) = \dim (\mathbf{V})\dim (\mathbf{W}) 이다.

  • 이 정리는 차원이 각각 n,mn,m 인 벡터공간 V,W\mathbf{V} , \mathbf{W} 에 대하여 dim⁡(L(V,W))=nm\dim (\mathcal{L}(\mathbf{V} , \mathbf{W} )) = nm 임을 말해준다.

  • 증명

    L(V,W)≅Fm×n\mathcal{L}(\mathbf{V} , \mathbf{W} ) \cong \mathbf{F}^{m \times n} 이고 dim⁡(Fm×n)=mn\dim (\mathbf{F}^{m \times n}) = mn 이다. 그러면 정리 2.19 에 의하여 증명이 끝난다. ■

Standard Representation✔

표준표현(standard representation)

체 F\mathbf{F} 위의 nn차원 벡터공간 V\mathbf{V} 의 순서기저를 β\beta 라고 하자. β\beta 에 대한 V\mathbf{V} 의 표준표현은 다음과 같은 함수이다.

ϕβ:V→Fn,x↦[x]β \phi _{\beta }: \mathbf{V} \to \mathbf{F} ^{n}, x \mapsto [x] _{\beta }

  • 이는 추상적인 벡터공간에 정의된 선형변환과 Fn→Fm\mathbf{F} ^{n}\to \mathbf{F} ^{m} 에서 정의된 선형변환의 관계를 보여준다.

  • 예시

    R2\R ^{2} 의 두 순서기저 β={e1,e2}={(1,0),(0,1)},γ={(1,2),(3,4)}\beta = \{e_1, e_2\} = \{(1, 0), (0, 1)\}, \gamma = \{(1, 2), (3, 4)\} 와 x=(1,−2)∈R2x = (1, -2) \in \R ^{2} 에 대하여 다음이 성립한다.

    ϕβ(x)=[x]β=(1−2),ϕβ(x)=[x]γ=(−52) \phi _{\beta }(x) = [x] _{\beta } = \begin{pmatrix} 1\\ -2\\ \end{pmatrix}, \phi _{\beta }(x) = [x] _{\gamma } = \begin{pmatrix} -5\\ 2\\ \end{pmatrix}

유한차원 벡터공간 V\mathbf{V} 의 순서기저 β\beta 에 대하여 ϕβ\phi _{\beta } 은 선형이다.

  • 증명

    선형변환의 성질 에 의하여 ϕβ(cx+y)=cϕβ(x)+ϕβ(y)\phi _{\beta }(cx + y) = c \phi _{\beta }(x) + \phi _{\beta }(y) 를 증명하면 된다. 이는 [cx+y]β=c[x]β+[y]β[cx + y] _{\beta } = c[x] _{\beta } + [y]_{\beta } 를 증명하는 것이다.

    x,y∈V,c∈Fx, y \in \mathbf{V}, c \in \mathbf{F} 에 대하여 β={v1,v2,…,vn}\beta = \{v_1, v_2, \dots, v_n \} 일 때 x=a1v1+a2v2+⋯+anvn,y=b1v1+b2v2+⋯+bnvnx = a_1v_1 + a_2v_2 + \dots + a_nv_n, y = b_1v_1 + b_2v_2 + \dots + b_nv_n 이면 다음이 성립한다.

    [x]β=(a1a2⋮an),[y]β=(b1b2⋮bn)⟹c[x]β+[y]β=(ca1+b1ca2+b2⋮can+bn) [x] _{\beta } = \begin{pmatrix} a_{1}\\ a_{2}\\ \vdots\\ a_{n}\\ \end{pmatrix}, [y] _{\beta } = \begin{pmatrix} b_{1}\\ b_{2}\\ \vdots\\ b_{n}\\ \end{pmatrix} \implies c[x] _{\beta } + [y] _{\beta } = \begin{pmatrix} ca_{1} + b_1\\ ca_{2} + b_2\\ \vdots\\ ca_{n} + b_n\\ \end{pmatrix}
    ϕβ(cx+y)=[cx+y]β=[(ca1+b1)v1+(ca2+b2)v2+⋯+(can+bn)vn]β=(ca1+b1ca2+b2⋮can+bn) \begin{align}\begin{split} \phi _{\beta }(cx + y) &= [cx + y] _{\beta } \\ &= [(ca_1+b_1)v_1 + (ca_2+b_2)v_2 + \dots + (ca_n+b_n)v_n] _{\beta } \\ &= \begin{pmatrix} ca_1 + b_1\\ ca_2 + b_2\\ \vdots \\ ca_n + b_n\\ \end{pmatrix}\\ \end{split}\end{align} \tag*{}
    ∴[cx+y]β=c[x]β+[y]β■ \therefore [cx + y] _{\beta } = c[x] _{\beta } + [y]_{\beta } \tag*{■}

정리 2.21

유한차원 벡터공간 V\mathbf{V} 의 순서기저 β\beta 에 대하여 ϕβ\phi _{\beta } 는 동형사상이다.

  • 증명

    β={v1,v2,…,vn}\beta = \{v_1, v_2, \dots, v_n \} 라고 하자.

    [x]β∈Fn[x] _{\beta } \in \mathbf{F} ^{n} 에 대하여 xx 가 유일하게 존재한다는 것을 보여야 한다. [x]β=(a1a2⋮an)[x] _{\beta } = \begin{pmatrix} a_{1}\\ a_{2}\\ \vdots\\ a_{n}\\ \end{pmatrix} 라고 하면 좌표벡터의 정의 에 의하여 x=∑i=1naivix = \sum_{i=1}^{n}a_iv_i 인 x∈Vx \in \mathbf{V} 가 존재한다.

    벡터 xx 의 β\beta 일차결합 표현은 정리 1.8 에 의하여 유일하다. ■

nn차원 벡터공간은 Fn\mathbf{F} ^{n} 과 동형이다.

  • 증명

    정리 2.19 따름정리와 정리 2.21 에 의하여 증명이 끝난다. ■

Relation between Linear Map and Matrix✔

그림 2.2

차원이 각각 n,mn, m 이고 순서기저가 각각 β,γ\beta, \gamma 인 벡터공간 V,W\mathbf{V} , \mathbf{W} 와 선형변환 T⁡:V→W\operatorname{T} : \mathbf{V} \to \mathbf{W} 와 행렬 A=[T⁡]βγA = [\operatorname{T} ] ^{\gamma}_{\beta} 에 대하여 다음이 성립한다. 즉, L⁡A∘ϕβ=ϕγ∘T⁡\operatorname{L}_{A} \circ \phi _{\beta } = \phi _{\gamma } \circ \operatorname{T} 이다.

V→T⁡Wϕβ↓↓ϕγFn→L⁡AFm \begin{CD} \mathbf{V} @> \operatorname{T} >> \mathbf{W} \\ @V \phi _{\beta } VV @VV \phi _{\gamma } V \\ \mathbf{F} ^{n} @> \operatorname{L}_{A} >> \mathbf{F} ^{m} \end{CD}

  • 동형사상 ϕβ\phi _{\beta } 를 통해 V\mathbf{V} 와 Fn\mathbf{F} ^{n} 을 동일시할 수 있고 동형사상 ϕγ\phi _{\gamma } 를 통해 W\mathbf{W} 와 Fm\mathbf{F} ^{m} 을 동일시할 수 있다.

    물론 T⁡\operatorname{T} 가 동형사상이면 V\mathbf{V} 와 W\mathbf{W} 을 동일시할 수 있고 L⁡A\operatorname{L}_A 가 동형사상이면 Fn\mathbf{F} ^{n} 와 Fm\mathbf{F} ^{m} 을 동일시할 수 있다.

  • 이 그림은 다루기 힘든 추상적인 두 벡터공간 사이에 정의된 연산을 우리에게 친숙한 Fn\mathbf{F} ^{n} 와 Fm\mathbf{F} ^{m} 사이에 정의된 연산으로 나타낼 수 있다는 것을 말해준다.

  • 예시

    선형변환 T⁡:P3(R)→P2(R),f(x)↦f′(x)\operatorname{T} :\mathbf{P}_{3}(\R) \to \mathbf{P}_{2}(\R), f(x) \mapsto f'(x) 에서 β,γ\beta , \gamma 를 각각 P3(R),P2(R)\mathbf{P}_{3}(\R), \mathbf{P}_{2}(\R) 의 순서기저라 하자.

    또한 ϕβ:P3(R)→R4,ϕγ:P2(R)→R3\phi _{\beta }: \mathbf{P}_{3}(\R) \to \R ^{4}, \phi _{\gamma } : \mathbf{P}_{2}(\R) \to \R ^{3} 을 각각의 기저에 대한 표준표현이라고 하자.

    T⁡\operatorname{T} 의 행렬표현은 다음과 같다.

    [T⁡]βγ=A=(010000200003) [\operatorname{T} ] ^{\gamma}_{\beta} = A = \begin{pmatrix} 0&1&0&0\\ 0&0&2&0\\ 0&0&0&3\\ \end{pmatrix}

    이제 위 그림이 말하는 L⁡A∘ϕβ=ϕγ∘T⁡\operatorname{L}_{A} \circ \phi _{\beta } = \phi _{\gamma } \circ \operatorname{T} 가 정말 성립하는지 다항식 p(x)=2+x−3x2+5x3p(x) = 2 + x - 3x ^{2} + 5x ^{3} 에 대하여 확인해보자.

    L⁡A(ϕβ(p(x)))=(010000200003)(21−35)=(1−615) \operatorname{L}_{A} (\phi _{\beta }(p(x))) = \begin{pmatrix} 0&1&0&0\\ 0&0&2&0\\ 0&0&0&3\\ \end{pmatrix} \begin{pmatrix} 2\\ 1\\ -3\\ 5\\ \end{pmatrix}=\begin{pmatrix} 1\\ -6\\ 15\\ \end{pmatrix}
    ϕγ(T(p(x)))=ϕγ(p′(x))=ϕγ(1−6x+15x2)=(1−615) \phi _{\gamma }(T(p(x))) = \phi _{\gamma }(p'(x))= \phi _{\gamma }(1-6x+15x ^{2}) = \begin{pmatrix} 1\\ -6\\ 15\\ \end{pmatrix}

문제 2.4-17

유한차원 벡터공간 V,W\mathbf{V} , \mathbf{W} 와 동형사상 T⁡:V→W\operatorname{T} : \mathbf{V} \to \mathbf{W}, V\mathbf{V} 의 부분공간 V0\mathbf{V}_0 에 대하여 다음이 성립한다.

  1. T⁡(V0)\operatorname{T} (\mathbf{V} _0) 은 W\mathbf{W} 의 부분공간이다.

  2. dim⁡(V0)=dim⁡(T⁡(V0))\dim (\mathbf{V} _0) = \dim (\operatorname{T} (\mathbf{V} _0))

  • 증명

    1:

    선형변환의 성질 에 의하여 T⁡(0)=0∈W\operatorname{T} (0) = 0 \in \mathbf{W} 이다. ▲

    x,y∈V0x, y \in \mathbf{V} _0 에 대하여 T⁡(x)∈T⁡(V0),T⁡(y)∈T⁡(V0)\operatorname{T} (x) \in \operatorname{T} (\mathbf{V} _0), \operatorname{T} (y) \in \operatorname{T} (\mathbf{V} _0) 이다. 이때 V0\mathbf{V} _0 이 부분공간이므로 x+y∈V0x + y \in \mathbf{V} _0 이다. 그러므로 T⁡(x+y)=T⁡(x)+T⁡(y)∈T⁡(V0)\operatorname{T} (x + y) = \operatorname{T} (x) + \operatorname{T} (y) \in \operatorname{T} (\mathbf{V} _0) 이다. ▲

    a∈F,x∈V0a \in \mathbf{F}, x \in \mathbf{V} _0 에 대하여 V0\mathbf{V} _0 가 부분공간이므로 ax∈V0ax \in \mathbf{V} _0 이다. 그러므로 T⁡(ax)=aT⁡(x)∈T⁡(V0)\operatorname{T} (ax) = a \operatorname{T} (x) \in \operatorname{T} (\mathbf{V} _0) 이다. ▲

    정리 1.3 에 의하여 T⁡(V0)\operatorname{T} (\mathbf{V} _0) 은 W\mathbf{W} 의 부분공간이다. ■

    2:

    변환 T⁡:V→W\operatorname{T} : \mathbf{V} \to \mathbf{W} 의 제한 T⁡∣V0:V0→T⁡(V0)\operatorname{T} | _{\mathbf{V}_0}: \mathbf{V} _0 \to \operatorname{T}(\mathbf{V} _0) 은 전사이다. 동형사상 T⁡\operatorname{T} 가 단사이므로 T⁡\operatorname{T} 의 대응규칙을 유지한채 논의영역을 축소시킨 T⁡∣V0\operatorname{T}|_{\mathbf{V} _0} 도 단사이다. 그러므로 T⁡∣V0\operatorname{T}|_{\mathbf{V} _0} 는 동형사상이며 V0≅T⁡(V0)\mathbf{V} _0 \cong \operatorname{T} (\mathbf{V} _0) 이다. 그러므로 정리 2.19 에 의하여 다음이 성립한다.

    dim⁡(V0)=dim⁡(T⁡(V0))■ \dim (\mathbf{V} _0) = \dim (\operatorname{T} (\mathbf{V} _0)) \tag*{■}

문제 2.4-20

nn차원 벡터공간 V\mathbf{V} 와 mm차원 벡터공간 W\mathbf{W}, 선형변환 T⁡:V→W\operatorname{T} : \mathbf{V} \to \mathbf{W}, V\mathbf{V} 의 순서기저 β\beta, W\mathbf{W} 의 순서기저 γ\gamma, 행렬 A=[T⁡]βγA = [\operatorname{T} ]^{\gamma}_{\beta} 에 대하여 다음이 성립한다.

  1. rank⁡(T⁡)=rank⁡(L⁡A)\operatorname{rank} (\operatorname{T} ) = \operatorname{rank} (\operatorname{L}_{A})

  2. nullity⁡(T⁡)=nullity⁡(L⁡A)\operatorname{nullity} (\operatorname{T} ) = \operatorname{nullity} (\operatorname{L}_{A})

  • 증명

    1:

    ϕβ\phi _{\beta } 가 전사이고 L⁡A∘ϕβ=ϕγ∘T⁡\operatorname{L}_{A} \circ \phi _{\beta } = \phi _{\gamma } \circ \operatorname{T} 이므로 다음을 얻는다.

    im⁡(L⁡A)=L⁡A(Fn)=L⁡Aϕβ(V)=ϕγT⁡(V)=ϕγ(im⁡(T⁡)) \operatorname{im} (\operatorname{L}_A) = \operatorname{L}_{A}(\mathbf{F} ^{n}) = \operatorname{L}_{A}\phi _{\beta }(\mathbf{V} ) = \phi _{\gamma }\operatorname{T} (\mathbf{V} ) = \phi _{\gamma }(\operatorname{im} (\operatorname{T}) )

    그러므로 ϕγ(im⁡(T⁡))=im⁡(L⁡A)\phi _{\gamma }(\operatorname{im} (\operatorname{T}) ) = \operatorname{im} (\operatorname{L} _A) 이다. im⁡(T⁡)\operatorname{im} (\operatorname{T}) 가 W\mathbf{W} 의 부분공간이고 정리 2.21 에 의하여 ϕγ\phi _{\gamma } 가 동형사상이므로 dim⁡(im⁡(T⁡))=dim⁡(im⁡(L⁡A))\dim (\operatorname{im} (\operatorname{T})) = \dim (\operatorname{im} (\operatorname{L}_A)) 이다. 그러므로 다음이 성립한다.

    rank⁡(T⁡)=rank⁡(L⁡A)■ \operatorname{rank} (\operatorname{T}) = \operatorname{rank} (\operatorname{L}_{A}) \tag*{■}

    2:

    y∈ϕβ(ker⁡(T⁡))y \in \phi _{\beta }(\ker (\operatorname{T}) ) 이면 x∈ker⁡(T⁡)x \in \ker (\operatorname{T}) 에 대하여 y=ϕβ(x)y = \phi _{\beta }(x) 이다. 그러므로 L⁡A∘ϕβ=ϕγ∘T⁡\operatorname{L}_{A} \circ \phi _{\beta } = \phi _{\gamma } \circ \operatorname{T} 와 ϕγ\phi _{\gamma } 가 선형인 것에 의하여 다음을 얻는다.

    L⁡A(y)=L⁡A(ϕβ(x))=ϕγT⁡(x)=ϕγ(0)=0 \operatorname{L}_{A}(y) = \operatorname{L}_{A}(\phi _{\beta }(x)) = \phi _{\gamma }\operatorname{T} (x) = \phi _{\gamma }(0) = 0

    즉, y∈ϕβ(ker⁡(T⁡))⟹y∈ker⁡(L⁡A)y \in \phi _{\beta }(\ker (\operatorname{T}) ) \implies y \in \ker (\operatorname{L}_A) 이므로 ϕβ(ker⁡(T⁡))⊂ker⁡(L⁡A)\phi _{\beta }(\ker (\operatorname{T}) ) \subset \ker (\operatorname{L}_A) 이다. ▲

    역으로 y∈ker⁡(L⁡A)y \in \ker (\operatorname{L}_A) 이면 L⁡A(y)=0\operatorname{L}_{A}(y) = 0 이다. ϕβ\phi _{\beta } 가 전사이므로 y=ϕβ(x)y = \phi _{\beta }(x) 인 x∈Vx \in \mathbf{V} 가 존재한다.

    만약 T⁡(x)=0\operatorname{T} (x) = 0 이라면 x∈ker⁡(T⁡)⟹y∈ϕβ(ker⁡(T⁡))x \in \ker (\operatorname{T}) \implies y \in \phi _{\beta }(\ker (\operatorname{T}) ) 이다. 그러면 y∈ker⁡(L⁡A)⟹y∈ϕβ(ker⁡(T⁡))y \in \ker (\operatorname{L}_A) \implies y \in \phi _{\beta }(\ker (\operatorname{T}) ) 이므로 ker⁡(L⁡A)⊂ϕβ(ker⁡(T⁡))\ker (\operatorname{L}_A) \subset \phi _{\beta }(\ker (\operatorname{T}) ) 이고 결국 ϕβ(ker⁡(T⁡))=ker⁡(L⁡A)\phi _{\beta }(\ker (\operatorname{T}) ) = \ker (\operatorname{L}_A) 가 된다. 그러면 ker⁡(T⁡)\ker (\operatorname{T}) 가 V\mathbf{V} 의 부분공간 이고 정리 2.21 에 의하여 ϕβ\phi _{\beta } 가 동형사상이므로 dim⁡(ker⁡(T⁡))=dim⁡(ker⁡(L⁡A))\dim (\ker (\operatorname{T}) ) = \dim (\ker (\operatorname{L}_A)) 을 얻고 모든 증명이 끝난다.

    다음이 성립한다.

    ϕγ(T⁡(x))=L⁡A(ϕβ(x))=L⁡A(y)=0 \phi _{\gamma }(\operatorname{T} (x)) = \operatorname{L}_{A}(\phi _{\beta }(x)) = \operatorname{L}_{A}(y) = 0

    ϕγ\phi _{\gamma } 가 단사이므로 정리 2.4 에 의하여 T⁡(x)=0\operatorname{T} (x) = 0 이다. ■

Change of basis✔

정리 2.22

유한차원 벡터공간 V\mathbf{V} 의 두 순서기저 β,β′\beta , \beta ' 에 대하여 Q=[I⁡V]β′βQ = [\operatorname{I} _{\mathbf{V} }] ^{\beta}_{\beta'} 라고 하면 다음이 성립한다.

  1. QQ 는 가역행렬이다.

  2. ∀v∈V:[v]β=Q[v]β′\forall v \in \mathbf{V} : [v] _{\beta } = Q[v] _{\beta '}

  • 증명

    정리 2.18 에 의하여 I⁡V\operatorname{I} _{\mathbf{V}} 가 가역이므로 QQ 도 가역이다. ▲

    정리 2.14 에 의하여 다음이 성립한다.

    ∀v∈V:[v]β=[I⁡V(v)]β=Q[v]β′■ \forall v \in \mathbf{V} : [v] _{\beta } = [\operatorname{I} _{\mathbf{V} }(v)]_{\beta} = Q[v]_{\beta '} \tag*{■}

좌표변환 행렬(change of coordinate matrix, change of basis matrix)

유한차원 벡터공간 V\mathbf{V} 의 두 순서기저 β,β′\beta , \beta ' 에 대하여 β′\beta ' 좌표를 β\beta 좌표로 변환하는 행렬 Q=[I⁡V]β′βQ = [\operatorname{I} _{\mathbf{V} }] ^{\beta}_{\beta'} 이다.

  • 예시

    R2\R ^{2} 의 서로 다른 기저 β={(1,1),(1,−1)},β′={(2,4),(3,1)}\beta = \{(1,1), (1, -1)\}, \beta ' = \{(2,4), (3,1)\} 에 대하여

    (2,4)=3(1,1)−1(1,−1) (2, 4) = 3(1, 1) - 1(1, -1)
    (3,1)=2(1,1)+1(1,−1) (3, 1) = 2(1, 1) + 1(1, -1)

    이므로 Q=(32−11)Q = \begin{pmatrix} 3&2\\ -1&1\\ \end{pmatrix} 이다. 그러므로 다음이 성립한다.

    [(2,4)]β=Q[(2,4)]β′=Q(10)=(3−1) [(2, 4)] _{\beta } = Q[(2, 4)] _{\beta '} = Q \begin{pmatrix} 1\\ 0\\ \end{pmatrix} = \begin{pmatrix} 3\\ -1\\ \end{pmatrix}

  • 이것은 벡터공간 V\mathbf{V} 의 서로 다른 기저 β′,β\beta' , \beta 와 어떤 벡터 vv 에 대하여

    v→[v]β′v→[v]β v \to [v] _{\beta' } \qquad v \to [v] _{\beta }

    와 같이 좌표벡터를 구한 것에서

    [v]β′→[v]β [v] _{\beta' } \to [v] _{\beta}

    와 같이 어떤 좌표를 다른 기저에 대한 좌표로 변환하는 수학적 장치이다.

  • 유한차원 벡터공간 V\mathbf{V} 가 차원이 nn 이고 서로 다른 기저 β′=(u1,u2,…,un),β=(w1,w2,…,wn)\beta' = (u_1, u_2, \dots, u_n), \beta = (w_1, w_2, \dots, w_n) 을 갖는다고 하자. 어떤 벡터 v∈Vv \in \mathbf{V} 가 [v]β′[v] _{\beta' } 나 [v]β[v] _{\beta} 와 같은 좌표벡터로 표현되어 있을 때 이것으로부터 어떻게 다른 기저에 대한 좌표벡터를 구할 수 있을까? 이것을 정리 2.14 를 사용하지 말고 행렬 성분을 실제로 다뤄보면서 알아보자.

    먼저 좌표벡터 의 정의에 의하여 [v]β′=(c1c2⋮cn)[v] _{\beta' }= \begin{pmatrix} c_1\\ c_2\\ \vdots \\ c_n\\ \end{pmatrix} 는 다음과 같은 기저 β′\beta' 의 일차결합이다. c1,c2,…,cnc_1, c_2, \dots, c_n 은 스칼라이다.

    v=c1u1+c2u2+⋯+cnun v = c_1u_1 + c_2u_2 + \dots + c_nu_n

    이때 기저 β′\beta' 의 벡터 u1,u2,…,unu_1, u_2, \dots, u_n 들을 다음과 같이 기저 β\beta 에 대한 좌표벡터로 나타낼 수 있다. aija_{ij} 들은 스칼라이다.

    [u1]β=(a11a21⋮an1),[u2]β=(a12a22⋮an2),…,[un]β=(a1na2n⋮ann)(1) [u_1] _{\beta} = \begin{pmatrix} a _{11}\\ a _{21}\\ \vdots\\ a _{n1}\\ \end{pmatrix}, [u_2] _{\beta} = \begin{pmatrix} a _{12}\\ a _{22}\\ \vdots\\ a _{n2}\\ \end{pmatrix}, \dots, [u_n] _{\beta} = \begin{pmatrix} a _{1n}\\ a _{2n}\\ \vdots\\ a _{nn}\\ \end{pmatrix} \tag{1}

    그러므로 β′\beta' 를 다음과 같이 β\beta 의 일차결합으로 나타낼 수 있다.

    u1=a11w1+a21w2+⋯+an1wn u_1 = a _{11}w_1+ a _{21}w_2+ \dots+ a _{n1}w_n
    u2=a12w1+a22w2+⋯+an2wn u_2 = a _{12}w_1+ a _{22}w_2+ \dots+ a _{n2}w_n
    ⋮ \vdots
    un=a1nw1+a2nw2+⋯+annwn u_n = a _{1n}w_1+ a _{2n}w_2+ \dots+ a _{nn}w_n

    그렇다면 v=c1u1+c2u2+⋯+cnunv = c_1u_1 + c_2u_2 + \dots + c_nu_n 와 같이 표현된 일차결합에서 uiu_i 들을 위와 같은 β\beta 의 일차결합 표현으로 치환해버리면 [v]β′[v] _{\beta' } 를 [v]β[v] _{\beta} 로 변환할 수 있다. 즉, 다음과 같이 vv 의 β′\beta' 일차결합 표현을 β\beta 일차결합 표현으로 변환하는 것이다.

    v=c1(a11w1+a21w2+⋯+an1wn)+c2(a12w1+a22w2+⋯+an2wn)+⋯+cn(a1nw1+a2nw2+⋯+annwn) \begin{align}\begin{split} v = \enspace & c_1(a _{11}w_1+ a _{21}w_2+ \dots+ a _{n1}w_n ) + \\ &c_2(a _{12}w_1+ a _{22}w_2+ \dots+ a _{n2}w_n ) + \\ &\dots + \\ &c_n(a _{1n}w_1+ a _{2n}w_2+ \dots+ a _{nn}w_n ) \\ \end{split}\end{align} \tag*{}
    v=(c1a11+c2a21+⋯+cnan1)w1+(c1a12+c2a22+⋯+cnan2)w2+⋯+(c1a1n+c2a2n+⋯+cnann)wn \begin{align}\begin{split} v = \enspace & (c_1a _{11}+ c_2a _{21}+ \dots+ c_na _{n1} )w_1 + \\ &(c_1a _{12}+ c_2a _{22}+ \dots+ c_na _{n2} )w_2 + \\ &\dots + \\ &(c_1a _{1n}+ c_2a _{2n}+ \dots+ c_na _{nn} )w_n \\ \end{split}\end{align} \tag*{}

    그렇다면 좌표벡터 의 정의에 의하여 다음과 같이 된다.

    [v]β=(c1a11c2a21…cnan1c1a12c2a22…cnan2⋮c1a1nc2a2n…cnann)=(a11a12…a1na21a22…a2n⋮⋮⋱⋮an1an2…ann)(c1c2⋮cn)=(a11a12…a1na21a22…a2n⋮⋮⋱⋮an1an2…ann)[v]β′ \begin{align}\begin{split} [v] _{\beta} &= \begin{pmatrix} c_1 a _{11} & c_2 a _{21} & \dots & c_n a _{n1} & \\ c_1 a _{12} & c_2 a _{22} & \dots & c_n a _{n2} & \\ \vdots \\ c_1 a _{1n} & c_2 a _{2n} & \dots & c_n a _{nn} & \\ \end{pmatrix} \\ &=\begin{pmatrix} a_{11}&a_{12}&\dots&a_{1n}\\ a_{21}&a_{22}&\dots&a_{2n}\\ \vdots& \vdots& \ddots& \vdots \\ a_{n1}&a_{n2}&\dots&a_{nn}\\ \end{pmatrix} \begin{pmatrix} c_{1}\\ c_{2}\\ \vdots\\ c_{n}\\ \end{pmatrix} \\ &= \begin{pmatrix} a_{11}&a_{12}&\dots&a_{1n}\\ a_{21}&a_{22}&\dots&a_{2n}\\ \vdots& \vdots& \ddots& \vdots \\ a_{n1}&a_{n2}&\dots&a_{nn}\\ \end{pmatrix} [v] _{\beta' } \\ \end{split}\end{align} \tag*{}

    그러면 행렬 (a11a12…a1na21a22…a2n⋮⋮⋱⋮an1an2…ann)\begin{pmatrix} a_{11}&a_{12}&\dots&a_{1n}\\ a_{21}&a_{22}&\dots&a_{2n}\\ \vdots& \vdots& \ddots& \vdots \\ a_{n1}&a_{n2}&\dots&a_{nn}\\ \end{pmatrix} 은 좌표벡터 [v]β′[v] _{\beta' } 를 [v]β[v] _{\beta} 로 변환해주는 변환행렬이 되는 것이다. 이 행렬을 AA 라고 하면 기저 β′\beta' 를 β\beta 로 변환해준다는 의미로 아래첨자를 써서 Aβ′→βA _{\beta' \to \beta} 로 표기하기도 한다. 그러면 간략하게

    [v]β=Aβ′→β[v]β′ [v] _{\beta} = A _{\beta' \to \beta}[v] _{\beta' }

    라고 표기할 수 있다.

  • 그러면 어떤 기저 β′\beta' 를 다른 기저 β\beta 로 변환해주는 행렬 Aβ′→βA _{\beta' \to \beta} 이 정말로 다음을 만족할까?

    [I⁡V]β′β=Aβ′→β(2) \boxed{[\operatorname{I} _{\mathbf{V} }] ^{\beta}_{\beta'} = A _{\beta' \to \beta}} \tag{2}

    선형변환의 행렬표현 에 의하여 [I⁡V]ββ′[\operatorname{I} _{\mathbf{V} }] ^{\beta'}_{\beta} 의 jj 열은 [I⁡V(uj)]β[\operatorname{I} _{\mathbf{V} }(u_j)] _{\beta} 인데 항등변환의 정의에 의하여 이는 곧 [uj]β[u_j] _{\beta} 가 되고 좌표벡터 의 정의와 위에서 정의했었던 (1)(1) 의하여 결국

    [uj]β=(a1ja2j⋮anj) [u_j] _{\beta} = \begin{pmatrix} a _{1j}\\ a _{2j}\\ \vdots \\ a _{nj}\\ \end{pmatrix}

    가 된다. 즉, [I⁡V]β′β[\operatorname{I} _{\mathbf{V} }] ^{\beta}_{\beta'} 의 jj 열과 Aβ′→βA _{\beta' \to \beta} 의 jj 열이 같으므로 (2)(2) 가 성립함을 알 수 있다.

유한차원 벡터공간 V\mathbf{V} 의 두 순서기저 β,β′\beta , \beta ' 에 대하여 β′\beta ' 좌표를 β\beta 좌표로 변환하는 좌표변환 행렬 Q=[I⁡V]β′βQ = [\operatorname{I} _{\mathbf{V} }] ^{\beta}_{\beta'} 에 대하여 역행렬 Q−1Q^{-1} 는 β\beta 의 좌표를 β′\beta ' 으로 변환한다.

  • 증명

    [v]β=Q[v]β′⟺Q−1[v]β=[v]β′■ [v] _{\beta } = Q[v]_{\beta '} \iff Q ^{-1} [v] _{\beta } = [v]_{\beta '} \tag*{■}

Linear Operator✔

선형연산자(linear operator)

벡터공간 V\mathbf{V} 에 대하여 V\mathbf{V} 의 선형연산자는 V→V\mathbf{V} \to \mathbf{V} 에서 정의된 선형변환이다.

정리 2.23

유한차원 벡터공간 V\mathbf{V} 의 선형연산자 T⁡\operatorname{T} 와 V\mathbf{V} 의 순서기저 β,β′\beta , \beta ' 와 β′\beta ' 좌표를 β\beta 좌표로 변환하는 좌표변환 행렬 QQ 에 대하여 다음이 성립한다.

[T⁡]β′=Q−1[T⁡]βQ [\operatorname{T} ] _{\beta '} = Q ^{-1}[\operatorname{T} ] _{\beta }Q
  • 정리 2.22 가 한 기저로 표현된 벡터를 다른 기저 표현의 벡터로 변환하는 방법을 알려주었다면, 이 정리는 한 기저로 표현된 선형변환을 다른 기저로 표현된 선형변환으로 변환하는 방법을 알려준다.

  • 증명

    항등변환 I⁡\operatorname{I} 가 T⁡=T⁡I⁡=I⁡T⁡\operatorname{T} = \operatorname{T} \operatorname{I} = \operatorname{I} \operatorname{T} 인 것과 정리 2.11 인 것으로부터 다음이 성립한다.

    Q[T⁡]β′=[I⁡]β′β[T⁡]β′β′=[I⁡T⁡]β′β=[T⁡I⁡]β′β=[T⁡]ββ[I⁡]β′β=[T⁡]βQ Q[\operatorname{T} ] _{\beta '} = [\operatorname{I} ]^{\beta}_{\beta'} [\operatorname{T} ]^{\beta'}_{\beta'} = [\operatorname{I} \operatorname{T} ]^{\beta}_{\beta'} = [\operatorname{T} \operatorname{I} ]^{\beta}_{\beta'} = [\operatorname{T} ]^{\beta}_{\beta} [\operatorname{I} ]^{\beta}_{\beta'} = [\operatorname{T} ]_{\beta }Q

    그러므로 [T⁡]β′=Q−1[T⁡]βQ[\operatorname{T} ] _{\beta '} = Q ^{-1}[\operatorname{T} ] _{\beta }Q 이다.

정리 2.23 따름정리

A∈Fn×nA \in \mathbf{F}^{n \times n} 와 Fn\mathbf{F} ^{n} 의 순서기저 γ\gamma 와 γ\gamma 의 벡터들을 열로 구성한 행렬 QQ 에 대하여 다음이 성립한다.

[L⁡A]γ=Q−1AQ [\operatorname{L}_{A}] _{\gamma } = Q ^{-1} AQ

  • 이 정리는 좌측곱변환을 임의의 기저로 표현하는 방법을 알려준다.

  • 증명

    정리 2.23 에 의하여 Fn\mathbf{F}^{n} 의 표준순서기저 β\beta 와 γ\gamma 좌표를 β\beta 좌표로 변환하는 좌표변환행렬 QQ 에 대하여 다음이 성립한다.

    [L⁡A]γ=Q−1[L⁡A]βQ [\operatorname{L}_{A}]_{\gamma } = Q ^{-1}[\operatorname{L}_{A}]_{\beta }Q

    정리 2.15-(1) 에 의하여 [L⁡A]β=A[\operatorname{L}_{A}]_{\beta} = A 이므로 다음이 성립한다.

    [L⁡A]γ=Q−1AQ▲ [\operatorname{L}_{A}]_{\gamma } = Q ^{-1}AQ \tag*{▲}

    γ={v1,v2,…,vn},vj=(a1ja2j⋮anj)\gamma = \{v_1, v_2, \dots, v_n\}, v_j = \begin{pmatrix} a_{1j}\\ a_{2j}\\ \vdots\\ a_{nj}\\ \end{pmatrix} 로 두면 다음이 성립한다.

    I⁡V(vj)=vj=a1je1+a2je2+⋯+anjen=∑i=1naijei \operatorname{I}_{\mathbf{V}}(v_j) = v_j = a_{1j} e_1 + a_{2j} e_2 + \dots + a_{nj}e_n = \sum_{i=1}^{n}a_{ij}e_i

    따라서 (Q)ij=([I⁡V]γβ)ij=aij(Q)_{ij} = ([\operatorname{I}_{\mathbf{V}}]_{\gamma }^{\beta }) _{ij} = a_{ij} 이다. 즉, QQ 는 γ\gamma 의 벡터들을 열로 구성한 행렬이다. ■

  • 예시

    다음과 같은 집합 AA 와 R3\R ^{3} 의 순서기저를 생각하자.

    A=(2101130−10),γ={(−100),(210),(111)} A = \begin{pmatrix} 2&1&0\\ 1&1&3\\ 0&-1&0\\ \end{pmatrix}, \gamma = \Bigg \{ \begin{pmatrix} -1\\ 0\\ 0\\ \end{pmatrix}, \begin{pmatrix} 2\\ 1\\ 0\\ \end{pmatrix}, \begin{pmatrix} 1\\ 1\\ 1\\ \end{pmatrix} \Bigg \}

    그러면 Q,Q−1Q, Q ^{-1} 은 다음과 같다.

    Q=(−121011001),Q−1=(−12−101−1001) Q = \begin{pmatrix} -1&2&1\\ 0&1&1\\ 0&0&1\\ \end{pmatrix}, Q ^{-1} = \begin{pmatrix} -1&2&-1\\ 0&1&-1\\ 0&0&1\\ \end{pmatrix}

    그러므로 다음이 성립한다.

    [L⁡A]γ=Q−1AQ=(028−1460−1−1) [\operatorname{L}_{A}]_{\gamma } = Q ^{-1}AQ = \begin{pmatrix} 0&2&8\\ -1&4&6\\ 0&-1&-1\\ \end{pmatrix}

Matrix Similarity✔

행렬의 닮음(matrix similarity)

A,B∈Fn×nA, B \in \mathbf{F}^{n \times n} 에 대하여 B=Q−1AQB = Q ^{-1}AQ 인 가역행렬 QQ 가 존재하면 AA 와 BB 는 서로 닮음이다.

  • 행렬의 닮음은 두 행렬이 같은 선형변환의 서로 다른 기저에 대한 행렬표현임을 나타내는 관계이다.

  • 행렬의 닮음은 동치관계이다.

정리 2.23 의 일반화

유한차원 벡터공간 V,W\mathbf{V}, \mathbf{W} 의 선형변환 T⁡:V→W\operatorname{T}: \mathbf{V} \to \mathbf{W} 와 V\mathbf{V} 의 순서기저 β,β′\beta , \beta ' 와 W\mathbf{W} 의 순서기저 γ,γ′\gamma , \gamma ' 와 β′\beta ' 좌표를 β\beta 좌표로 변환하는 좌표변환 행렬 QQ 와 γ′\gamma ' 좌표를 γ\gamma 좌표로 변환하는 좌표변환 행렬 PP 에 대하여 다음이 성립한다.

[T⁡]β′γ′=P−1[T⁡]βγQ [\operatorname{T} ] ^{\gamma'}_{\beta'} = P ^{-1}[\operatorname{T} ] ^{\gamma}_{\beta} Q

  • 증명

  • 이 정리는 서로 다른 벡터공간 V,W\mathbf{V} , \mathbf{W} 사이에 정의된 선형변환에서도 성립한다. 이 경우 V\mathbf{V} 의 기저를 바꾸듯이 W\mathbf{W} 의 기저도 바꿀 수 있다.

문제 2.5-13

유한차원 F\mathbf{F}-벡터공간 V\mathbf{V} 와 순서기저 β={x1,x2,…,xn}\beta = \{x_1, x_2, \dots, x_n\}, 가역행렬 Q∈Fn×nQ \in \mathbf{F}^{n \times n} 와 j∈{1,…,n}j \in \{1, \dots, n\} 에 대하여 xj′x'_j 를 다음과 같이 정의하자.

xj′=∑i=1nQijxi x'_j = \sum_{i=1}^{n}Q _{ij}x_i

집합 β′={x1′,x2′,…,xn′}\beta ' = \{x'_1, x'_2, \dots, x'_n\} 은 V\mathbf{V} 의 기저이고 QQ 는 β′\beta ' 좌표를 β\beta 좌표로 변환하는 좌표변환 행렬이다.

  • 증명

    ∣β′∣=n|\beta '| = n 이므로 β′\beta ' 가 일차독립임을 보이면 된다. a1,a2,…,an∈Fa_1, a_2, \dots, a_n \in \mathbf{F} 에 대하여 다음이 성립한다.

    a1x1′+a2x2′+⋯+anxn′=∑j=1najxj′=∑j=1naj(∑i=1nQijxi)=∑j=1n∑i=1najQijxi=∑i=1n∑j=1najQijxi=∑j=1najQ1jx1+∑j=1najQ2jx2+⋯+∑j=1najQnjxn=0 \begin{align}\begin{split} a_1x'_1 + a_2x'_2 + \dots + a_nx'_n &= \sum_{j=1}^{n}a_jx'_j = \sum_{j=1}^{n}a_j \bigg ( \sum_{i=1}^{n}Q _{ij}x_i\bigg ) \\ &= \sum_{j=1}^{n}\sum_{i=1}^{n}a_jQ _{ij}x_i = \sum_{i=1}^{n}\sum_{j=1}^{n}a_j Q _{ij}x_i \\ &= \sum_{j=1}^{n} a_j Q _{1j}x_1 + \sum_{j=1}^{n} a_j Q _{2j}x_2 + \dots + \sum_{j=1}^{n} a_j Q _{nj}x_n = 0 \end{split}\end{align} \tag*{}
    ⟹∑j=1najQ1j=∑j=1najQ2j=⋯=∑j=1najQnj=0(1) \implies \sum_{j=1}^{n}a_j Q _{1j} = \sum_{j=1}^{n}a_j Q _{2j} = \dots = \sum_{j=1}^{n}a_j Q _{nj} = 0 \tag{1}

    QQ 의 jj열을 QjQ_j 라 하면 Qj=(Q1jQ2j⋮Qnj)Q_j = \begin{pmatrix} Q_{1j}\\ Q_{2j}\\ \vdots \\ Q_{nj}\\ \end{pmatrix} 이다. QQ 가 가역이므로 rank⁡(Q)=n\operatorname{rank} (Q) = n 이다. 또한 랭크는 행렬의 열들의 극대 일차독립 집합의 기수를 뜻하므로 QQ 의 모든 열이 일차독립이다. 즉, 다음이 성립한다.

    ∀c1,c2,…,cn∈F:c1Q1+c2Q2+⋯+cnQn=0⟹c1=c2=⋯=c2=0 \forall c_1, c_2, \dots, c_n \in \mathbf{F} : c_1Q_1 + c_2Q_2 + \dots + c_nQ_n = 0 \implies c_1 = c_2 = \dots = c_2 = 0

    이는 다음이 성립함을 뜻한다.

    ∑i=1nciQ1i=0∧∑i=1nciQ2i=0∧⋯∧∑i=1nciQni=0⟹c1=c2=⋯=c2=0 \sum_{i=1}^{n}c_i Q _{1i} = 0 \land \sum_{i=1}^{n}c_i Q _{2i} = 0 \land \dots \land \sum_{i=1}^{n}c_i Q _{ni} = 0 \implies c_1 = c_2 = \dots = c_2 = 0

    따라서 (1)(1) 에 의하여 다음이 성립한다.

    a1=a2=⋯=an=0 a_1 = a_2 = \dots = a_n = 0

    그러므로 β′\beta ' 는 기저이다. ▲

    선형변환의 행렬표현에 의하여 다음이 성립한다는 것은 [I⁡V]β′β[\operatorname{I}_{\mathbf{V}}] _{\beta '}^{\beta } 의 ii행 jj열 성분이 QijQ _{ij} 임을 뜻한다.

    I⁡V(xj′)=xj′=∑i=1nQijxi \operatorname{I}_{\mathbf{V}}(x'_j) = x'_j = \sum_{i=1}^{n}Q _{ij}x_i

    즉, Q=[I⁡]β′βQ = [\operatorname{I}]_{\beta '} ^{\beta } 이다. 좌표변환 행렬의 정의에 의하여 QQ 는 β′\beta ' 좌표를 β\beta 좌표로 변환하는 좌표변환 행렬이다. ■

Dual Space✔

선형범함수(linear functional, linear form, one-form, covector)

F\mathbf{F}-벡터공간 V\mathbf{V} 에 대하여 V→F\mathbf{V}\to \mathbf{F} 에서 정의된 선형변환이다.
  • 체 F\mathbf{F} 는 F\mathbf{F} 에서의 1차원 벡터공간이다.

  • 예시

    V=Fn×n\mathbf{V}= \mathbf{F}^{n \times n} 에 대하여 함수 f⁡:V→F,A→tr⁡(A)\operatorname{f}: \mathbf{V}\to \mathbf{F}, A \to \operatorname{tr} (A) 는 선형범함수이다.

Coordinate Function✔

좌표함수(coordinate function)

순서기저 β={x1,x2,…,xn}\beta = \{x_1, x_2, \dots, x_n\} 를 가지는 유한차원 벡터공간 V\mathbf{V} 와 i∈{1,…,n}i \in \{1,\dots,n\} 에 대하여 다음과 같이 정의된 함수 f⁡i:V→F\operatorname{f}_i: \mathbf{V}\to \mathbf{F} 를 기저 β\beta 에 대한 ii번째 좌표함수라 한다.

x∈V:[x]β=(a1a2⋮an)⟹f⁡i(x)=ai x \in \mathbf{V} : [x] _{\beta } = \begin{pmatrix} a_{1}\\ a_{2}\\ \vdots\\ a_{n}\\ \end{pmatrix} \implies \operatorname{f}_i(x) = a_i

  • 좌표함수는 V\mathbf{V} 의 선형범함수이다.

  • f⁡i(xj)=δij\operatorname{f}_i(x_j) = \delta _{ij} 이다.

쌍대공간(dual space)

F\mathbf{F}-벡터공간 V\mathbf{V} 에 대한 벡터공간 V∗:=L(V,F)\mathbf{V}^{*} := \mathcal{L}(\mathbf{V},\mathbf{F}) 를 V\mathbf{V} 의 쌍대공간이라 한다.
  • V∗\mathbf{V}^{*} 은 함수의 합과 스칼라곱 이 정의된 V\mathbf{V} 의 모든 선형범함수로 이루어진 벡터공간이다.

유한차원 벡터공간 V\mathbf{V} 와 쌍대공간 V∗\mathbf{V}^{*} 에 대하여 다음이 성립한다.

V≅V∗ \mathbf{V} \cong \mathbf{V}^{*}

  • 증명

    F\mathbf{F} 는 1차원 벡터공간이므로 dim⁡(F)=1\dim (\mathbf{F}) = 1 이다. 따라서 정리 2.20 따름정리 에 의하여 다음이 성립한다.

    dim⁡(V∗)=dim⁡(L(V,F))=dim⁡(V)dim⁡(F)=dim⁡(V) \dim (\mathbf{V}^{*}) = \dim (\mathcal{L}(\mathbf{V}, \mathbf{F})) = \dim (\mathbf{V}) \dim (\mathbf{F}) = \dim (\mathbf{V})

    정리 2.19 에 의하여 V\mathbf{V} 와 V∗\mathbf{V}^{*} 은 동형이다. ■

Double Dual✔

이중 쌍대공간(double dual)

벡터공간 V\mathbf{V} 의 쌍대공간 V∗\mathbf{V}^{*} 의 쌍대공간 V∗∗\mathbf{V}^{**} 을 V\mathbf{V} 의 이중 쌍대공간이라 한다.

정리 2.24

순서기저 β={x1,x2,…,xn}\beta = \{x_1, x_2, \dots, x_n \} 을 가지는 유한차원 벡터공간 V\mathbf{V} 와 β\beta 의 ii번째 좌표함수 f⁡i\operatorname{f}_i 에 대하여 β∗={f⁡1,f⁡2,…,f⁡n}\beta ^{*} = \{\operatorname{f}_1, \operatorname{f}_2, \dots, \operatorname{f}_n \} 는 V∗\mathbf{V}^{*} 의 순서기저이다. 즉, 다음이 성립한다.

∀f⁡∈V∗:f⁡=∑i=1nf⁡(xi)f⁡i \forall \operatorname{f} \in \mathbf{V}^{*} : \operatorname{f} = \sum_{i=1}^{n}\operatorname{f}(x_i)\operatorname{f}_i

  • 증명

    dim⁡(V∗)=n\dim (\mathbf{V}^{*}) = n 이므로 다음과 같이 β∗\beta ^{*} 가 V∗\mathbf{V}^{*} 을 생성함을 보이면 증명이 끝난다.

    ∀f⁡∈V∗:f⁡=∑i=1nf⁡(xi)f⁡i \forall \operatorname{f}\in \mathbf{V}^{*} : \operatorname{f} = \sum_{i=1}^{n}\operatorname{f}(x_i)\operatorname{f}_i

    g⁡=∑i=1nf⁡(xi)f⁡i\displaystyle \operatorname{g} = \sum_{i=1}^{n}\operatorname{f}(x_i)\operatorname{f}_i 로 두면 j∈{1,…,n}j \in \{1,\dots,n\} 에 대하여 함수의 합의 정의 에 의하여 다음이 성립한다.

    g⁡(xj)=(∑i=1nf⁡(xi)f⁡i)(xj)=∑i=1nf⁡(xi)f⁡i(xj)=∑i=1nf⁡(xi)δij=f⁡(xj) \begin{align}\begin{split} \operatorname{g}(x_j) &= \bigg (\sum_{i=1}^{n}\operatorname{f}(x_i)\operatorname{f}_i \bigg )(x_j) = \sum_{i=1}^{n}\operatorname{f}(x_i)\operatorname{f}_i(x_j) \\ &= \sum_{i=1}^{n}\operatorname{f}(x_i)\delta _{ij} = \operatorname{f}(x_j)\\ \end{split}\end{align} \tag*{}

    정리 2.6 따름정리에 의하여 f⁡=g⁡\operatorname{f} = \operatorname{g} 이다. ■

Dual Basis✔

쌍대기저(dual basis)

순서기저 β={x1,x2,…,xn}\beta = \{x_1, x_2, \dots, x_n \} 을 가지는 유한차원 벡터공간 V\mathbf{V} 와 i,j∈{1,…,n}i, j \in \{1,\dots,n\} 에 대하여 f⁡i(xj)=δij\operatorname{f}_i(x_j) = \delta _{ij} 를 만족하는 V∗\mathbf{V}^{*} 의 순서기저 β∗={f⁡1,f⁡2,…,f⁡n}\beta ^{*} = \{\operatorname{f}_1, \operatorname{f}_2, \dots, \operatorname{f}_n \} 를 β\beta 의 쌍대기저라고 한다.

  • 순서기저 β\beta 의 원소 xjx_j 에 대하여 f⁡i(xj)=δij\operatorname{f}_i(x_j) = \delta _{ij} 인 것은 좌표함수라는 뜻이다. 따라서 쌍대기저의 정의는 정리 2.24 에서의 집합 β∗\beta ^{*} 와 같다.

    또한 정리 2.24 는 쌍대기저 β∗\beta ^{*} 의 존재성을 보장해준다.

    쌍대기저의 존재성이 보장된 것을 기반으로 이 쌍대기저의 정의는 정리 2.24 에서 말하는 쌍대공간 V∗\mathbf{V}^{*} 의 기저를 구하는 방법을 알려준다. 아래 예시를 보자.

  • 예시

    벡터공간 R2\R ^{2} 의 순서기저 β={(2,1),(3,1)}\beta = \{(2,1), (3,1)\} 에 대한 β\beta 의 쌍대기저 β∗={f⁡1,f⁡2}\beta ^{*}=\{\operatorname{f}_1, \operatorname{f}_2\} 를 구해보자.

    1=f⁡1(2,1)=f⁡1(2e1+e2)=2f⁡1(e1)+f⁡1(e2) 1 = \operatorname{f}_1(2, 1) = \operatorname{f}_1(2e_1 + e_2) = 2 \operatorname{f}_1(e_1) + \operatorname{f}_1(e_2)
    0=f⁡1(3,1)=f⁡1(3e1+e2)=3f⁡1(e1)+f⁡1(e2) 0 = \operatorname{f}_1(3, 1) = \operatorname{f}_1(3e_1 + e_2) = 3 \operatorname{f}_1(e_1) + \operatorname{f}_1(e_2)

    연립방정식을 풀면 f⁡1(e1)=−1,f⁡1(e2)=3\operatorname{f}_{1}(e_1) = -1, \operatorname{f}_{1}(e_2) = 3 을 얻는다. 따라서 f⁡1(x,y)=−x+3y\operatorname{f}_{1}(x, y) = -x + 3y 이다. 같은 방식으로 f⁡2(x,y)=x−2y\operatorname{f}_{2}(x,y)=x-2y 를 얻을 수 있다.

Transpose of Linear Map✔

정리 2.25

F\mathbf{F}-벡터공간 V\mathbf{V} 와 W\mathbf{W} 의 각각의 순서기저 β,γ\beta , \gamma 와 선형변환 T⁡:V→W\operatorname{T}: \mathbf{V}\to \mathbf{W} 에 대하여 다음을 만족하는 함수 T⁡⊤:W∗→V∗\operatorname{T}^{\top}: \mathbf{W}^{*}\to \mathbf{V}^{*} 를 가정하자.

∀g⁡∈W∗:T⁡⊤(g⁡)=g⁡T⁡ \forall \operatorname{g}_{} \in \mathbf{W}^{*} : \operatorname{T}^{\top}(\operatorname{g}_{}) = \operatorname{g}_{}\operatorname{T}

함수 T⁡⊤\operatorname{T}^{\top} 는 선형변환이고, [T⁡⊤]γ∗β∗=([T⁡]βγ)⊤[\operatorname{T}^{\top}]^{\beta ^{*}}_{\gamma ^{*}} = ([\operatorname{T}]^{\gamma}_{\beta} )^{\top} 를 만족한다.

  • 정리 2.20 은 선형변환 T⁡\operatorname{T} 에 대응하는 행렬 A=[T⁡]βγA = [\operatorname{T}]^{\gamma}_{\beta} 가 존재함을 말해준다. 이 정리는 A⊤A ^{\top} 에 대응하는 선형변환이 무엇인지 알려준다.

  • 증명

    g⁡∈W∗\operatorname{g}_{}\in \mathbf{W}^{*} 는 W→F\mathbf{W}\to \mathbf{F} 에서 정의된 선형변환이다. 따라서 T⁡⊤(g⁡)=g⁡T⁡:V→F\operatorname{T}^{\top}(\operatorname{g}_{})=\operatorname{g}_{}\operatorname{T}:\mathbf{V}\to \mathbf{F} 는 V\mathbf{V} 의 선형범함수이다. 그러므로 g⁡T⁡∈V∗\operatorname{g}_{}\operatorname{T}\in \mathbf{V}^{*} 이다. 따라서 T⁡⊤\operatorname{T}^{\top} 는 W∗→T⁡∗\mathbf{W}^{*}\to \operatorname{T}^{*} 에서 정의된 함수이다. ▲

    이제 T⁡⊤\operatorname{T}^{\top} 가 선형인지 확인하자. 먼저 T⁡⊤\operatorname{T}^{\top} 의 정의에 의하여 다음이 성립한다.

    T⁡⊤(cg⁡1+g⁡2)=(cg⁡1+g⁡2)∘T⁡ \operatorname{T}^{\top}(c \operatorname{g}_{1} + \operatorname{g}_{2})= (c \operatorname{g}_{1} + \operatorname{g}_{2}) \circ \operatorname{T}

    그러면 g⁡1,g⁡2∈W∗\operatorname{g}_{1}, \operatorname{g}_{2}\in \mathbf{W}^{*} 에 대하여 함수의 합과 스칼라 곱의 정의에 의하여 다음이 성립한다.

    (cg⁡1+g⁡2)∘T⁡(x)=(cg⁡1+g⁡2)(T⁡(x))=(cg⁡1)(T⁡(x))+(g⁡2)(T⁡(x))=c(g⁡1)(T⁡(x))+(g⁡2)(T⁡(x))=c(g⁡1T⁡)(x)+(g⁡2T⁡)(x)=c(T⁡⊤(g⁡1))(x)+(T⁡⊤(g⁡2))(x) \begin{align}\begin{split} (c \operatorname{g}_{1} + \operatorname{g}_{2}) \circ \operatorname{T}(x) &= (c \operatorname{g}_{1} + \operatorname{g}_{2}) (\operatorname{T}(x)) \\ &= (c \operatorname{g}_{1})(\operatorname{T}(x)) + (\operatorname{g}_{2}) (\operatorname{T}(x)) \\ &= c (\operatorname{g}_{1})(\operatorname{T}(x)) + (\operatorname{g}_{2}) (\operatorname{T}(x)) \\ &= c (\operatorname{g}_{1} \operatorname{T})(x) + (\operatorname{g}_{2}\operatorname{T})(x) \\ &= c (\operatorname{T}^{\top}(\operatorname{g}_{1})) (x) + (\operatorname{T}^{\top}(\operatorname{g}_{2}))(x) \\ \end{split}\end{align} \tag*{}

    그러므로 함수의 합과 스칼라 곱의 정의에 의하여 다음이 성립한다. 따라서 T⁡⊤\operatorname{T}^{\top} 는 선형이다.

    T⁡⊤(cg⁡1+g⁡2)=(cg⁡1+g⁡2)∘T⁡=c(T⁡⊤(g⁡1))+(T⁡⊤(g⁡2))▲ \operatorname{T}^{\top}(c \operatorname{g}_{1} + \operatorname{g}_{2})= (c \operatorname{g}_{1} + \operatorname{g}_{2}) \circ \operatorname{T} = c (\operatorname{T}^{\top}(\operatorname{g}_{1})) + (\operatorname{T}^{\top}(\operatorname{g}_{2})) \tag*{▲}

    순서기저를 β={x1,x2,…,xn}\beta = \{x_1, x_2, \dots, x_n \}, γ={y1,y2,…,ym}\gamma = \{y_1, y_2, \dots, y_m\} 으로 두고 각각의 쌍대기저를 β∗={f⁡1,f⁡2,…,f⁡n},γ∗={g⁡1,g⁡2,…,g⁡m}\beta ^{*} = \{\operatorname{f}_{1}, \operatorname{f}_{2}, \dots, \operatorname{f}_{n}\}, \gamma ^{*}= \{\operatorname{g}_{1}, \operatorname{g}_{2}, \dots, \operatorname{g}_{m}\} 로 두고 A=[T⁡]βγA = [\operatorname{T}]^{\gamma}_{\beta} 로 두자. 선형변환의 행렬표현을 구하기 위하여 [T⁡⊤]γ∗β∗[\operatorname{T}^{\top}]^{\beta ^{*}}_{\gamma ^{*}} 의 jj 열을 구하기 위해 T⁡⊤(g⁡j)\operatorname{T}^{\top}(\operatorname{g}_{j}) 를 β∗\beta ^{*} 의 일차결합으로 나타내자. g⁡jT⁡:V→F∈V∗\operatorname{g}_{j}\operatorname{T}: \mathbf{V}\to \mathbf{F}\in \mathbf{V}^{*} 이므로 정리 2.24 에 의하여 다음이 성립한다.

    T⁡⊤(g⁡j)=g⁡jT⁡=∑s=1n(g⁡jT⁡)(xs)f⁡s \operatorname{T}^{\top}(\operatorname{g}_{j}) = \operatorname{g}_{j}\operatorname{T} = \sum_{s=1}^{n}(\operatorname{g}_{j}\operatorname{T})(x_s)\operatorname{f}_{s}

    [T⁡⊤]γ∗β∗[\operatorname{T}^{\top}]^{\beta ^{*}}_{\gamma ^{*}} 의 jj 열은 [T⁡⊤(g⁡j)]β∗[\operatorname{T}^{\top}(\operatorname{g}_{j})]_{\beta ^{*}} 이다. 따라서 ii행 jj열의 성분은 s=is = i 일 때 β∗\beta ^{*} 의 ii번째 순서기저 f⁡i\operatorname{f}_{i} 를 제외한 스칼라 (g⁡jT⁡)(xi)(\operatorname{g}_{j}\operatorname{T})(x_i) 이다. 이때 선형변환의 행렬표현 에 의하여 다음이 성립한다.

    (g⁡jT⁡)(xi)=g⁡j(T⁡(xi))=g⁡j(∑k=1mAkiyk)=∑k=1mAkig⁡j(yk)=∑k=1mAkiδjk=Aji \begin{align}\begin{split} (\operatorname{g}_{j}\operatorname{T})(x_i) = \operatorname{g}_{j}(\operatorname{T}(x_i))&=\operatorname{g}_{j}\bigg (\sum_{k=1}^{m}A _{ki}y _{k} \bigg ) \\ &= \sum_{k=1}^{m}A _{ki}\operatorname{g}_{j}(y_k) = \sum_{k=1}^{m}A _{ki}\delta _{jk}=A _{ji} \\ \end{split}\end{align} \tag*{}

    따라서 [T⁡⊤]γ∗β∗=A⊤[\operatorname{T}^{\top}]^{\beta ^{*}}_{\gamma ^{*}} = A ^{\top} 이다. ■

선형변환의 전치(transpose of linear map)

F\mathbf{F}-벡터공간 V\mathbf{V} 와 W\mathbf{W} 의 각각의 순서기저 β,γ\beta , \gamma 와 선형변환 T⁡:V→W\operatorname{T}: \mathbf{V}\to \mathbf{W} 에 대하여 다음을 만족하는 선형변환 T⁡⊤:W∗→V∗\operatorname{T}^{\top}: \mathbf{W}^{*}\to \mathbf{V}^{*} 를 T⁡\operatorname{T} 의 전치라 한다.

∀g⁡∈W∗:T⁡⊤(g⁡)=g⁡T⁡ \forall \operatorname{g}_{} \in \mathbf{W}^{*} : \operatorname{T}^{\top}(\operatorname{g}_{}) = \operatorname{g}_{}\operatorname{T}

  • 이렇게 정의한 T⁡⊤\operatorname{T}^{\top} 가 ([T⁡]βγ)⊤=[T⁡⊤]γ∗β∗([\operatorname{T}]^{\gamma}_{\beta} )^{\top} = [\operatorname{T}^{\top}]^{\beta ^{*}}_{\gamma ^{*}} 를 만족하기 때문에 선형변환의 전치라고 부른다.

  • 예시

    선형변환 T⁡:P1(R)→R2\operatorname{T}: \mathbf{P}_{1}(\R)\to \R ^{2} 를 T⁡(p(x))=(p(0),p(2))\operatorname{T}(p(x)) = (p(0), p(2)) 로 정의하자. P1(R)\mathbf{P}_{1}(\R) 의 표준순서기저 β\beta 와 R2\R ^{2} 의 표준순서기저 γ\gamma 에 대하여 [T⁡]βγ=(1012)[\operatorname{T}]^{\gamma}_{\beta} =\begin{pmatrix} 1&0\\ 1&2\\ \end{pmatrix} 이다. 이제 [T⁡⊤]γ∗β∗[\operatorname{T}^{\top}]^{\beta^{*}}_{\gamma^{*}} 를 구해보자.

    β∗={f⁡1,f⁡2}\beta ^{*}=\{\operatorname{f}_{1},\operatorname{f}_{2}\} 와 γ∗={g⁡1,g⁡2}\gamma ^{*}=\{\operatorname{g}_{1}, \operatorname{g}_{2}\} 에 대하여 [T⁡⊤]γ∗β∗=(abcd)[\operatorname{T}^{\top}]^{\beta^{*}}_{\gamma^{*}} = \begin{pmatrix} a&b\\ c&d\\ \end{pmatrix} 로 두면 선형변환의 행렬표현에 의하여 다음이 성립한다.

    T⁡⊤(g⁡1)=af⁡1+cf⁡2\operatorname{T}^{\top}(\operatorname{g}_{1}) = a \operatorname{f}_{1} + c \operatorname{f}_{2}
    T⁡⊤(g⁡2)=bf⁡1+df⁡2\operatorname{T}^{\top}(\operatorname{g}_{2}) = b \operatorname{f}_{1} + d \operatorname{f}_{2}

    β={1,x}\beta = \{1, x\} 이므로 f⁡1(1)=1,f⁡2(1)=0,f⁡1(x)=0,f⁡2(x)=1\operatorname{f}_{1}(1) = 1, \operatorname{f}_{2}(1) = 0, \operatorname{f}_{1}(x) = 0, \operatorname{f}_{2}(x) = 1 이다. 따라서 다음이 성립한다.

    T⁡⊤(g⁡1)(1)=(af⁡1+cf⁡2)(1)=af⁡1(1)+cf⁡2(1)=a⋅1+c⋅0=a \operatorname{T}^{\top}(\operatorname{g}_{1})(1) = (a \operatorname{f}_{1}+ c \operatorname{f}_{2})(1) = a \operatorname{f}_{1}(1) + c \operatorname{f}_{2}(1) = a \cdot 1 + c \cdot 0 = a

    또한 γ={(1,0),(0,1)}\gamma = \{(1, 0), (0, 1)\} 이므로 g⁡1(1,0)=1g⁡2(1,0)=0,g⁡1(0,1)=0,g⁡2(0,1)=1\operatorname{g}_{1}(1, 0) = 1 \operatorname{g}_{2}(1, 0) = 0, \operatorname{g}_{1}(0, 1) = 0, \operatorname{g}_{2}(0, 1) = 1 이다. 따라서 다음이 성립한다.

    (T⁡⊤(g⁡1))(1)=g⁡1(T⁡(1))=g⁡1(1,1)=g⁡1(e1)+g⁡1(e2)=1 (\operatorname{T}^{\top}(\operatorname{g}_{1}))(1) = \operatorname{g}_{1}(\operatorname{T}(1)) = \operatorname{g}_{1}(1,1) = \operatorname{g}_{1}(e_1) + \operatorname{g}_{1}(e_2) = 1

    즉, a=1a = 1 이다. 같은 논리로 c=0,b=1,d=2c = 0, b = 1, d = 2 를 얻는다. 결국 [T⁡⊤]γ∗β∗=(1102)=([T⁡]βγ)⊤[\operatorname{T}^{\top}]^{\beta ^{*}}_{\gamma ^{*}} = \begin{pmatrix} 1&1\\ 0&2\\ \end{pmatrix} = ([\operatorname{T}]^{\gamma}_{\beta} )^{\top} 를 직접 계산으로 확인하였다. 이는 본 정리와 같은 결과이다.

정리 2.25 보조정리

유한차원 벡터공간 V\mathbf{V} 와 벡터 x∈Vx \in \mathbf{V} 와 f⁡∈V∗\operatorname{f}_{}\in \mathbf{V}^{*} 에 대하여 함수 x^:V∗→F\hat{x}: \mathbf{V}^{*}\to \mathbf{F} 를 x^(f⁡)=f⁡(x)\hat{x}(\operatorname{f}_{}) = \operatorname{f}_{}(x) 라 정의하면 다음이 성립한다.

x^(f⁡)=0⟹x=0 \hat{x}(\operatorname{f}_{}) = 0 \implies x = 0

  • x^\hat{x} 이 V∗\mathbf{V}^{*} 의 선형범함수라는 것은 쉽게 확인할 수 있다. 즉, x^∈V∗∗\hat{x} \in \mathbf{V}^{**} 이다.

  • 증명

    대우명제 x≠0⟹x^(f⁡)=0x \neq 0 \implies \hat{x}(\operatorname{f}_{}) = 0 를 보여도 된다. 즉, x≠0x \neq 0 일 때 x^(f⁡)≠0\hat{x}(\operatorname{f}_{}) \neq 0 인 f⁡∈V∗\operatorname{f}_{}\in \mathbf{V}^{*} 가 존재함을 보이면 된다.

    x1=xx_1 = x 인 V\mathbf{V} 의 순서기저 β={x1,x2,…,xn}\beta = \{x_1, x_2, \dots, x_n \} 가 존재한다. 정리 2.24 는 기저 β\beta 에 따른 쌍대기저 β∗={f⁡1,f⁡2,…,f⁡n}\beta ^{*} = \{\operatorname{f}_{1}, \operatorname{f}_{2}, \dots, \operatorname{f}_{n}\} 의 존재를 보장해준다. f⁡1(x1)=δ11=1≠0\operatorname{f}_{1}(x_1) = \delta _{11} = 1 \neq 0 이다. f⁡1=f⁡\operatorname{f}_{1} = \operatorname{f}_{} 로 두면 증명이 끝난다. ■

    • x1=xx_1 = x 인 순서기저 β\beta 의 존재성을 보장하는 정리가 존재하지 않는다. 증명을 보완해야 함. 하지만 not now..

정리 2.26

유한차원 벡터공간 V\mathbf{V} 와 x∈Vx \in \mathbf{V} 와 f⁡∈V∗\operatorname{f}_{}\in \mathbf{V}^{*} 에 대한 함수 x^:V∗→F,f⁡→f⁡(x)\hat{x}: \mathbf{V}^{*}\to \mathbf{F}, \operatorname{f}_{} \to \operatorname{f}_{}(x) 에 대하여 함수 ψ:V→V∗∗\psi : \mathbf{V}\to \mathbf{V}^{**} 를 ψ(x)=x^\psi (x) = \hat{x} 으로 정의하면 ψ\psi 는 동형사상이다.

  • 이 정리가 보여주는 xx 와 x^\hat{x} 사이의 대응으로 유한차원 벡터공간 V\mathbf{V} 와 이중 쌍대공간 V∗∗\mathbf{V}^{**} 을 동일화하는 방법을 찾을 수 있다. 이는 두 벡터공간의 기저와 관계없이 V\mathbf{V} 와 V∗∗\mathbf{V}^{**} 사이의 동형사상이 존재함을 뜻한다.

  • 증명

    x,y∈V,c∈Fx, y \in \mathbf{V}, c \in \mathbf{F} 와 임의의 f⁡∈V∗\operatorname{f}_{}\in \mathbf{V}^{*} 에 대하여 함수의 합의 정의 에 의하여 다음이 성립한다.

    ψ(cx+y)(f⁡)=f⁡(cx+y)=cf⁡(x)+f⁡(y)=cx^(f⁡)+y^(f⁡)=(cx^+y^)(f⁡) \begin{align}\begin{split} \psi (cx+y)(\operatorname{f}_{})&= \operatorname{f}_{}(cx+y) = c \operatorname{f}_{}(x) + \operatorname{f}_{}(y) = c \hat{x}(\operatorname{f}_{})+ \hat{y}(\operatorname{f}_{}) \\ &= (c \hat{x}+ \hat{y})(\operatorname{f}_{})\\ \end{split}\end{align} \tag*{}

    즉, ψ(cx+y)=cx^+y^=cψ(x)+ψ(y)\psi (cx + y) = c \hat{x} + \hat{y} = c \psi (x) + \psi (y) 이다. 따라서 ψ\psi 는 선형이다. ▲

    x∈Vx \in \mathbf{V} 에 대하여 ψ(x)∈V∗∗\psi (x) \in \mathbf{V}^{**} 를 V∗→F,x^(f⁡)↦0\mathbf{V}^{*}\to \mathbf{F}, \hat{x}(\operatorname{f}_{}) \mapsto 0 으로 두자. 그러면 임의의 f⁡∈V∗\operatorname{f}_{}\in \mathbf{V}^{*} 에 대하여 x^(f⁡)=0\hat{x}(\operatorname{f}_{}) = 0 이다. 정리 2.25 보조정리에 의하여 x=0x = 0 를 얻는다. 이는 ker⁡(ψ)={0}\ker (\psi ) = \{0\} 을 뜻한다. 정리 2.4 에 의하여 ψ\psi 는 단사이다. ▲

    ψ\psi 가 단사이므로 정리 2.5 에 의하여 ψ\psi 는 가역이다. 또한 dim⁡(V)=dim⁡(V∗∗)\dim (\mathbf{V}) = \dim (\mathbf{V}^{**}) 이므로 ψ\psi 는 동형사상이다. ■

유한차원 벡터공간 V,W\mathbf{V}, \mathbf{W} 에 대하여 동형사상 ψ1:V→V∗∗,x↦x^\psi_1 : \mathbf{V}\to \mathbf{V}^{**}, x \mapsto \hat{x} 과 동형사상 ψ2:W→W∗∗,x↦x^\psi _2: \mathbf{W}\to \mathbf{W}^{**}, x \mapsto \hat{x} 을 정의하고, T⁡:V→W\operatorname{T}: \mathbf{V}\to \mathbf{W} 가 선형일 때 T⁡tt=(T⁡⊤)⊤\operatorname{T}^{tt}=(\operatorname{T}^{\top})^{\top} 라 정의하면 다음과 같이 ψ2T⁡=T⁡ttψ1\psi _2 \operatorname{T}= \operatorname{T}^{tt}\psi _1 가 성립한다.

V→T⁡Wψ1↓↓ψ2V∗∗→T⁡ttW∗∗ \begin{CD} \mathbf{V} @> \operatorname{T} >> \mathbf{W} \\ @V \psi _{1} VV @VV \psi _{2} V \\ \mathbf{V} ^{**} @> \operatorname{T}^{tt} >> \mathbf{W}^{**} \end{CD}

  • 동형사상 ψ1,ψ2\psi _1, \psi _2 는 정리 2.26 과 같이 정의된 것이다.

  • 증명

정리 2.26 따름정리

유한차원 벡터공간 V\mathbf{V} 와 쌍대공간 V∗\mathbf{V}^{*} 에 대하여 V∗\mathbf{V}^{*} 의 모든 순서기저는 V\mathbf{V} 의 어떤 기저의 쌍대기저이다.

  • 증명

    먼저 x∈Vx \in \mathbf{V} 와 f⁡∈V∗\operatorname{f}_{}\in \mathbf{V}^{*} 에 대한 함수 x^:V∗→F,f⁡→f⁡(x)\hat{x}: \mathbf{V}^{*}\to \mathbf{F}, \operatorname{f}_{} \to \operatorname{f}_{}(x) 를 정의하자. V∗\mathbf{V}^{*} 의 순서기저를 {f⁡1,f⁡2,…,f⁡n}\{\operatorname{f}_{1}, \operatorname{f}_{2}, \dots, \operatorname{f}_{n}\} 으로 두자.

    정리 2.24 와 정리 2.26 에 의하여 V∗\mathbf{V}^{*} 의 기저와 i,j∈{1,…,n}i, j \in \{1, \dots, n\} 에 대하여 δij=xi^(f⁡i)=f⁡j(xi)\delta _{ij} = \hat{x_i}(\operatorname{f}_{i}) = \operatorname{f}_{j}(x_i) 인 쌍대기저 {x^1,x^2,…,x^n}⊂V∗∗\{\hat{x}_1, \hat{x}_2, \dots, \hat{x}_n\} \subset \mathbf{V}^{**} 가 존재한다. 쌍대기저의 정의 에 의하여 {f⁡1,f⁡2,…,f⁡n}\{\operatorname{f}_{1}, \operatorname{f}_{2}, \dots, \operatorname{f}_{n}\} 는 {x1,x2,…,xn}\{x_1, x_2, \dots, x_n\} 의 쌍대기저이다. ■

        Friedberg, S. H., Insel, A. J., & Spence, L. E. (2018). Linear algebra. Pearson.