연산

Contents

Summation✔

Summation

Summation 은 수열 $g(i)$ 의 덧셈으로써 다음과 같이 재귀적으로 정의된다.

\sum_{i=a}^{b}g(i) = \begin{cases} 0 & b < a\\ g(b) + \displaystyle \sum_{i=a}^{b-1}g(i) & b \geq a\\ \end{cases}

수열은 숫자, 함수, 벡터, 행렬, 다항식 등 임의의 타입의 수학적 대상들로 구성 될 수 있다.
무한수열의 Summation 을 series 라고 한다.
쉽게 말해 Summation 은 다음과 같다.

$\sum_{i=m}^{n}a_i = a_m + a _{m+1} + \dots + a _{n-1} + a_n$

$i$ 를 summation 의 index 라고 한다. $m$ 을 summation 의 하계(lower bound)라고 하고, $n$ 을 summation 의 상계(upper bound)라고 한다.
예시

$\sum_{i=3}^{6}i ^{2} = 3 ^{2} + 4 ^{2} + 5 ^{2} + 6 ^{2} = 86$
만약 index 와 하계, 상계를 일일이 표기하지 않아도 될 정도로 맥락이 명확하다면 다음과 같이 생략을 하기도 한다.

$\sum a_i ^{2} = \sum_{i=1}^{n}a ^{2}_i$

임의의 논리 조건이 필요하다면 Summation 의 표기법을 일반화시켜서 조건을 충족하는 모든 수열의 덧셈을 표현할 수도 있다.
예시

다음은 특정 범위 내의 $k$ 에 대한 $f(k)$ 의 덧셈을 표현한다.

$\sum_{0 \leq k < 100}^{}f(k)$

다음은 집합 $S$ 의 원소 $x$ 에 대한 $f(x)$ 의 덧셈을 표현한다.

$\sum_{x \in S}^{}f(k)$
Summation 의 index 를 다음과 같이 일반화할 수도 있다.

$\sum_{i}^{}\sum_{j}^{} = \sum_{i,j}^{}$

이러한 표기법들은 $\displaystyle \prod_{}^{}$ 에서도 통용된다.

Properties of Summation✔

Distributivity (1)

\sum_{n=s}^kC \cdot f(n) = C \cdot \sum_{n=s}^kf(n)

증명

Commutativity and Associativity (1)

\sum_{n=s}^kf(n) \pm \sum_{n=s}^kg(n) = \sum_{n=s}^k(f(n) \pm g(n))

증명

Commutativity and Associativity (2)

\sum_{i=k_0}^{k_1}\sum_{j=l_0}^{l_1}a _{ij} = \sum_{j=l_0}^{l_1}\sum_{i=k_0}^{k_1}a _{ij}

증명

Commutativity and Associativity (3)

\sum_{k \leq j \leq i \leq n}^{} a _{ij} = \sum_{i=k}^{n}\sum_{j=k}^{i}a _{ij}= \sum_{j=k}^{n}\sum_{i=j}^{n}a _{ij}= \sum_{j=0}^{n-k}\sum_{i=k}^{n-j}a _{i+j, i}

증명

Distributivity (2)

\bigg (\sum_{i=0}^{n}a_i \bigg ) \bigg (\sum_{j=0}^{n}b_j \bigg ) = \sum_{i=0}^{n}\sum_{j=0}^{n}a_ib_j

증명

Distributivity (3)

\bigg (\sum_{i=s}^{m}a_i \bigg ) \bigg (\sum_{j=t}^{n}b_j \bigg ) = \sum_{i=s}^{m}\sum_{j=t}^{n}a_ib_j

증명

Powers and logarithm of arithmetic progression✔

등차수열의 합(Sum of arithmetic progression)

자연수 $i, n \in \N$ 에 대하여 다음이 성립한다.

\sum_{i=0}^{n}i = \sum_{i=1}^{n}i = \frac{n(n+1)}{2}

증명

홀수의 합(Sum of odd natural numbers)

자연수 $i, n \in \N$ 에 대하여 다음이 성립한다.

\sum_{i=1}^{n}(2i - 1) = n ^{2}

증명

짝수의 합(Sum of even natural numbers)

자연수 $i, n \in \N$ 에 대하여 다음이 성립한다.

\sum_{i=1}^{n}2i = n(n + 1)

증명

제곱수의 합(Sum of squares)

자연수 $i, n \in \N$ 에 대하여 다음이 성립한다.

\sum_{i=0}^{n}i ^{2} = \sum_{i=1}^{n}i ^{2} = \frac{n(n+1)(2n+1)}{6} = \dfrac{n ^{3}}{3} + \frac{n ^{2}}{2} = \frac{n}{6}

증명

Nicomachus's theorem

자연수 $i, n \in \N$ 에 대하여 다음이 성립한다.

\sum_{i=0}^{n}i ^{3} = \bigg (\sum_{i=0}^{n}i \bigg ) ^{2} = \bigg (\frac{n(n+1)}{2} \bigg ) ^{2} = \dfrac{n ^{4}}{4} + \dfrac{n ^{3}}{2} + \frac{n ^{2}}{4}

증명

Faulhaber's formula

$p > 1$ 와 Bernoulli number $B_k$ 와 binomial coefficient $\displaystyle \binom{p}{k}$ 에 대하여 다음이 성립한다.

\sum_{k=1}^{n}k ^{p} = \dfrac{n ^{p+1}}{p + 1} + \frac{1}{2}n ^{p} + \sum_{k=2}^{p}\binom{p}{k}\dfrac{B_k}{p - k + 1}n ^{p - k + 1}

증명

Summation index in exponents✔

등비수열의 합(sum of a geometric progression) (1)

자연수 $i, n \in \N$ 에 대하여 다음이 성립한다.

\sum_{i=0}^{n-1}a ^{i} = \dfrac{1 - a ^{n}}{1 - a}

증명

등비수열의 합(sum of a geometric progression) (2)

자연수 $i, n \in \N$ 에 대하여 다음이 성립한다.

\sum_{i=0}^{n-1}ia ^{i} = \dfrac{a - na ^{n} + (n - 1)a ^{n+1}}{(1 - a) ^{2}}

증명

산술기하수열의 합(sum of an arithmetico-geometric sequence)

\begin{align}\begin{split} \sum_{i=0}^{n-1}(b + id)a ^{i} &= b \sum_{i=0}^{n-1}a ^{i} + d \sum_{i=0}^{n-1}ia ^{i} \\ &= b \bigg ( \dfrac{1 - a ^{n}}{1 - a} \bigg ) + d \bigg (\dfrac{a - na ^{n} + (n-1)a ^{n+1}}{(1 - a) ^{2}} \bigg ) \\ &= \dfrac{b(1-a ^{n}) - (n-1)da ^{n}}{1 - a} + \dfrac{da(1 - a ^{n-1})}{(1 - a) ^{2}} \\ \end{split}\end{align} \tag*{}

증명

Multiplication✔

곱셈(Multiplication)

덧셈의 반복이다.

곱셈은 덧셈 $+$ 이 정의된 수학적 대상에 대하여 덧셈을 반복하는 것이다. 가령 다음과 같이 $3 \times 4$ 는 $4$ 를 $3$ 번 더한 것이다.

$3 \times 4 = 4 + 4 + 4 = 12$
곱셈(Multiplication) 의 결과를 product 라 한다.

수열의 곱셈(Product of a sequence)

수열 $x_i$ 의 곱셈은 다음과 같이 정의된다.

\prod_{i=m}^{n}x_i = x_m \cdot x _{m+1} \cdot x _{m+2} \cdot \dots \cdot x _{n-1} \cdot x_n

수열은 숫자, 함수, 벡터, 행렬, 다항식 등 임의의 타입의 수학적 대상들로 구성 될 수 있다.
예시

$\prod_{i=1}^{4} i = 24$

Properties of Multiplication✔

Properties of Multiplication

실수체 또는 복소수체에서 곱셈에 대하여 다음이 성립한다.

$x \cdot y = y \cdot x$ (Commutative property)
$(x \cdot y) \cdot z = x \cdot (y \cdot z)$ (Associative property)
$x \cdot (y + z) = x \cdot y + x \cdot z$ (Distributive property)
$x \cdot 1 = x$ (Identity property)
$x \cdot 0 = 0$ (Zero property)
$(-x) + x = 0$ 인 $-x$ 에 대하여 $(-1) \cdot x = (-x)$ 이다. 또한 $(-1) \cdot (-1) = 1$ 이다. (Negation)
$0$ 이 아닌 $x$ 에 대하여 $x \cdot \bigg (\dfrac{1}{x} \bigg ) = 1$ 인 $\dfrac{1}{x}$ 가 존재한다. (Inverse element)

Associativity and Commutativity (1)

\prod_{i=1}^{n}x_iy_i = \bigg (\prod_{i=1}^{n}x_i \bigg )\bigg (\prod_{i=1}^{n}y_i \bigg )

증명

Associativity and Commutativity (2)

\bigg (\prod_{i=1}^{n}x_i \bigg ) ^{a} = \prod_{i=1}^{n}x_i ^{a}

증명

a \in \N, x_i \in \R _{>0} : \prod_{i=1}^{n}x ^{a_i} = x ^{\sum_{i=1}^{n}a_i}

증명

Exponentiation✔

Integer Exponent✔

정수 제곱(integer exponent)

$a \in \R, n \in \Bbb{Z}_{>0}$ 에 대하여 $a$ 의 $n$ 제곱을 다음과 같이 정의한다.

a ^{n} = \overbrace{a \times a \times \dots \times a}^{n}

Rational Exponent✔

유리수 제곱(rational exponent)

$m,n \in \Bbb{Z}, n > 0, \gcd (m, n) = 1$ 인 $m, n$ 에 대하여 다음과 같이 정의한다.

$n$ 이 홀수면 $a \in \R$ 에 대하여 $a ^{m/n} = \sqrt[n]{a ^{m}}$ 로 정의한다.
$n$ 이 짝수면 $a \in \R _{\geq 0}$ 에 대하여 $a ^{m/n} = \sqrt[n]{a ^{m}}$ 로 정의한다.

$n$ 이 짝수일 경우 음의 실수를 밑으로 가지는 유리수 제곱은 정의하지 않는다. 왜냐하면 그 값이 복소수가 되기 때문이다. 가령 $\sqrt[]{-1} = i$ 가 된다.

Natural Exponential Function✔

자연지수함수(natural exponential function)

자연지수함수 $\exp:\R \to \R$ 를 다음과 같이 정의한다.

\exp (x) = \sum_{n=0}^{\infty}\dfrac{x ^{n}}{n!} = 1 + x + \dfrac{x ^{2}}{2!} + \dfrac{x ^{3}}{3!} + \dots

이항정리에 의하여 이 무한급수는 다음과 같다.

$\exp (x) = \lim_{n \to \infty} \left( 1 + \frac{x}{n} \right) ^{n}$

자연지수함수의 성질 (1)

자연지수함수 $\exp (x)$ 에 대하여 다음이 성립한다.

$\exp (x)$ 가 모든 $x \in \R$ 에 대하여 절대수렴한다.
$\exp (x)$ 가 $\R$ 에서 미분가능하고, $\exp '(x) = \exp (x)$ 이다.
$\forall x, y \in \R : \exp (x + y) = \exp (x)\exp (y)$
$\exp (0) = 1, \exp (-x) = \dfrac{1}{\exp (x)}$
$\forall x \in \R : \exp (x) > 0$

이 정리에 의하여 $\exp (x)$ 가 실질적으로 지수함수의 모든 기능을 한다는 것이 증명되었다.
증명

오일러의 수(Euler's number)

자연지수함수 $\exp (x)$ 에 대하여 $e = \exp (1)$ 라고 정의한다.

다음과 같이 정의된 것과 동치이다.

$\lim_{n \to \infty } \left( 1 + \frac{1}{n} \right) ^{n} = e$

$t = \dfrac{1}{n}$ 로 두면 $x \to \infty \implies t \to 0$ 이므로 다음과 같이 정의할 수 있다.

$\lim_{t \to 0} (1 + t)^{1/t} = e$
$e$ 는 다음과 같은 값을 갖는다.

$e = 2.718281 \dots$

자연지수함수의 성질 (2)

자연지수함수 $\exp (x)$ 에 대하여 다음이 성립한다.

$\forall m, n \in \Bbb{Z} : \exp \left( \frac{m}{n} \right) = (\sqrt[n]{e})^{m}$
$\displaystyle \forall n \in \N : \lim_{x \to \infty} x ^{n}e ^{-x} = 0$
$e ^{x}$ 가 다음을 만족하는 역함수 $\ln x:\R _{>0} \to \R$ 를 가진다.

$(\forall y \in \R : \ln e ^{y} = y) \land (\forall x > 0 : e ^{\ln x} = x)$
$(\ln x)' = \dfrac{1}{x}$
$x,y > 0 : \ln xy = \ln x + \ln y$
$n \in \N, t > 0 : t ^{n} = e ^{n \ln t}$
$x \in \R, t > 0 : t ^{x} = e ^{x \ln t}$

1) 에 의하여 $\exp (x)$ 를 $e$ 를 $x$ 만큼 거듭제곱한 것으로 볼 수 있다.

7) 로 실수 지수 함수를 정의할 수 있다.
증명

Real Exponent✔

정의 8.4.2 실수 제곱(real exponent)

$a \in \R _{>0}, x \in \R$ 에 대하여 실수 제곱을 다음과 같이 정의한다.

a ^{x} = e ^{x \ln a}

이 정의에 의하여 $3^{\pi }$ 같은 제곱도 정의할 수 있다.
코시 수열을 통하여 유리수로 실수를 얻어내는 다음과 같은 방식으로도 실수 제곱을 정의할 수 있다.

$a \in \R _{>0}, x \in \R, r \in \Bbb{Q} : a ^{x} = \lim_{r \to x} a ^{r}$

가령 $3 ^{\pi }$ 를 다음과 같이 정의된 모든 축소구간열에 포함되는 원소로 정의한다.

$[3 ^{3}, 3 ^{4}], [3 ^{3.1}, 3 ^{3.2}], [3 ^{3.14}, 3 ^{3.15}], [3 ^{3.141}, 3 ^{3.142}], \dots$

축소구간성질에 의하여 극한 구간의 길이는 $0$ 이고, 이 축소구간열들은 하나의 공통된 원소를 가지며, 이 원소를 $3 ^{\pi }$ 로 정의하는 것이다.

Complex Exponents✔

복소수 제곱(complex exponents)

$a \in \R _{>0}, z \in \Bbb{C}$ 에 대하여 복소수 제곱을 다음과 같이 정의한다.

a ^{z} = e ^{z \ln a}

복소수 제곱은 자연 지수 함수에 의하여 정의된 실수 제곱을 단지 복소수로 바꾸어 정의한 것이다.
오일러 공식에 의하여 다음이 성립한다.

$a ^{x + iy} = a ^{x}(\cos (y \ln a) + i \sin (y \ln a))$

Euler's Formula✔

오일러 공식(euler's formula)

$x \in \R$ 에 대하여 다음이 성립한다.

e ^{ix} = \cos x + i \sin x

증명

자연지수함수의 정의와 사인/코사인 함수의 멱급수 전개에 의하여 이 증명이 성립한다.

복소수 $z = r(\cos \theta + i \sin \theta)$ 에 대하여 다음이 성립한다.

z = r e ^{i \theta}

증명

복소수의 극형식과 오일러 공식에 의하여 증명된다. ■

Most Beautiful Theorem in Mathematics✔

오일러 항등식(Euler's identity)

e ^{i \pi } = - 1

수학에서 가장 아름다운 정리라고 알려져있다.

$\pi \approx 3.14$ 이고 $e \approx 2.71$ 이므로, 러프하게 $3.14$ 에 허수 $i$ 를 곱한 것을 $2.71$ 에 제곱하면 $-1$ 이 나온다는 것이다.
다음과 같이 쓰면 수학의 최중요 다섯 원소 $e, i, \pi , 0, 1$ 와 수학의 근본 기호 $+, =$ 이 가장 아름답고 간결한 형태로 나타난다고 하여 이 형태로도 많이 쓴다.

$e ^{i \pi } + 1 = 0$
증명

오일러 공식에 $x = \pi$ 를 대입하면 바로 나온다. ■

Trigonometry✔

Radian✔

라디안(호도법, radian)

주어진 각에 대하여 각의 꼭짓점을 중심으로 하고 반지름 $r > 0$ 을 갖는 원 $O$ 를 취하자. $O$ 에서 주어진 각에 대한 호의 길이 $l$ 에 대하여 다음과 같은 $l$ 과 $r$ 의 비를 각의 라디안 값으로 정의한다.

\frac{l}{r}

주의해야 할 점은 $x$ 축으로부터 시계방향으로 라디안을 측정하면 음수이고, 반시계방향으로 라디안을 구하면 양수로 정의한다는 것이다.
$l/r$ 은 원의 선택과 관계없이 주어진 각을 특정할 수 있기 때문에 이 값으로 각을 잘 정의 수 있다.
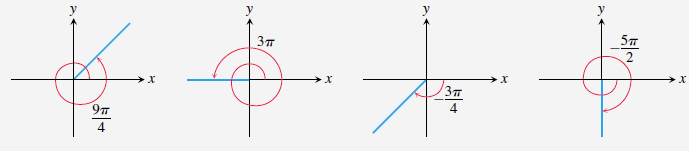
라디안의 장점은 길이와 길이의 비율로 정의되어 길이라는 단위가 사라져서 무차원 단위가 된다는 것이다. 즉, 라디안은 단위를 생략할 수 있는 순수한 수이다. 따라서 수학에서 각을 표현할 때 라디안을 널리 사용한다.
예시

$180 \degree$ 는 길이가 $\pi r$ 인 호를 대하므로 $\pi$ 라디안이다.

Trigonometric Ratio✔

밑변(adjacent), 높이(opposite), 빗변(hypotenuse)

직각삼각형의 직각이 아닌 각 $\theta$ 에 대하여 다음과 같이 정의한다.

$\theta$ 로부터 직각으로 향하는 선분을 밑변이라 한다.
$\theta$ 로부터 직각으로 향하지 않는 선분을 빗변이라 한다.
$\theta$ 와 마주보는 선분을 높이라 한다.

다음 그림은 직각삼각형의 밑변, 빗변, 높이를 보여준다.

삼각비(trigonometric ratio)

삼각비는 직각삼각형의 두 변의 길이의 비율로써 직각삼각형의 직각이 아닌 각 $\theta$ 에 대한 빗변 $h$ , 밑변 $b$ , 높이 $a$ 에 대하여 다음과 같이 정의한다.

빗변에 대한 높이의 비율을 사인(sine) $\sin \theta = \dfrac{a}{h}$ 이라 한다.
빗변에 대한 밑변의 비율을 코사인(cosine) $\cos \theta = \dfrac{b}{h}$ 이라 한다.
밑변에 대한 높이의 비율을 탄젠트(tangent) $\tan \theta = \dfrac{a}{b}$ 이라 한다.
높이에 대한 빗변의 비율을 코시컨트(cosecant) $\csc \theta = \dfrac{h}{a}$ 이라 한다.
밑변에 대한 빗변의 비율을 시컨트(secant) $\sec \theta = \dfrac{h}{b}$ 이라 한다.
높이에 대한 밑변의 비율을 코탄젠트(cotangent) $\cot \theta = \dfrac{b}{a}$ 이라 한다.

삼각법은 이를 통하여 각도만으로 변의 길이를 비교 할 수 있었기에 고대로부터 개발되었다.
삼각비의 정의역은 $0 \degree < x < 90 \degree$ 이다.

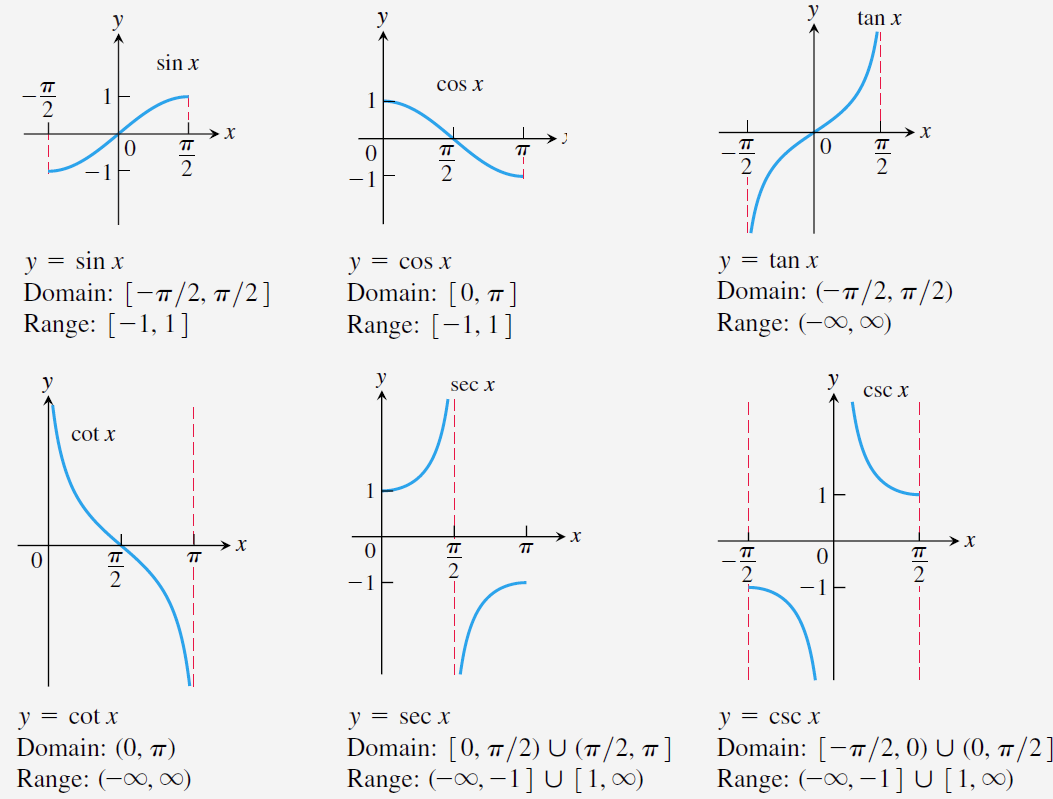
Trigonometric Functions✔

삼각함수(trigonometric functions)

$\R$ 에서 정의된 삼각함수는 단위원 $x ^{2} + y ^{2} = 1$ 의 좌표 $P(x, y)$ 에 대하여 주어진 라디안 각 $\theta$ 을 삼각비로 나타내는 함수로써 다음과 같이 정의된다.

사인함수를 $\sin \theta = y$ 로 정의한다.
코사인함수를 $\cos \theta = x$ 로 정의한다.
탄젠트함수를 $\tan \theta = \dfrac{y}{x} = \dfrac{\sin \theta}{\cos \theta}$ 로 정의한다.
코시컨트함수를 $\csc \theta = \dfrac{1}{y} = \dfrac{1}{\sin \theta}$ 로 정의한다.
시컨트함수를 $\sec \theta = \dfrac{1}{x} = \dfrac{1}{\cos \theta}$ 로 정의한다.
코탄젠트함수를 $\cot \theta = \dfrac{x}{y} = \dfrac{\cos \theta}{\sin \theta}$ 로 정의한다.

다음 표는 삼각함수의 정의역과 치역을 보여준다.
다음 그림은 단위원의 좌표 $P(x, y)$ 와 반지름 $r = 1$ 과 주어진 라디안 각 $\theta$ 를 보여준다. 위 정의는

$\sin \theta = \dfrac{y}{r} = y, \enspace \cos \theta = \dfrac{x}{r} = x, \enspace \csc \theta = \dfrac{r}{y} = \dfrac{1}{y}, \enspace \sec \theta = \dfrac{r}{x} = \dfrac{1}{x}$

와 같이 유도된다.
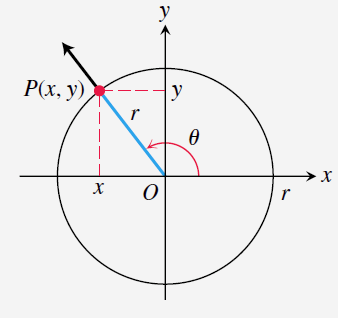
다음 그림은 $\sin \theta = y$ 와 $\cos \theta = x$ 와 $\tan \theta = \dfrac{y}{x}$ 의 그래프를 보여준다.
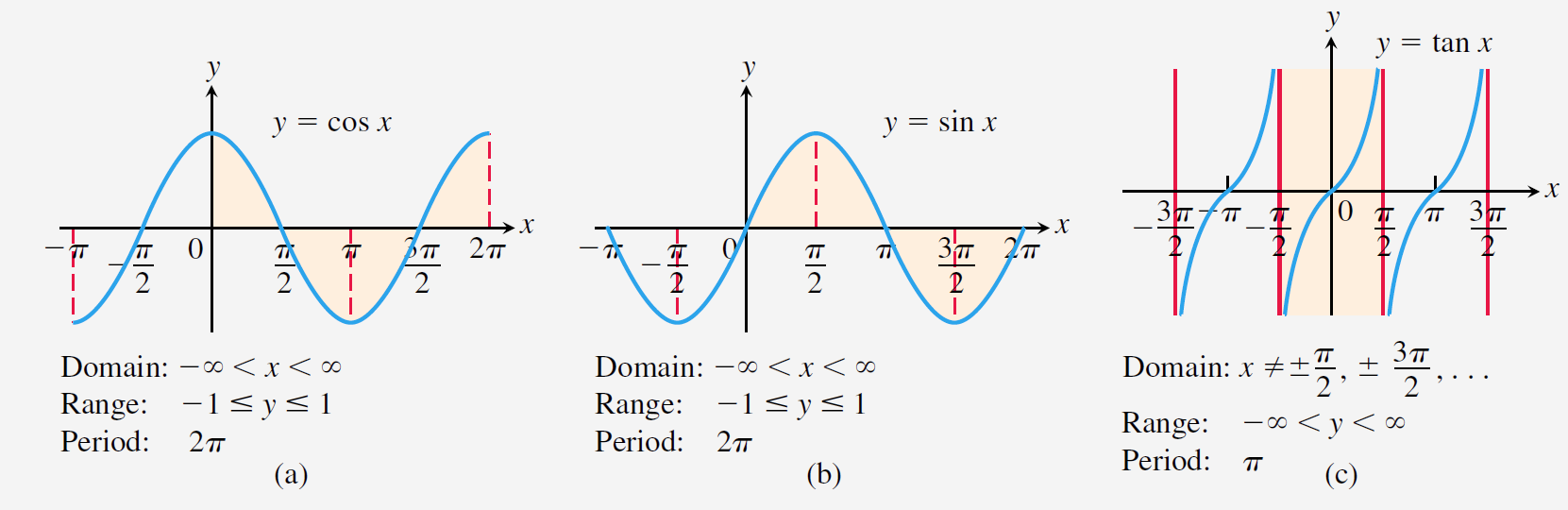
다음 그림은 $\sec \theta = \dfrac{1}{x}$ 와 $\csc \theta = \dfrac{1}{y}$ 와 $\cot \theta = \dfrac{x}{y}$ 의 그래프를 보여준다.

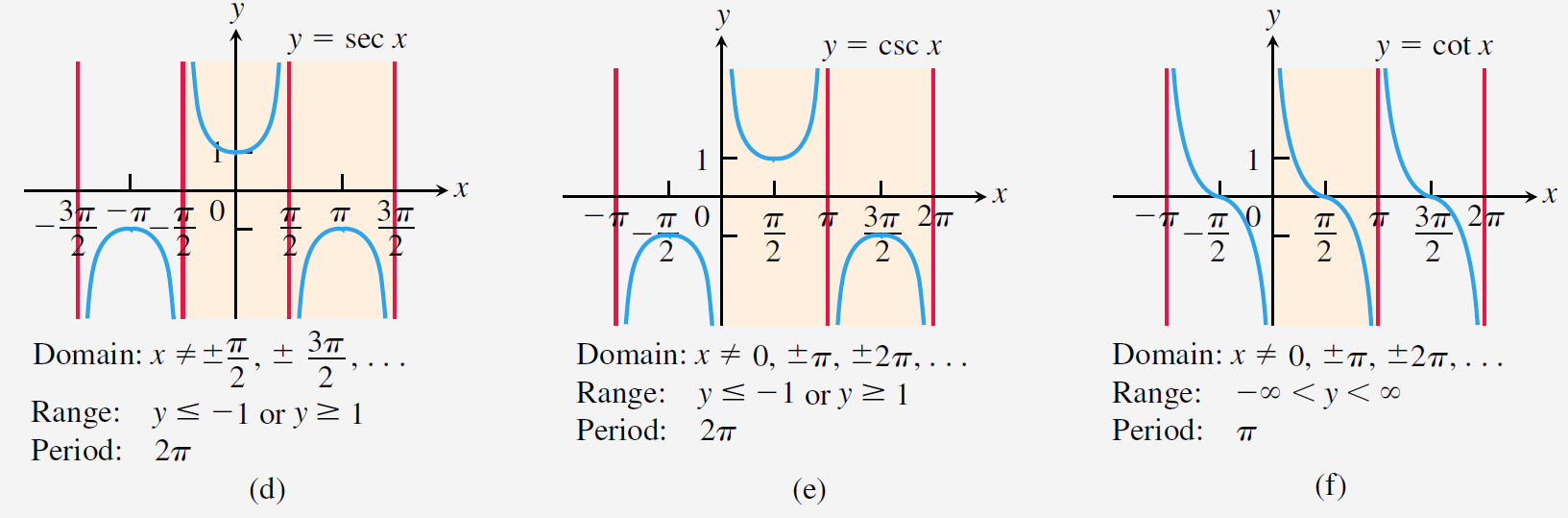
코시컨트 함수 $\csc \theta = \dfrac{1}{y}$ 그래프는 다음과 같이 그려진다.

삼각함수의 특수각

직각삼각형의 성질에 의하여 특정한 각에서 삼각함수의 정확한 값을 알 수 있다.

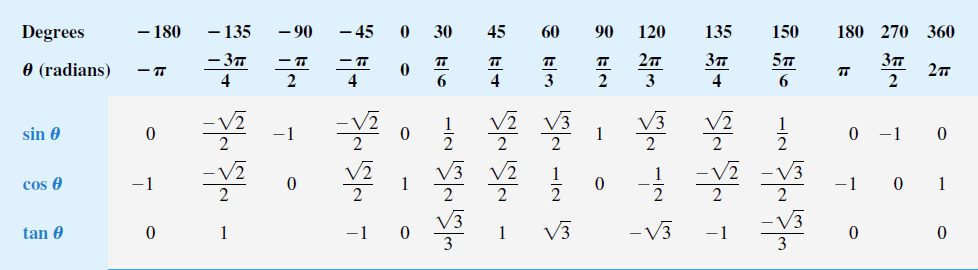
탄젠트 함수 $\tan \theta = \dfrac{y}{x}$ 는 분모 $x$ 가 $0$ 이 되는 지점인 $90 \degree = \dfrac{\pi }{2}$ 와 $-90 \degree = -\dfrac{\pi }{2}$ 에서 값이 정의되지 않는다.
증명

피타고라스의 정리에 의하여 직각삼각형이 다음과 같은 특정한 각을 이루면 변들이 특수한 비율을 갖는다.

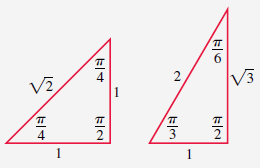
나머지 값들은 삼각함수의 정의에 의하여 자명하다. ■

Properties of Trigonometric Functions✔

주기함수(periodic function)

함수 $f(x)$ 가 $p > 0$ 에 대하여 $f(x + p) = f(x)$ 이면 주기 $p$ 를 갖는 주기함수라 한다.

삼각함수의 주기(periods of trigonometric functions)

$\tan (x), \cot (x)$ 는 주기 $\pi$ 를 갖는 주기함수이고, $\sin (x), \cos (x), \sec (x), \csc (x)$ 는 주기 $2 \pi$ 를 갖는 주기함수이다. 즉, 다음이 성립한다.

\tan (x + \pi ) = \tan x, \qquad \cot (x + \pi ) = \cot x

\sin (x + 2\pi ) = \sin x, \qquad \cos (x + 2\pi ) = \cos x

\sec (x + 2\pi ) = \sec x, \qquad \csc (x + 2\pi ) = \csc x

증명

삼각함수 그래프를 적절히 이동시켜보면 바로 알 수 있다. ■

Even/Odd Function✔

홀함수(기함수, odd function), 짝함수(우함수, even function)

함수 $f: D \to \R$ 의 정의역 $D \subset \R$ 이 $-D = D$ 인 구간일 때 다음과 같이 정의한다.

$\forall x \in D : f(-x) = -f(x)$ 이면 $f$ 를 홀함수라 한다.
$\forall x \in D : f(-x) = f(x)$ 이면 $f$ 를 짝함수라 한다.

홀함수는 원점에 대한 대칭 함수이고, 짝함수는 $y$ 축 대칭 함수이다.
예시

삼각함수의 홀짝성

삼각함수의 홀짝성은 다음과 같다.

$\cos x, \sec x$ 는 짝함수이다.

$\cos (-x) = \cos x, \qquad \sec (-x) = \sec x$
$\sin x, \tan x, \csc x, \cot x$ 는 홀함수이다.

$\sin (-x) = - \sin x, \qquad \tan (-x) = - \tan x$

$\csc (-x) = - \csc x, \qquad \cot (-x) = - \cot x$

증명

삼각함수 그래프를 적절히 원점, 또는 $y$ 축에 대하여 대칭시켜보면 바로 알 수 있다. ■

삼각함수의 대칭

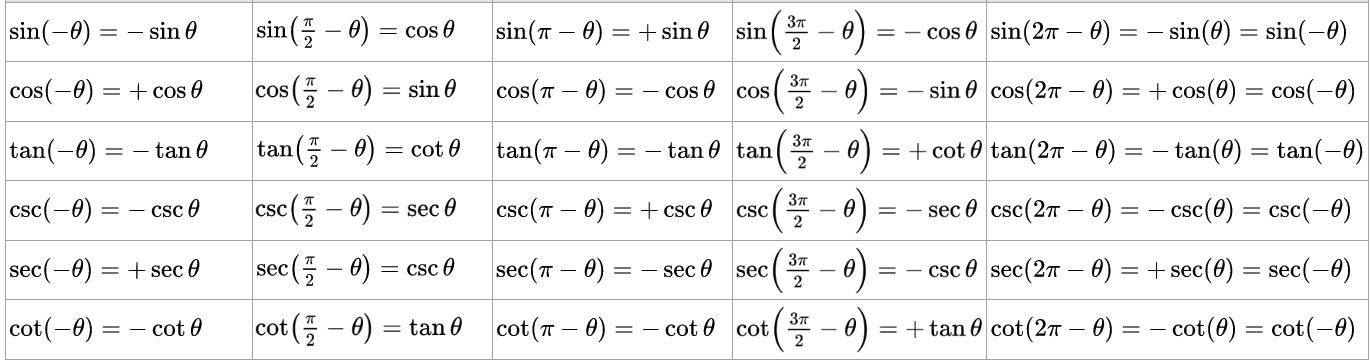
증명

삼각함수의 그래프를 보면서 적절히 $y$ 축 대칭, 원점 대칭을 시행하고 $k \pi$ 만큼 이동시켜보면 바로 알 수 있다. ■

삼각함수의 주기성

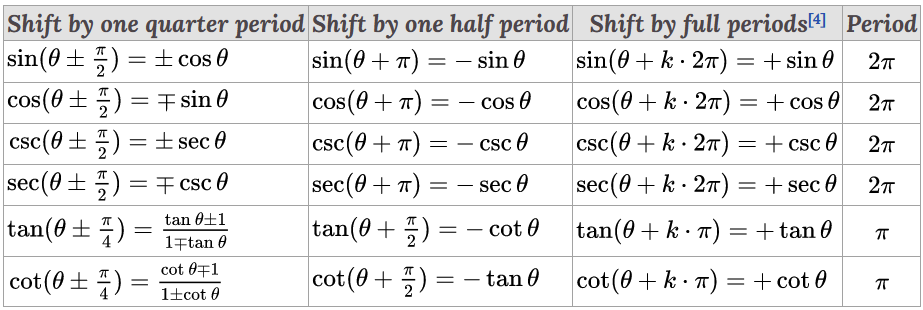
증명

삼각함수 그래프를 적절히 이동시켜보면 바로 알 수 있다. ■

Theorem of Trigonometric Functions✔

Trigonometric Identities

삼각함수에 대하여 다음이 성립한다.

$\cos ^{2}\theta + \sin ^2 \theta = 1$
$1 + \tan ^{2}\theta = \sec ^2 \theta$
$1 + \cot ^{2}\theta = \csc ^2 \theta$

증명

1:

$\sin \theta = y, \cos \theta = x$ 을 단위원의 방정식 $x^2 + y^2 = 1$ 에 대입하면 바로 나온다. ■

2, 3:

1) 에 $\cos ^2 \theta$ 를 나누면 2) 를 얻고 $\sin ^2 \theta$ 를 나누면 3) 을 얻는다. ■

삼각함수의 덧셈정리(Addition Formulas)

삼각함수에 대하여 다음이 성립한다.

$\sin(x +y) = \sin x \cos y + \cos x \sin y$
$\sin (x - y ) = \sin x \cos y - \cos x \sin y$
$\cos (x + y) = \cos x \cos y - \sin x \sin y$
$\cos (x - y ) = \cos x \cos y + \sin x \sin y$
$\tan (x + y) = \dfrac{\tan x + \tan y }{1 - \tan x \tan y }$
$\tan (x - y) = \dfrac{\tan x - \tan y }{1 + \tan x \tan y }$

증명

1, 2, 3, 4:

오일러 공식에 의하여 다음이 성립한다.

$\begin{align}\begin{split} \cos (x + y) + i \sin (x + y)&= e ^{i(x + y)} = e ^{ix}e ^{iy}\\ &= (\cos x + i \sin x)(\cos y + i \sin y) \\ &= (\cos x \cos y - \sin x \sin y) + i(\sin x \cos y + \cos x \sin y) \end{split}\end{align} \tag*{}$

이 결과의 허수부에 의하여 1) 이 증명되고, 실수부에 의하여 3) 이 증명된다. 2) 는 1) 에 $\sin (-x) = - \sin x$ 를 적용하여 얻고, 4) 는 3) 에 $\cos (-x) = \cos x$ 를 적용하여 얻는다. ■

5, 6:

5) 는 이 증명에 의하여 증명되고, 6) 은 $\tan (-x) = - \tan x$ 를 적용하여 얻는다. ■

배각의 공식(Double-Angle Formulas)

삼각함수에 대하여 다음이 성립한다.

$\sin 2x = 2 \sin x \cos x$
$\cos 2x = \cos ^2 x - \sin ^2x$
$\tan 2x = \dfrac{2 \tan x}{1 - \tan ^2x}$

증명

1:

사인함수의 덧셈정리 $\sin(x +y) = \sin x \cos y + \cos x \sin y$ 에 $x = y$ 로 두면 다음이 성립한다.

$\sin 2 x = 2 \sin x \cos x \tag*{■}$

2:

코사인함수 덧셈정리 $\cos (x + y) = \cos x \cos y - \sin x \sin y$ 에 $x = y$ 로 두면 다음이 성립한다.

$\cos 2 x = \cos ^{2}x - \sin ^{2} x \tag*{■}$

3:

탄젠트함수 덧셈정리 $\tan (x + y) = \dfrac{\tan x + \tan y }{1 - \tan x \tan y }$ 에 $x = y$ 로 두면 다음이 성립한다.

$\tan 2x = \frac{2\tan x}{1 - \tan ^{2} x} \tag*{■}$

반각의 공식(Half-Angle Formulas)

삼각함수에 대하여 다음이 성립한다.

$\sin ^{2} \dfrac{a }{2} = \dfrac{1 - \cos a }{2}$
$\cos ^{2}\dfrac{a }{2} = \dfrac{1+\cos a }{2}$
$\tan ^{2} \dfrac{a }{2} = \dfrac{1-\cos a }{1+\cos a }$

증명

1:

배각의 공식으로부터 $\cos 2 a = 1 - 2 \sin ^{2} a$ 를 얻고, 곧 다음이 성립한다.

$\sin ^{2} a = \dfrac{1 - \cos 2 a }{2}$

$a$ 대신 $\dfrac{a }{2}$ 를 대입하면 정리가 나온다. ■

2:

배각의 공식으로부터 $\cos 2 a = 2 \cos ^{2} a -1$ 를 얻고, 곧 다음이 성립한다.

$\cos ^{2} a = \dfrac{1 + \cos 2 a}{2}$

$a$ 대신 $\dfrac{a }{2}$ 를 대입하면 정리가 나온다. ■

3:

탄젠트는 코사인 값에 대한 사인 값의 비이므로 다음이 성립한다.

$\tan ^{2} \dfrac{a }{2} = \dfrac{\sin ^{2} \dfrac{a }{2}}{\cos ^{2} \dfrac{a }{2}} = \dfrac{\dfrac{1-\cos a }{2}}{\dfrac{1+\cos a }{2}} = \dfrac{1-\cos a }{1+\cos a } \tag*{■}$

코사인 법칙(Law of Cosines)

삼각형 $ABC$ 에 대하여 $A$ 를 마주보는 변 $a$ , $B$ 를 마주보는 변 $b$ , $C$ 를 마주보는 변 $c$ 에 대하여 다음이 성립한다.

$a^2 = b^2 + c^2 -2bc \cos A$
$b^2 = c^2 + a^2 -2ca \cos B$
$c^2 = a^2 + b^2 -2ab \cos C$

증명

3:

다음 그림처럼 삼각형 $ABC$ 의 세 점 $A, B, C$ 의 각을 각각 $\alpha , \beta , \gamma$ 로 두고 마주하는 변을 각각 $a, b, c$ 로 잡자.

다음 그림은 코사인의 정의에 의하여 $c = a \cos \beta + b \cos \alpha$ 가 성립함을 보여준다.

같은 원리로 다음을 얻는다.

$a = c \cos \beta + b \cos \gamma$

$b = c \cos \alpha + a \cos \gamma$

이를 기반으로 다음이 성립한다.

$a ^{2} = ac \cos \beta + ab \cos \gamma \tag{1}$

$b ^{2} = bc \cos \alpha + ab \cos \gamma \tag{2}$

$c ^{2} = ac \cos \beta + bc \cos \alpha \tag{3}$

$(1)$ 과 $(2)$ 를 더하고 $(3)$ 을 빼면 다음이 성립한다.

$a ^{2} + b ^{2} - c ^{2} = 2ab \cos \gamma$

이것을 다음과 같이 정리하여 코사인 법칙을 얻는다.

$\therefore c ^{2} = a ^{2} + b ^{2} -2ab \cos C \tag*{■}$

1, 2:

3) 을 증명했듯이 1), 2)도 같은 논리로 증명할 수 있다. ■

사인법칙(Law of Sines)

삼각형 $ABC$ 와 각 $A, B, C$ 와 각각 마주보는 변 $a, b, c$ 와 삼각형 $ABC$ 의 외접원의 반지름 $R$ 에 대하여 다음이 성립한다.

\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R

증명

https://proofwiki.org/wiki/Law_of_Sines#Proof_1

Inverse Trigonometric Functions✔

삼각함수의 역함수(inverse trigonometric functions)

정의역이 제한되어 전단사 함수가 된 삼각함수의 역함수를 다음과 같이 정의한다.

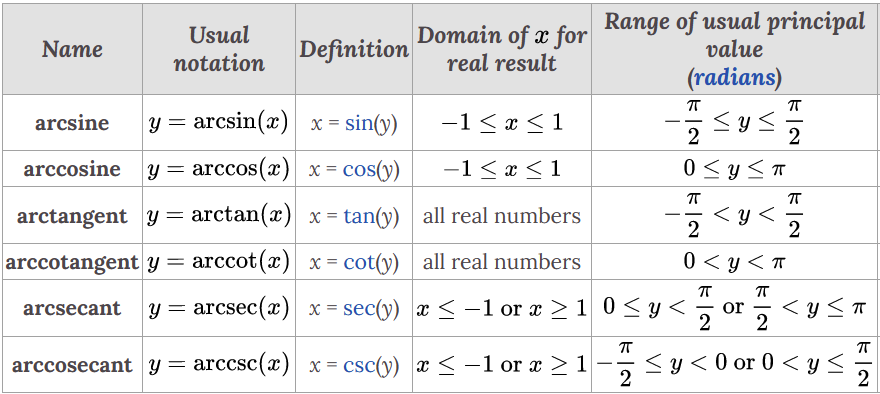
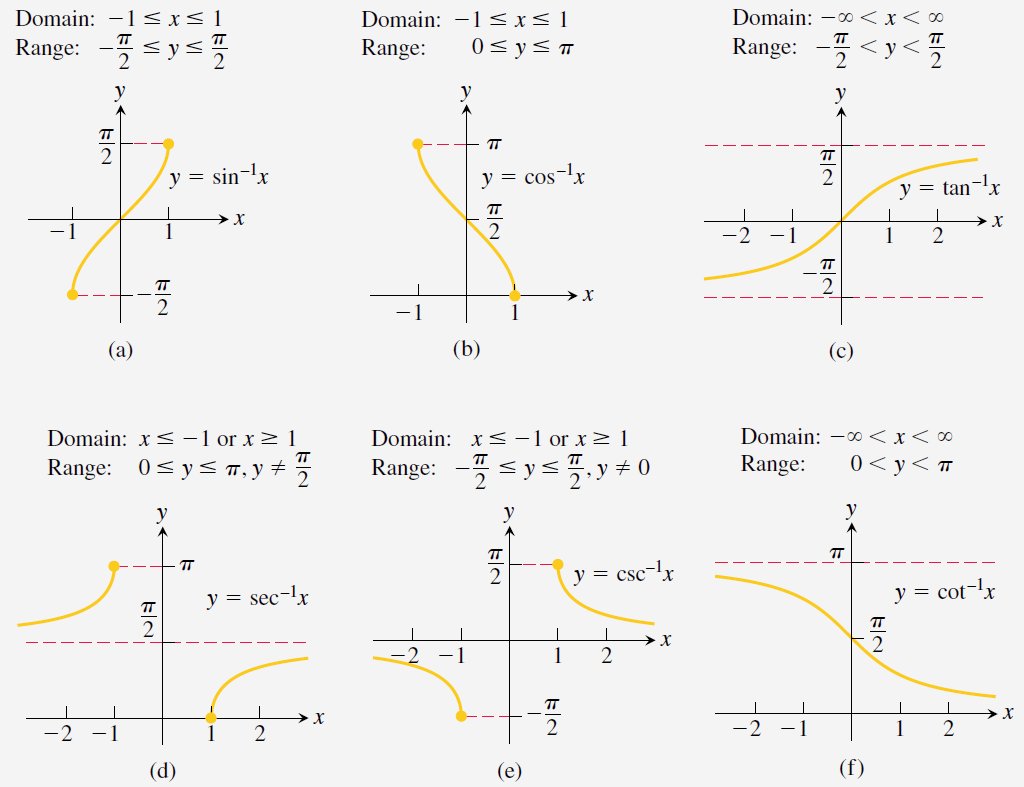
삼각함수는 전단사가 아니므로 역함수를 갖지 않는다. 그러나 다음과 같이 정의역을 제한하면 전단사가 되고, 역함수를 갖게 된다.

이것을 통하여 삼각함수의 역함수가 다음과 같이 정의된다.

Hyperbolic Functions✔

쌍곡선 함수(hyperbolic functions)

쌍곡선 함수를 다음과 같이 정의한다.

Hyperbolic sine: $\sinh x = \dfrac{e^x - e ^{-x}}{2}$
Hyperbolic cosine: $\cosh x = \dfrac{e^x + e ^{-x}}{2}$
Hyperbolic tangent: $\tanh x = \dfrac{\sinh x}{\cosh x} = \dfrac{e^x - e ^{-x}}{e ^{x} + e ^{-x}}$
Hyperbolic cosecant: $\operatorname{csch} x = \dfrac{1}{\sinh x} = \dfrac{2}{e ^{x} - e ^{-x}}$
Hyperbolic secant: $\operatorname{sech} x = \dfrac{1}{\cosh x} = \dfrac{2}{e ^{x} + e ^{-x}}$
Hyperbolic cotangent: $\coth x = \dfrac{\cosh x}{\sinh x} = \dfrac{e^x + e ^{-x}}{e ^{x} - e ^{-x}}$

삼각함수를 단위원으로 정의했듯이, 쌍곡함수는 쌍곡선으로 정의한다. 삼각함수와 쌍곡함수는 매우 유사한 성질을 가지지만, 쌍곡함수는 주기함수가 아니다.

단위원 $x ^{2} + y ^{2} = 1$ 의 좌표를 임의의 실수 $u$ 에 대하여 $(\cos u, \sin u)$ 로 나타낼 수 있고, 곧 다음이 성립한다.

$\sin ^2u + \cos ^2u = 1$

단위 쌍곡선 $x^2 - y^2 = 1$ 의 좌표는 $(\cosh u, \sinh u)$ 로 나타낼 수 있고, 이에 따라 다음이 성립한다.

$\cosh ^2u - \sinh ^2u = 1$
쌍곡함수는 다음과 같은 그래프를 갖는다.

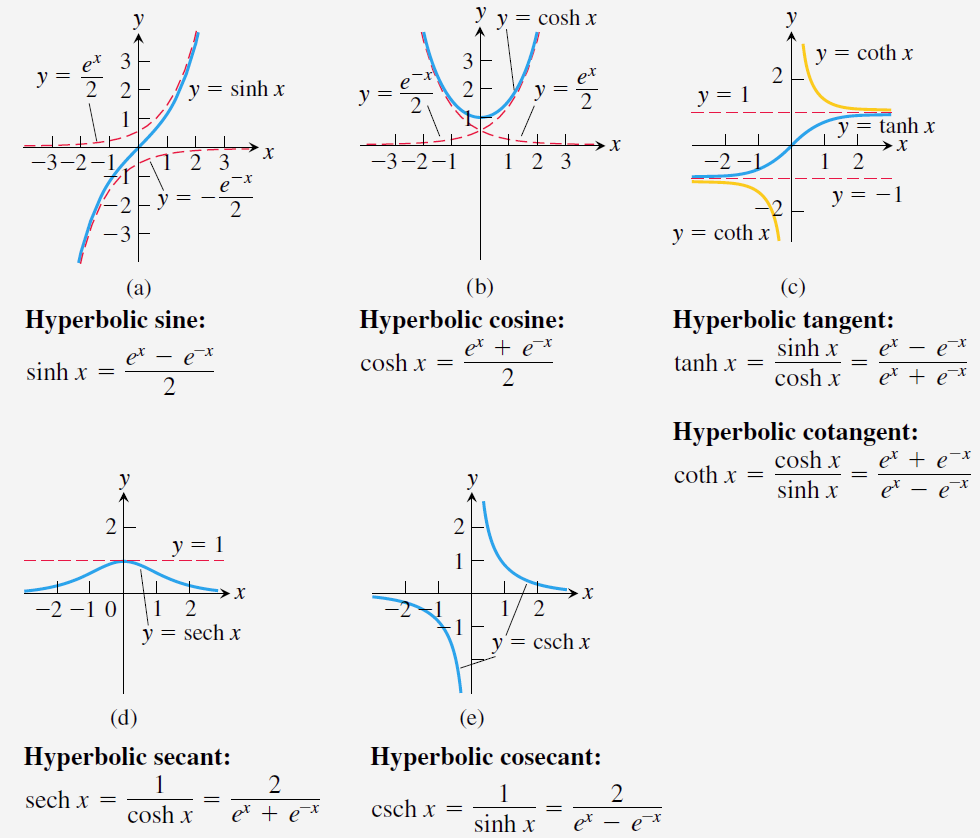
Theorems of hyperbolic functions✔

Identities for hyperbolic functions

쌍곡함수에 대하여 다음이 성립한다.

$\cosh ^2 x - \sinh ^2x = 1$
$\sinh 2x = 2 \sinh x \cosh x$
$\cosh 2x = \cosh ^2x + \sinh ^2x$
$\cosh ^2x = \dfrac{\cosh 2x + 1}{2}$
$\sinh ^2x = \dfrac{\sinh 2x - 1}{2}$
$\tanh ^2x = 1 - \operatorname{sech} ^2x$
$\coth ^2x = 1 + \operatorname{csch} ^2x$

증명

Abbott, S. (2015). Understanding analysis. Springer.

Thomas, G. B., Jr, Weir, M. D., & Hass, J. R. (2014). Thomas’ calculus: Early Transcendentals. Pearson Higher Ed.

Wikipedia contributors. (2024b, June 29). Summation. Wikipedia. https://en.wikipedia.org/wiki/Summation