Determinants
Contents
- Determinants of 2 × 2 Matrix
- Determinants
- Determinants of Identity Matrix
- Properties of Determinant
- Redefining the Determinant
- Determinant and Rank
- Determinant and Elementary Operation
- Determinant of Upper Triangular Matrix
- Determinant of Elementary Matrix
- Determinant of Transpose
- Determinant of Submatrix
- Cramer's Rule
- n-dimensional volume of parallelepiped
- Determinant of Similar Matrices
Determinants of 2 × 2 Matrix✔
Properties of Determinants of 2 × 2 Matrix✔
함수
-
증명
행렬
따라서 다음이 성립한다.
그러므로 함수
정리 4.1
함수
-
이 정리는 함수
-
증명
1:
2:
1) 과 비슷하게 증명된다. ■
정리 4.2
행렬
-
-
-
증명
이는
역으로 다음과 같은 가역행렬
정리 3.4 따름정리 에 의하여 기본연산은 행렬의 랭크를 보존한다. 이는 다음을 뜻한다.
즉,
Area of a parallelogram✔
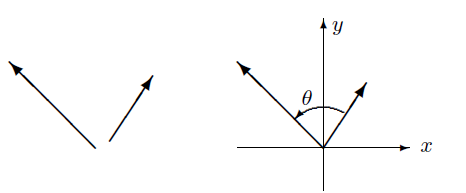
각(angle)
-
예시
다음과 그림에서 왼쪽 두 벡터가 이루는 각은 같은 크기와 방향을 가지고 시점이 원점인 두 벡터가 이루는 각이다.
향(orientation)
-
이 정리와 정리 4.2 에 의하여 위 식의 분모는
-
- 증명
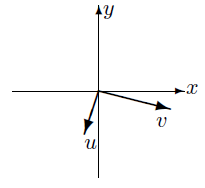
오른손 좌표계(right-handed coordinate system)
-
예시
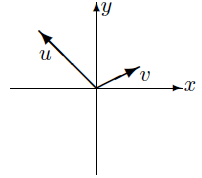
왼손 좌표계(left-handed coordinate system)
-
예시
행렬식
- 증명
문제 4.1-11
함수
-
행렬의 한 행이 고정되어 있을 때, 나머지 행에 대하여
-
행렬
-
함수
-
기본행렬
-
행렬
-
증명
성질 1) 로부터 다음이 성립한다.
이때 성질 1), 2), 3) 으로부터 다음이 성립한다.
또한 성질 1), 2), 3) 으로부터 다음이 성립한다.
그러므로 다음을 얻는다.
그러므로
조건 2) 는
문제 4.1-12
문제 4.1-11 의 함수
-
증명
문제 4.1-11 의 증명에 의하여 증명이 끝난다.
- 증명
평행사변형(parallelogram)
원점을 시점으로 하는 벡터
-
-
예시
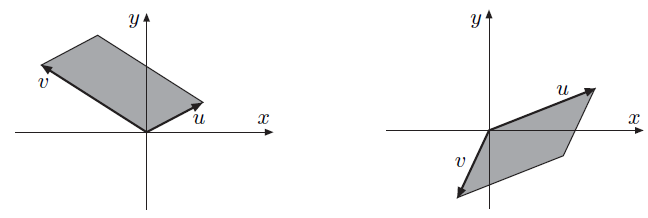
-
예시
-
다음 증명은 이 정리가
-
증명
이때
먼저 벡터
그러므로
이로써
같은 변으로 구성된 평행사변형은 선분이 되어 넓이가
이로써
이제 성질 1) 의 벡터합을 증명하자. 즉
그러므로 성질 2) 에 의하여 다음이 성립한다.
같은 논리로 다음을 증명할 수 있다.
이로써
마지막으로 성질 3) 을 증명하자.
즉,
Determinants✔
소행렬식(minor)
-
예시
여인수(cofactor)
스칼라
여인수 전개(cofactor expansion, 라플라스 전개, Laplace expansion)
- 즉,
행렬식(determinant)
행렬
-
이는 연립 일차 방정식의 풀이를 연구하다가
-
즉,
-
예시
Determinants of Identity Matrix✔
-
증명
■
Properties of Determinant✔
정리 4.3
-
이 정리는 2형 기본행연산과 행렬식 사이의 관계를 말해준다. 즉, 위 정리에서
이는 행렬
-
증명
이는
그러므로
이는
그러므로
정리 4.3 따름정리
행렬
-
증명
스칼라
정리 4.3 보조정리 1
-
행렬식은 정사각행렬의 1행에 대한 여인수 전개로 정의되었지만, 이 정리는 정사각행렬이 특정 조건을 만족할 경우 임의의 행에 대한 여인수 전개로도 행렬식을 구할 수 있다는 것을 말해준다.
-
증명
그러므로
행렬
그러므로
각
중괄호 안의 식은
그러므로
Redefining the Determinant✔
정리 4.4
-
이 정리는 행렬식을 1행에 대한 여인수 전개로 얻을 수 있을 뿐만 아니라 임의의 행에 대한 여인수 전개로 구할 수 있음을 말해준다.
또한 정리 4.8 에 의하여 임의의 열에 대한 여인수 전개로도 행렬식을 구할 수 있음을 알 수 있다.
-
증명
정리 4.3 보조정리 1 은
정리 4.4 따름정리
-
증명
정리 4.5
행렬
-
이 정리는 1형 기본행연산과 행렬식 사이의 관계를 말해준다.
-
증명
즉,
정리 4.6
행렬
-
이 정리는 3형 기본행연산과 행렬식 사이의 관계를 말해준다.
-
증명
Determinant and Rank✔
정리 4.6 따름정리
-
정리 4.2 는
-
증명
Determinant and Elementary Operation✔
기본행[열]연산과 행렬식의 관계
기본행[열]연산과
-
-
-
-
증명
정리 4.3(2형 기본행연산과 행렬식의 관계), 정리 4.5(1형 기본행연산과 행렬식의 관계), 정리 4.6(3형 기본행연산과 행렬식의 관계) 에 의하여 증명된다.
Determinant of Upper Triangular Matrix✔
문제 4.2-23
상삼각행렬
-
정사각행렬은 1형과 3형 기본행연산을 통하여 상삼각행렬이 된다. 그러므로 정사각행렬의 행렬식을 쉽게 구할 수 있다.
지금까지의 정리들은 여인수 전개를 통해 행렬식을 귀납적으로 구하는 것이 매우 번거롭기 때문에 행렬식을 효과적으로 구할 수 있도록 기본연산과 행렬식 간의 관계를 밝히기 위한 것들이었다.
그리고 이 정리는 상삼각행렬의 행렬식이 쉽게 구해질 수 있다는 것을 말해줌으로써 기본연산의 목표를 상삼각행렬을 만드는 것으로 두는 것이 좋다는 결론을 알려준다.
-
증명
-
안 좋은 증명(이렇게 증명하는 건 대각성분이
상삼각행렬
위 과정은 다음 연산을 반복한 것에 불과하다.
-
-
-
먼저
-
-
-
이를 통하여 행렬식
그러므로 다음이 성립한다.
-
-
예시
삼각행렬
-
증명
상삼각행렬일 경우 문제 4.2-23 에서 증명이 끝났다. ▲
하삼각행렬일 경우 문제 4.2-23 의 증명과정과 거의 비슷하게 증명 가능하다. ■
Determinant of Elementary Matrix✔
기본행렬의 행렬식(Determinant of Elementary Matrix)
-
-
-
-
증명
행렬식과 기본행연산의 관계와
정리 4.7
-
이 정리는 행렬식이 곱을 보존하는 함수임을 말해준다.
-
증명
이렇게
정리 4.6 따름정리 에 의하여
그러므로
정리 4.7 따름정리
-
-
-
증명
이는
문제 4.2-29
기본행렬
-
증명
모든 행이 서로 같으므로
모든 행이 서로 같으므로
이제 기본행연산을 한번 적용한 기본행렬의 행렬식이 전치행렬의 행렬식과 같다는 것을 가정할 수 있다.
이제 임의의 기본행렬
기본행연산을 한번만 적용한 기본행렬의 행렬식이 전치행렬의 행렬식이 같다는 것과 정리 4.7 에 의하여 다음이 성립한다.
이로써 모든 증명이 끝났다. ■
Determinant of Transpose✔
정리 4.8
-
지금까지의 정리들은 행에 대한 여인수 전개, 기본행연산과 행렬식의 관계 등등 행의 관점에서 행렬식을 연구한 결과이다. 그러나 이 정리는 지금까지의 정리들이 열의 관점에서도 그대로 성립함을 말해준다.
즉, 열에 대한 여인수 전개로도 행렬식을 구할 수 있다. 또한 기본행연산 대신 기본열연산을 사용할 수도 있다. 기본열연산에 따른 행렬식의 변화는 기본행연산에 따른 행렬식의 변화와 같기 때문이다.
-
증명
이로써 모든 증명이 끝났다. ■
열에 의한 행렬식
Determinant of Submatrix✔
문제 4.3-20
정사각행렬
-
증명
문제 4.3-21
정사각행렬
-
증명
문제 4.3-20 과 정리 4.7 따름정리에 의하여 다음이 성립한다.
Cramer's Rule✔
정리 4.9 Cramer's Rule
-
이 정리를
-
증명
정리 4.7 은 행렬식의 곱의 보존을 보장한다. 그러므로 다음이 성립한다.
그러므로
-
예시
다음과 같이 행렬표현으로 나타낸 연립일차방정식
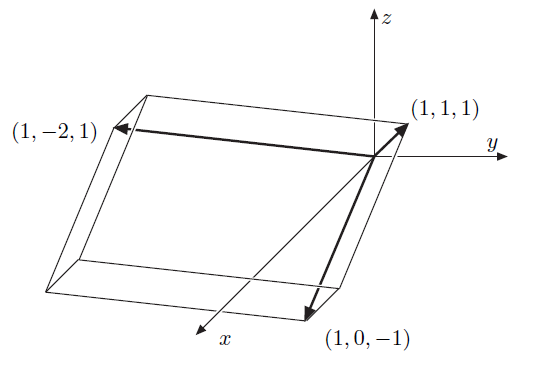
n-dimensional volume of parallelepiped✔
나란히꼴의
행렬
-
-
증명
-
예시
행렬
실제로 다음 그림을 보면 해당 평행육면체의 세 변의 길이는
Determinant of Similar Matrices✔
문제 4.3-15
두 행렬
-
증명
■