Skip to content

Diagonalization

Contents

Diagonalizable✔

선형연산자의 대각화가능(diagonalizable)

유한차원 벡터공간 V\mathbf{V} 의 선형연산자 T⁡\operatorname{T} 에 대하여 [T⁡]β[\operatorname{T} ]_{\beta } 가 대각행렬이 되도록 하는 V\mathbf{V} 의 순서기저 β\beta 가 존재하면 T⁡\operatorname{T} 를 대각화가능하다고 한다.

  • 유한차원 벡터공간 V\mathbf{V} 의 선형연산자 T⁡\operatorname{T} 를 대각화가능하게 만드는, 즉 [T⁡]β[\operatorname{T} ]_{\beta} 가 대각행렬이 되게 하는 순서기저 β={v1,v2,…,vn}\beta = \{v_1, v_2, \dots, v_n \} 를 찾아보자. D=[T⁡]βD = [\operatorname{T} ] _{\beta } 가 대각행렬이면 선형변환의 행렬표현 에 의하여 vj∈βv_j \in \beta 와 λj=Djj\lambda _j = D _{jj} 에 대하여 T⁡(vj)=∑i=1nDijvj=λjvj\operatorname{T} (v_j) = \displaystyle \sum_{i=1}^{n}D _{ij}v_j = \lambda _jv_j 이다.

    역으로 스칼라 λ1,λ2,…,λn\lambda _1, \lambda _2, \dots, \lambda _n 에 대하여 β\beta 가 T⁡(vj)=λjvj\operatorname{T} (v_j) = \lambda _jv_j 를 만족하면 다음이 성립한다.

    [T⁡]β=(λ10…00λ2…0⋮⋮⋱⋮00…λn) [\operatorname{T} ]_{\beta } = \begin{pmatrix} \lambda _{1}&0&\dots&0\\ 0&\lambda _2&\dots&0\\ \vdots& \vdots& \ddots& \vdots \\ 0&0&\dots&\lambda _n\\ \end{pmatrix}

    선형연산자 T⁡\operatorname{T} 가 대각화가능이면 기저 β\beta 의 각 벡터 vv 는 적절한 스칼라 λ\lambda 에 대하여 T⁡(v)=λv\operatorname{T} (v) = \lambda v 를 만족한다. vv 는 기저의 원소이므로 영벡터가 아니다. 이를 기반으로 고유벡터의 정의를 내릴 수 있다.

정사각행렬의 대각화가능(diagonalizable)

선형연산자 L⁡A\operatorname{L}_{A} 가 대각화가능이면 정사각행렬 AA 를 대각화가능이라고 한다.

Eigenvector✔

선형연산자의 고유벡터(eigenvector) 와 고윳값(eigenvalue)

벡터공간 V\mathbf{V} 의 선형연산자 T⁡\operatorname{T} 에 대하여 다음과 같이 정의한다.

  • 영벡터가 아닌 벡터 v∈Vv \in \mathbf{V} 와 스칼라 λ\lambda 에 대하여 T⁡(v)=λv\operatorname{T} (v) = \lambda v 이면 벡터 vv 를 T⁡\operatorname{T} 의 고유벡터라 한다.

  • 스칼라 λ\lambda 를 고유벡터 vv 에 대응하는 고윳값이라 한다.
  • 고유벡터는 특성벡터(characteristic vector, proper vector), 고윳값은 특성값(characteristic value, proper value) 라고도 부른다.

정사각행렬의 고유벡터(eigenvector) 와 고윳값(eigenvalue)

행렬 A∈Fn×nA \in \mathbf{F}^{n \times n} 에 대하여 다음과 같이 정의한다.

  • L⁡A\operatorname{L}_{A} 의 고유벡터, 즉 스칼라 λ\lambda 에 대하여 Av=λvAv = \lambda v 를 만족하는 영벡터가 아닌 벡터 v∈Fnv \in \mathbf{F} ^{n} 을 AA 의 고유벡터라 한다.

  • 스칼라 λ\lambda 를 고유벡터 vv 에 대응하는 행렬 AA 의 고윳값이라 한다.

Properties of eigenvector✔

정리 5.1

유한차원 벡터공간 V\mathbf{V} 의 선형연산자 T⁡\operatorname{T} 가 대각화가능인 것과 T⁡\operatorname{T} 의 고유벡터로 이루어진 V\mathbf{V} 의 순서기저 β\beta 가 존재하는 것은 동치이다.

즉, β={v1,v2,…,vn}\beta = \{v_1, v_2, \dots, v_n \} 가 T⁡\operatorname{T} 의 고유벡터로 이루어진 V\mathbf{V} 의 순서기저이면 D=[T⁡]βD = [\operatorname{T} ] _{\beta} 는 대각행렬이며 DjjD _{jj} 는 vjv_j 에 대응하는 고윳값이다.

정리 5.1 따름정리

행렬 A∈Fn×nA \in \mathbf{F}^{n \times n} 가 대각화가능인 것과 AA 의 고유벡터로 이루어진 Fn\mathbf{F} ^{n} 의 순서기저가 존재하는 것은 동치이다.

{v1,v2,…,vn}\{v_1, v_2, \dots, v_n\} 를 AA 의 고유벡터로 이루어진 Fn\mathbf{F} ^{n} 의 순서기저라고 하면 jj 열이 벡터 vjv_j 인 n×nn \times n 행렬 QQ 에 대하여 D=Q−1AQD = Q ^{-1}AQ 는 대각행렬이며 DjjD _{jj} 는 vjv_j 에 대응하는 AA 의 고윳값이다.

  • 이 정리는 행렬 AA 가 대각화가능인 것과 대각행렬과 닮음인 것이 동치임을 말해준다.

  • 선형연산자를 대각화한 행렬이 D=[T⁡]βD = [\operatorname{T} ]_{\beta } 인데, 정사각행렬을 대각화한 행렬이 D=Q−1AQD = Q ^{-1}AQ 인 이유는 정리 2.23 따름정리 에서 바로 나온다.

  • 예시

    행렬 A=(1342)A = \begin{pmatrix} 1&3\\ 4&2\\ \end{pmatrix} 와 벡터 v1=(1−1),v2=(34)v_1 = \begin{pmatrix} 1\\ -1\\ \end{pmatrix}, v_2 = \begin{pmatrix} 3\\ 4\\ \end{pmatrix} 에 대하여 다음이 성립한다.

    L⁡A(v1)=(−22)=−2v1 \operatorname{L}_{A}(v_1) = \begin{pmatrix} -2\\ 2\\ \end{pmatrix} = -2v_1
    L⁡A(v2)=(1520)=5v2 \operatorname{L}_{A}(v_2) = \begin{pmatrix} 15\\ 20\\ \end{pmatrix} = 5v_2

    그러므로 v1,v2v_1, v_2 는 L⁡A\operatorname{L}_{A} 와 AA 의 고유벡터이다. v1,v2v_1, v_2 에 대응하는 고윳값은 λ1=−2,λ2=5\lambda _1 = -2, \lambda _2 = 5 이다.

    이때 β={v1,v2}\beta = \{v_1, v_2\} 는 AA 와 L⁡A\operatorname{L}_{A} 의 고유벡터로 이루어진 R2\R ^{2} 의 순서기저이다. 따라서 AA 와 L⁡A\operatorname{L}_{A} 는 대각화가능이다.

    또한 정리 5.1 과 따름정리에 의하여 Q=(13−14)Q = \begin{pmatrix} 1&3\\ -1&4\\ \end{pmatrix} 에 대하여 Q−1AQ=[L⁡A]β=(−2005)Q ^{-1}AQ = [\operatorname{L}_{A}]_{\beta } = \begin{pmatrix} -2&0\\ 0&5\\ \end{pmatrix} 이다.

  • numpy 로 검증

    A = np.array([[1,3], 
              [4,2]])
eigval, eigvec = np.linalg.eig(A)
print(eigval)
print(eigvec)

    [-2.  5.]
[[-0.70710678 -0.6       ]
 [ 0.70710678 -0.8       ]]

고유벡터와 고윳값을 가지지 않는 선형연산자나 행렬이 존재한다.

  • 증명

    R2\R ^{2} 의 벡터를 π2\dfrac{\pi }{2} 만큼 회전시키는 선형연산자 T⁡\operatorname{T} 와 영이 아닌 벡터 v∈R2v \in \R ^{2} 에 대하여 T⁡(v)\operatorname{T} (v) 는 00 과 vv 를 지나는 직선 위에 있지 않다.

    이는 T⁡(v)\operatorname{T} (v) 를 vv 의 스칼라배로 표현할 수 없다는 것이다. 따라서 T⁡\operatorname{T} 는 고유벡터와 고윳값을 가지지 않으며, 대각화 불가능하다.

Characteristic polynomial (Finding eigenvalue)✔

정리 5.2

행렬 A∈Fn×nA \in \mathbf{F}^{n \times n} 에 대하여 스칼라 λ\lambda 가 AA 의 고윳값인 것과 det⁡(A−λIn)=0\det(A - \lambda I_n) = 0 인 것은 동치이다.

  • 이 정리는 고윳값을 계산하는 방법을 제시한다.

  • 이 정리는 특성다항식의 근을 찾으면 유한차원 벡터공간의 행렬 또는 선형연산자의 고윳값을 모두 밝힐 수 있음을 말해준다.

  • 증명

    스칼라 λ\lambda 가 AA 의 고윳값임을 가정하자. 스칼라 λ\lambda 가 AA 의 고윳값인 것과 Av=λvAv = \lambda v 인 영이 아닌 벡터 v∈Fnv \in \mathbf{F} ^{n} 가 존재하는 것은 동치이다. 그러므로 (A−λIn)(v)=0(A - \lambda I_n) (v) = 0 이다.

    A−λInA - \lambda I_n 이 가역이면 v=0v = 0 이므로 모순이다. 즉, A−λInA - \lambda I_n 는 가역이 아니다. 정리 4.7 따름정리 에 의하여 det⁡(A−λIn)=0\det(A - \lambda I_n) = 0 이다.

정사각행렬의 특성다항식(Characteristic polynomial)

행렬 A∈Fn×nA \in \mathbf{F}^{n \times n} 에 대하여 AA 의 특성다항식은 다항식 f(t)=det⁡(A−tIn)f(t) = \det(A - tI_n) 이다.

  • 정리 5.2 는 행렬의 고윳값이 특성다항식의 근임을 말해준다. 이는 특성다항식의 계산을 통하여 행렬 또는 선형연산자의 모든 고윳값을 얻을 수 있음을 뜻한다.

  • 이때 A−tIn∉Fn×nA - tI_n \not\in \mathbf{F}^{n \times n} 이다. 행렬 A−tInA - tI_n 는 F\mathbf{F} 를 계수로 가지는 tt 에 대한 유리식으로 이루어진 체 F(t)\mathbf{F} (t) 에 속해있다. 즉, A−tIn∈F(t)n×nA - tI_n \in \mathbf{F}(t)^{n \times n} 이다.

    행렬식에 대한 정리들을 F(t)\mathbf{F} (t) 에서도 사용할 수 있다.

  • 예시

    행렬 A=(1141)∈R2×2A = \begin{pmatrix} 1&1\\ 4&1\\ \end{pmatrix} \in \R ^{2 \times 2} 의 고윳값을 구하기 위하여 다음 특성다항식을 풀어보자.

    det⁡(A−tI2)=det⁡(1−t141−t)=t2−2t−3=(t−3)(t+1) \det(A - tI_2) = \det \begin{pmatrix} 1-t&1\\ 4&1-t\\ \end{pmatrix} = t ^{2} - 2t - 3 = (t - 3)(t + 1)

    정리 5.2 에 의하여 AA 의 고윳값은 3,−13, -1 뿐이다.

  • numpy 로 검증

    A = np.array([[1,1], 
              [4,1]])
eigval, eigvec = np.linalg.eig(A)
print(eigval)
print(eigvec)

    [ 3. -1.]
[[ 0.4472136  -0.4472136 ]
 [ 0.89442719  0.89442719]]

선형연산자의 행렬식(determinant)

유한차원 벡터공간 V\mathbf{V} 의 선형연산자 T⁡\operatorname{T} 와 V\mathbf{V} 의 순서기저 β\beta 에 대하여 T⁡\operatorname{T} 의 행렬식을 다음과 같이 정의한다.

det⁡(T⁡):=det⁡([T⁡]β) \det(\operatorname{T} ) := \det([\operatorname{T} ]_{\beta })

선형연산자의 특성다항식(Characteristic polynomial)

유한차원 벡터공간 V\mathbf{V} 의 선형연산자 T⁡\operatorname{T} 와 V\mathbf{V} 의 순서기저 β\beta 에 대하여 T⁡\operatorname{T} 의 특성다항식을 다음과 같이 정의한다.

f(t)=det⁡([T⁡]β−tIn) f(t) = \det([\operatorname{T} ]_{\beta } - tI_n)

문제 5.1-13

닮은 행렬은 같은 특성다항식을 가진다.

유한차원 벡터공간 V\mathbf{V} 의 선형연산자의 행렬식과 특성다항식의 정의는 V\mathbf{V} 의 기저의 선택에 관계없다.

  • 이 정리는 선형연산자의 행렬식과 특성다항식의 정의의 기저로 어떤 기저를 선택하든 관계없다는 것을 말해준다.

  • 증명

    A,BA, B 가 닮음이면 가역행렬 QQ 에 대하여 B=Q−1AQB = Q ^{-1}AQ 이다. 그러므로 다음이 성립한다.

    Q−1(A−tIn)Q=Q−1AQ−tQ−1InQ=B−tIn Q ^{-1}(A-tI_n)Q = Q ^{-1}AQ - t Q ^{-1}I_nQ = B - tI_n

    그러므로 A−tInA-tI_n 과 B−tInB-tI_n 은 닮음이다. 따라서 문제 4.3-15 에 의하여 다음이 성립한다.

    det⁡(A−tIn)=det⁡(B−tIn) \det(A -tI_n) = \det(B-tI_n)

    한편 정리 2.23 은 선형연산자의 서로 다른 순서기저에 의한 행렬표현이 서로 닮음임을 말해준다. 그러므로 모든 증명이 끝났다. ■

  • 예시

    벡터공간 P2(R)\mathbf{P}_{2}(\R) 의 선형연산자 T⁡(f(x))=f(x)+(x+1)f′(x)\operatorname{T} (f(x)) = f(x) + (x+1) f'(x) 의 고윳값을 P2(R)\mathbf{P}_{2}(\R) 의 표준순서기저 β\beta 로 구해보자. 다음이 성립한다.

    T⁡(1)=1+(x+1)⋅0=1 \operatorname{T} (1) = 1 + (x + 1) \cdot 0 = 1
    T⁡(x)=x+(x+1)⋅1=1+2x \operatorname{T} (x) = x + (x + 1) \cdot 1 = 1 + 2x
    T⁡(x2)=x2+(x+1)⋅2x=0+2x+3x2 \operatorname{T} (x ^{2}) = x ^{2} + (x + 1) \cdot 2x = 0 + 2x + 3x ^{2}
    [T⁡]β=(110022003) [\operatorname{T} ]_{\beta } = \begin{pmatrix} 1&1&0\\ 0&2&2\\ 0&0&3\\ \end{pmatrix}

    선형연산자 T⁡\operatorname{T} 의 특성다항식의 정의와 문제 4.2-23 에 의하여 다음이 성립한다.

    det⁡([T⁡]β−tI3)=det⁡(1−t1002−t2003−t)=(1−t)(2−t)(3−t)=−(t−1)(2−t)(3−t) \begin{align}\begin{split} \det([\operatorname{T} ]_{\beta } - tI_3) &= \det \begin{pmatrix} 1-t&1&0\\ 0&2-t&2\\ 0&0&3-t\\ \end{pmatrix} \\ &= (1-t)(2-t)(3-t)\\ &= -(t-1)(2-t)(3-t)\\ \end{split}\end{align} \tag*{}

    정리 5.2 에 의하여 선형연산자 T⁡\operatorname{T} 또는 행렬 [T⁡]β[\operatorname{T} ]_{\beta } 의 고윳값은 1,2,31,2,3 뿐이다.

  • numpy

    A = np.array([[1,1,0], 
              [0,2,2],
              [0,0,3]])
eigval, eigvec = np.linalg.eig(A)
print(eigval)
print(eigvec)   

    [1. 2. 3.]
[[1.         0.70710678 0.40824829]
 [0.         0.70710678 0.81649658]
 [0.         0.         0.40824829]]

정리 5.3

행렬 A∈Fn×nA \in \mathbf{F}^{n \times n} 에 대하여 다음이 성립한다.

  1. AA 의 특성다항식은 nn차 다항식이고, 최고차항의 계수는 (−1)n(-1) ^{n} 이다.

  2. AA 에는 최대 nn 개의 서로 다른 고윳값이 있다.

  • 증명

    n=1n = 1 을 가정하자. A=(A11)∈F1×1A = (A _{11}) \in \mathbf{F} ^{1 \times 1} 의 특성다항식은 다음과 같다.

    det⁡(A−tI1)=det⁡((A11−t))=A11−t \det(A - tI_1) = \det((A _{11} - t)) = A _{11} - t

    n=1n = 1 일 때 AA 의 특성다항식은 11차 다항식이고, 최고차항의 계수가 (−1)1=−1(-1) ^{1} = -1 이다. 또한 정리 5.2 에 의하여 11차 다항식이 최대 11 개의 서로 다른 근을 가지기 때문에 AA 는 최대 11 개의 서로 다른 고윳값을 가진다. ▲

    n−1n - 1 에 대하여 정리가 성립함을 가정하고 nn 에 대하여 정리가 성립함을 보이면 증명이 끝난다. A∈Fn×nA \in \mathbf{F}^{n \times n} 에 대하여 B=A−tInB = A - tI_n 로 두면 AA 의 특성다항식은 다음과 같다.

    det⁡(B)=(−1)1+1(A11−t)⋅det⁡(B~11)+∑j=2n(−1)1+jA1j⋅det⁡(B~1j)=(−1)1+1(−t)det⁡(B~11)+(−1)1+1(A11)det⁡(B~11)+∑j=2n(−1)1+jA1j⋅det⁡(B~1j)=−t⋅det⁡(B~11)+∑j=1n(−1)1+jA1j⋅det⁡(B~1j) \begin{align}\begin{split} \det(B) &= (-1) ^{1 + 1} (A _{11} - t) \cdot \det(\tilde{B}_{11}) + \sum_{j=2}^{n}(-1) ^{1+j} A _{1j} \cdot \det(\tilde{B}_{1j}) \\ &= (-1) ^{1+1}(-t)\det(\tilde{B}_{11}) + (-1) ^{1+1}(A _{11})\det(\tilde{B}_{11}) + \sum_{j=2}^{n}(-1) ^{1+j} A _{1j} \cdot \det(\tilde{B}_{1j}) \\ &= -t \cdot \det(\tilde{B}_{11}) + \sum_{j=1}^{n}(-1) ^{1+j} A _{1j} \cdot \det(\tilde{B}_{1j}) \\ \end{split}\end{align} \tag*{}

    det⁡(B~1j)\det(\tilde{B}_{1j}) 는 (n−1)×(n−1)(n-1) \times (n-1) 행렬의 특성다항식이다. n−1n - 1 에 대하여 정리가 성립하므로 det⁡(B~1j)\det(\tilde{B}_{1j}) 는 n−1n-1 차 다항식이고, 최고차항의 계수가 (−1)n−1(-1) ^{n-1} 이다. ∑j=1n(−1)1+jA1j\displaystyle \sum_{j=1}^{n}(-1) ^{1+j}A _{1j} 은 스칼라이므로 −t⋅det⁡(B~11)-t \cdot \det(\tilde{B}_{11}) 에 의하여 det⁡(B)\det(B) 는 최고차항의 계수가 (−1)n(-1) ^{n} 인 nn 차 다항식이 된다. 또한 정리 5.2 에 의하여 nn차 다항식이 최대 nn 개의 서로 다른 근을 가지기 때문에 AA 는 최대 nn 개의 서로 다른 고윳값을 가진다. ■

Finding eigenvector✔

정리 5.4

행렬 A∈Fn×nA \in \mathbf{F}^{n \times n} 와 고윳값 λ\lambda 에 대하여 벡터 v∈Fnv \in \mathbf{F} ^{n} 가 λ\lambda 에 대응하는 AA 의 고유벡터인 것과 v≠0∧(A−λI)v=0v \neq 0 \land (A-\lambda I)v = 0 인 것은 동치이다.

  • 이 정리는 고윳값에 대응하는 고유벡터를 찾는 방법을 알려준다.

  • 증명

    vv 가 고윳값 λ\lambda 에 대응하는 AA 의 고유벡터이면 고유벡터의 정의에 의하여 Av=λv⟹(A−λI)v=0Av = \lambda v \implies (A - \lambda I)v = 0 와 v≠0v \neq 0 이 성립한다.

    역으로 영벡터가 아닌 벡터 vv 에 대하여 (A−λI)v=0⟹Av=λv(A - \lambda I)v = 0 \implies Av = \lambda v 가 성립하면 고유벡터의 정의에 의하여 vv 는 고윳값 λ\lambda 에 대응하는 고유벡터이다.

  • 예시

    행렬 A=(1141)A = \begin{pmatrix} 1&1\\ 4&1\\ \end{pmatrix} 의 모든 고유벡터를 구해보자. AA 의 고윳값은 λ1=3,λ2=−1\lambda _1 = 3, \lambda _2 = -1 이다.

    B1=A−λ1I=(−214−2)B_1 = A - \lambda _1I = \begin{pmatrix} -2&1\\ 4&-2\\ \end{pmatrix} 를 정의하면 λ1\lambda _1 에 대응하는 고유벡터 x=(x1x2)∈R2x = \begin{pmatrix} x_1\\ x_2\\ \end{pmatrix} \in \R ^{2} 는 x≠0∧x∈ker⁡(L⁡B1)x \neq 0 \land x \in \ker (\operatorname{L} _{B_1}) 을 만족한다. 즉, 다음이 성립해야 한다.

    (−214−2)(x1x2)=(−2x1+x24x1−2x2)=(00) \begin{pmatrix} -2&1\\ 4&-2\\ \end{pmatrix}\begin{pmatrix} x_1\\ x_2\\ \end{pmatrix}= \begin{pmatrix} -2x_1+x_2\\ 4x_1-2x_2\\ \end{pmatrix}= \begin{pmatrix} 0\\ 0\\ \end{pmatrix}

    이 방정식의 해집합은 t∈Rt \in \R 에 대하여 t(12)t \begin{pmatrix} 1\\ 2\\ \end{pmatrix} 이므로 t≠0t \neq 0 에 대하여 x=t(12)x = t \begin{pmatrix} 1\\ 2\\ \end{pmatrix} 는 λ1\lambda _1 에 대응하는 고유벡터이다. ▲

    B2=A−λ2I=(2142)B_2 = A - \lambda _2I = \begin{pmatrix} 2&1\\ 4&2\\ \end{pmatrix} 를 정의하면 λ2\lambda _2 에 대응하는 고유벡터 x=(x1x2)∈R2x = \begin{pmatrix} x_1\\ x_2\\ \end{pmatrix} \in \R ^{2} 는 x≠0∧x∈ker⁡(L⁡B2)x \neq 0 \land x \in \ker (\operatorname{L} _{B_2}) 을 만족한다. 즉, 다음이 성립해야 한다.

    (2142)(x1x2)=(2x1+x24x1+2x2)=(00) \begin{pmatrix} 2&1\\ 4&2\\ \end{pmatrix}\begin{pmatrix} x_1\\ x_2\\ \end{pmatrix}= \begin{pmatrix} 2x_1+x_2\\ 4x_1+2x_2\\ \end{pmatrix}= \begin{pmatrix} 0\\ 0\\ \end{pmatrix}

    이 방정식의 해집합은 t∈Rt \in \R 에 대하여 t(1−2)t \begin{pmatrix} 1\\ -2\\ \end{pmatrix} 이므로 t≠0t \neq 0 에 대하여 x=t(1−2)x = t \begin{pmatrix} 1\\ -2\\ \end{pmatrix} 는 λ2\lambda _2 에 대응하는 고유벡터이다. ▲

    집합 {(12),(1−2)}\bigg \{\begin{pmatrix} 1\\ 2\\ \end{pmatrix}, \begin{pmatrix} 1\\ -2\\ \end{pmatrix}\bigg \} 은 일차독립이고 기수가 22 이므로 정리 1.10 따름정리 2 에 의하여 기저이다. 이 기저는 AA 의 고유벡터로 이루어진 기저이므로 AA 와 L⁡A\operatorname{L}_{A} 는 대각화가능하다.

  • numpy 로 검증

    A = np.array([[1,1], 
              [4,1]])
eigval, eigvec = np.linalg.eig(A)
print(eigval)
print(eigvec)

    [ 3. -1.]
[[ 0.4472136  -0.4472136 ]
 [ 0.89442719  0.89442719]]

    고윳값 33 에 대응되는 고유벡터 (12)\begin{pmatrix} 1\\ 2\\ \end{pmatrix} 가 같은 열에 나오고, 고윳값 −1-1 에 대응되는 고유벡터 (1−2)\begin{pmatrix} 1\\ -2\\ \end{pmatrix} 도 같은 열에 나온다.

차원이 각각 nn 이고 순서기저가 β\beta 인 벡터공간 V\mathbf{V} 와 선형변환 T⁡:V→V\operatorname{T} : \mathbf{V} \to \mathbf{V} 와 행렬 A=[T⁡]βA = [\operatorname{T} ]_{\beta} 에 대하여 다음이 성립한다. 즉, L⁡A∘ϕβ=ϕβ∘T⁡\operatorname{L}_{A} \circ \phi _{\beta } = \phi _{\beta } \circ \operatorname{T} 이다.

V→T⁡Vϕβ↓↓ϕβFn→L⁡AFn \begin{CD} \mathbf{V} @> \operatorname{T} >> \mathbf{V} \\ @V \phi _{\beta } VV @VV \phi _{\beta } V \\ \mathbf{F} ^{n} @> \operatorname{L}_{A} >> \mathbf{F} ^{n} \end{CD}

이때 다음이 성립한다.

  1. v∈Vv \in \mathbf{V} 가 λ\lambda 에 대응하는 T⁡\operatorname{T} 의 고유벡터인 것과 ϕβ(v)\phi _{\beta }(v) 가 λ\lambda 에 대응하는 AA 의 고유벡터인 것은 동치이다.

  2. AA 와 T⁡\operatorname{T} 의 고윳값 λ\lambda 에 대하여 벡터 y∈Fny \in \mathbf{F} ^{n} 가 λ\lambda 에 대응하는 AA 의 고유벡터인 것과 ϕβ−1(y)\phi _{\beta } ^{-1}(y) 가 λ\lambda 에 대응하는 T⁡\operatorname{T} 의 고유벡터인 것은 동치이다.

  • 이 정리는 유한차원 벡터공간에서 정의된 선형연산자의 고유벡터를 찾는 것을 행렬의 고유벡터를 찾는 것으로 귀결시킬 수 있음을 말해준다.

  • 증명

    첫번째 명제는 그림 2.2 에서 V=W,γ=β\mathbf{V} = \mathbf{W}, \gamma = \beta 인 경우이다. ▲

    두번째 명제를 보이자. vv 가 λ\lambda 에 대응하는 T⁡\operatorname{T} 의 고유벡터임을 가정하자. 그러면 T⁡(v)=λv\operatorname{T} (v) = \lambda v 이고 첫번째 명제에 의하여 다음이 성립한다.

    Aϕβ(v)=L⁡Aϕβ(v)=ϕβT⁡(v)=ϕβ(λv)=λϕβ(v) A \phi _{\beta }(v) = \operatorname{L}_{A}\phi _{\beta }(v) = \phi _{\beta }\operatorname{T} (v) = \phi _{\beta }(\lambda v) = \lambda \phi _{\beta }(v)

    ϕβ\phi _{\beta } 는 동형사상이므로 단사이고 v=0v = 0 일 때에만 ϕβ(v)=0\phi _{\beta }(v) = 0 이다. vv 가 고유벡터임을 가정했으므로 v≠0v \neq 0 이므로 ϕβ(v)≠0\phi _{\beta }(v) \neq 0 이다. 따라서 ϕβ(v)\phi _{\beta }(v) 는 AA 의 고유벡터이다.

    역으로 ϕβ(v)\phi _{\beta }(v) 가 AA 의 고유벡터이면 vv 가 λ\lambda 에 대응하는 T⁡\operatorname{T} 의 고유벡터임을 비슷한 논리로 쉽게 보일 수 있다. ▲

    세번째 명제는 두번째 명제에서 바로 나온다. ■

  • 예시

    P2(R)\mathbf{P}_{2}(\R) 의 선형연산자 T⁡(f(x))=f(x)+(x+1)f′(x)\operatorname{T} (f(x)) = f(x) + (x+1)f'(x) 의 고윳값은 1,2,31, 2, 3 이다.

    λ1=1\lambda _1 = 1 에 대응하는 AA 의 고유벡터는 a≠0a \neq 0 에 대하여 a(100)=ae1a \begin{pmatrix} 1\\ 0\\ 0\\ \end{pmatrix}=ae_1 이다. β\beta 를 P2(R)\mathbf{P}_{2}(\R) 의 표준순서기저로 두었을 때 λ1=1\lambda _1 = 1 에 대응하는 T⁡\operatorname{T} 의 고유벡터는 다음과 같다.

    ϕβ−1(ae1)=aϕβ−1=a⋅1=a \phi ^{-1} _{\beta } (ae_1) = a \phi ^{-1}_{\beta } = a \cdot 1 = a

    λ2=2\lambda _2 = 2 에 대하여 정리 5.4 를 통하여 고유벡터를 찾기 위해 다음과 같은 행렬 B2B_2 를 정의하면 ker⁡(L⁡B2)={a(110):a∈R}\ker (\operatorname{L}_{B_2}) = \bigg \{a \begin{pmatrix} 1\\ 1\\ 0\\ \end{pmatrix}:a \in \R\bigg \} 이다.

    B2=A−λ2I=(−110002001) B_2 = A - \lambda _2I=\begin{pmatrix} -1&1&0\\ 0&0&2\\ 0&0&1\\ \end{pmatrix}

    따라서 λ2=2\lambda _2 = 2 에 대응하는 T⁡\operatorname{T} 의 고유벡터는 a≠0a \neq 0 에 대하여 다음과 같다.

    ϕβ−1(a(110))=aϕβ−1(e1+e2)=a(1+x) \phi _{\beta }^{-1}\bigg (a \begin{pmatrix} 1\\ 1\\ 0\\ \end{pmatrix}\bigg ) = a \phi _{\beta }^{-1}(e_1+e_2) = a(1+x)

    λ3=3\lambda _3 = 3 에 대응하는 T⁡\operatorname{T} 의 고유벡터는 a≠0a \neq 0 에 대하여 a(1+2x+x2)a(1+2x+x ^{2}) 이다.

    a=1a = 1 인 고유벡터 집합 γ={1,1+x,1+2x+x2}\gamma = \{1, 1+x, 1+2x+x ^{2}\} 는 T⁡\operatorname{T} 의 고유벡터로 이루어진 P2(R)\mathbf{P}_{2}(\R) 의 순서기저이므로 T⁡\operatorname{T} 를 다음과 같이 대각화할 수 있다.

    [T⁡]γ=(100020003) [\operatorname{T} ]_{\gamma } = \begin{pmatrix} 1&0&0\\ 0&2&0\\ 0&0&3\\ \end{pmatrix}

  • numpy

    A = np.array([[1,1,0], 
              [0,2,2],
              [0,0,3]])
eigval, eigvec = np.linalg.eig(A)
print(eigval)
print(eigvec)   

    [1. 2. 3.]
[[1.         0.70710678 0.40824829]
 [0.         0.70710678 0.81649658]
 [0.         0.         0.40824829]]

    각 고윳값의 고유벡터가 같은 열에 나온다.

Geometric Interpretation of Eigenvector of Linear Operator✔

R\R-벡터공간 V\mathbf{V} 의 선형연산자 T⁡\operatorname{T} 의 고유벡터 vv, 대응하는 고윳값 λ\lambda 와 vv 에 의해 생성된 V\mathbf{V} 의 1차원 부분공간 W=span⁡({v})\mathbf{W} = \operatorname{span} (\{v\}) 은 00 과 vv 를 지나는 직선이다. 이때 다음이 성립한다.

  1. λ>1\lambda > 1 일 때 T⁡\operatorname{T} 는 W\mathbf{W} 의 벡터를 00 에서 밀어낸다.

  2. λ=1\lambda = 1 일 때 T⁡\operatorname{T} 는 W\mathbf{W} 에서 항등연산자이다.

  3. 0<λ<10 < \lambda < 1 일 때 T⁡\operatorname{T} 는 W\mathbf{W} 의 벡터를 00 방향으로 당긴다.

  4. λ=0\lambda = 0 일 때 T⁡\operatorname{T} 는 W\mathbf{W} 에서 영 연산자이다.

  5. λ<0\lambda < 0 일 때 T⁡\operatorname{T} 는 W\mathbf{W} 의 벡터를 00 의 반대 방향으로 옮긴다.

  • 다음 그림이 이 정리를 설명해준다.

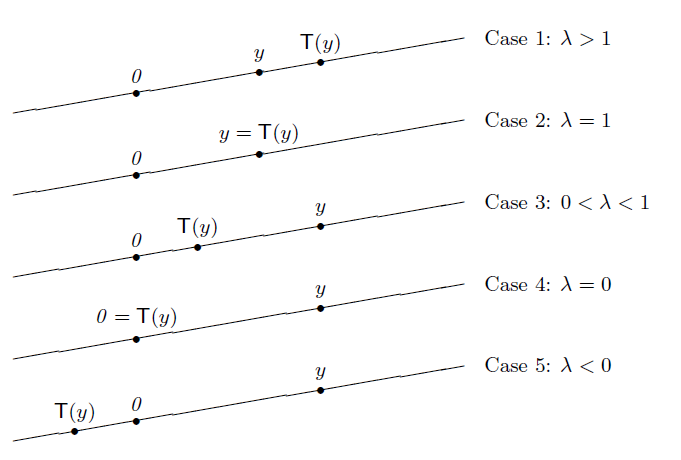
    image

  • 예시

    R2\R ^{2} 의 xx 축 대칭 T⁡(a1,a2)=(a1,−a2)\operatorname{T} (a_1, a_2) = (a_1, -a_2) 은 고유벡터 e1,e2e_1, e_2 를 갖는다. 이는 각각 고윳값 1,−11, -1 에 대응한다.

    e1e_1 과 e2e_2 는 각각 1차원 벡터공간 xx 축과 yy 축을 생성한다. T⁡\operatorname{T} 는 xx축에서 항등변환, yy축에서 방향을 바꾸는 변환이다.

Diagonalizability✔

정리 5.5

벡터공간의 선형연산자 T⁡\operatorname{T} 와 T⁡\operatorname{T} 의 서로 다른 고윳값 λ1,λ2,…,λk\lambda_1, \lambda_2, \dots, \lambda_k 에 대하여 λi\lambda_i 에 대응하는 T⁡\operatorname{T} 의 고유벡터로 이루어진 유한집합을 SiS_i 라고 하자. 각 SiS_i 가 일차독립이면 ⋃i=1kSi\displaystyle \bigcup_{i=1}^{k}S_i 도 일차독립이다.

  • 이 정리는 각 고윳값에 대응하는 고유벡터를 하나씩 선택하여 형성한 집합은 반드시 일차독립인 집합을 이룬다는 것을 말해준다.

  • 증명

    k=1k = 1 인 경우 증명할 것이 없다. ▲

    k>1k > 1 을 가정하고 k−1k - 1 에 대하여 정리가 성립함을 가정하자. 또한 서로 다른 kk 개의 고윳값 λ1,λ2,…,λk\lambda_1, \lambda_2, \dots, \lambda_k 에 대하여 Si={vi1,vi1,…,vini}S_i = \{v _{i1},v _{i1},\dots,v _{in _{i}}\} 가 λi\lambda _i 에 대응하는 일차독립인 T⁡\operatorname{T} 의 고유벡터 집합임을 가정하자.

    i∈{1,2,…,k},j∈{1,2,…,ni}i \in \{1,2,\dots,k\}, j \in \{1,2,\dots,n_i\} 에 대하여 다음을 만족하는 스칼라 aija _{ij} 가 존재한다.

    ∑i=1k∑j=1niaijvij=0(1) \sum_{i=1}^{k}\sum_{j=1}^{n_i}a _{ij}v _{ij} = 0 \tag{1}

    vijv _{ij} 는 λi\lambda _i 에 대응하는 T⁡\operatorname{T} 의 고유벡터이므로 양 변에 T⁡−λkI⁡\operatorname{T} - \lambda _k \operatorname{I} 를 적용하면 다음이 성립한다.

    ∑i=1k∑j=1niaij(λi−λk)vij=0⟺∑i=1k−1∑j=1niaij(λi−λk)vij=0 \sum_{i=1}^{k}\sum_{j=1}^{n_i}a _{ij}(\lambda _i - \lambda _k)v _{ij} = 0 \iff \sum_{i=1}^{k-1}\sum_{j=1}^{n_i}a _{ij}(\lambda _i - \lambda _k)v _{ij} = 0

    가정에 의하여 ⋃i=1k−1Si\displaystyle \bigcup_{i=1}^{k-1}S_i 가 일차독립이므로 i∈{1,2,…,k−1}i \in \{1,2,\dots,k-1\} 에 대하여 aij(λi−λk)=0a _{ij}(\lambda _i- \lambda _k) = 0 이다. λ1,λ2,…,λk\lambda_1, \lambda_2, \dots, \lambda_k 는 같지 않으므로 i∈{1,2,…,k−1}i \in \{1,2,\dots,k-1\} 에 대하여 aij=0a _{ij} = 0 이다.

    그러므로 (1)(1) 은 ∑j=1nkakjvkj=0\sum_{j=1}^{n_k}a _{kj}v _{kj} = 0 이 된다. 가정에 의해 SkS_k 는 일차독립이므로 akj=0a _{kj} = 0 이다. 그러므로 모든 증명이 끝났다. ■

정리 5.5 따름정리

nn차원 벡터공간의 선형연산자 T⁡\operatorname{T} 가 서로 다른 nn개의 고윳값을 가지면 T⁡\operatorname{T} 는 대각화가능하다.

  • 증명

    nn차원 벡터공간을 V\mathbf{V} 라 하자. T⁡\operatorname{T} 에서 서로 다른 nn개의 고윳값 λ1,…,λn\lambda _1,\dots,\lambda _n 이 존재함을 가정하자. 각 ii 에 대하여 λi\lambda _i 에 대응하는 고유벡터 viv_i 를 선택한다. 정리 5.5 에 의하여 {v1,v2,…,vn}\{v_1, v_2, \dots, v_n \} 는 일차독립이고 dim⁡(V)=n\dim (\mathbf{V} ) = n 이므로 정리 1.10 따름정리 2 에 의하여 이 집합은 기저이다.

    정리 5.1 에 의하여 T⁡\operatorname{T} 는 대각화가능하다.

  • T⁡\operatorname{T} 가 대각화 가능하면 서로 다른 nn 개의 고윳값을 가지는 것은 아니다. 가령 항등연산자는 하나의 고윳값 λ=1\lambda =1 을 가지지만 대각화가능하다.

  • 예시

    행렬 A=(1111)A = \begin{pmatrix} 1&1\\ 1&1\\ \end{pmatrix} 의(L⁡A\operatorname{L}_{A} 의) 특성다항식은 다음과 같다.

    det⁡(A−tI)=det⁡(1−t111−t)=t(t−2) \det(A-tI) = \det \begin{pmatrix} 1-t&1\\ 1&1-t\\ \end{pmatrix} = t(t-2)

    L⁡A\operatorname{L}_{A} 의 고윳값은 0,20, 2 이고 dim⁡(R2)=2\dim (\R ^{2}) = 2 이므로 L⁡A\operatorname{L}_{A} (와 AA) 는 대각화 가능하다.

  • numpy

    A = np.array([[1,1], 
              [1,1]])
eigval, eigvec = np.linalg.eig(A)
print(eigval)
print(eigvec)

    [2. 0.]
[[ 0.70710678 -0.70710678]
 [ 0.70710678  0.70710678]]

split over✔

체 F\mathbf{F} 위에서 완전히 인수분해됨(split over F\mathbf{F}) 의 정의

다항식 f(t)∈PFf(t) \in \mathbf{P}_{\mathbf{F} } 가 스칼라 c,a1,a2,…,an∈Fc, a_1, a_2, \dots, a_n \in \mathbf{F} 에 대하여 다음을 만족하면 체 F\mathbf{F} 위에서 완전히 인수분해된다고 한다.

f(t)=c(t−a1)(t−a2)…(t−an) f(t) = c(t-a_1)(t-a_2)\dots(t-a_n)

  • 예시

    f(t)=t2−1=(t+1)(t−1)f(t) = t ^{2} - 1 = (t+1)(t-1) 이므로 f(t)f(t) 는 R\R 위에서 완전히 인수분해된다.

    g(t)=t2+1g(t) = t ^{2} + 1 는 R\R 위에서 완전히 인수분해되지 않는다. 그러나 g(t)=(t+i)(t−i)g(t) = (t + i)(t - i) 이므로 g(t)g(t) 는 C\Bbb{C} 위에서 완전히 인수분해된다.

정리 5.6

F\mathbf{F}-벡터공간 V\mathbf{V} 의 대각화가능한 선형연산자의 특성다항식은 F\mathbf{F} 위에서 완전히 인수분해된다.

  • 이 정리는 선형연산자 T⁡\operatorname{T} 의 특성다항식이 중근을 가질 수도 있으므로 대각화가능하기 위하여 서로 다른 nn 개의 고윳값을 가질 필요가 없음을 말해준다.

  • 증명

    nn차원 벡터공간 V\mathbf{V} 의 대각화가능한 선형연산자를 T⁡\operatorname{T} 라 하고 [T⁡]β=D[\operatorname{T} ]_{\beta } = D 가 대각행렬이 되도록 하는 V\mathbf{V} 의 순서기저를 β\beta 라 하면 DD 는 다음과 같다.

    D=(λ10…00λ2…0⋮⋮⋱⋮00…λn) D = \begin{pmatrix} \lambda _{1}&0&\dots&0\\ 0&\lambda _2&\dots&0\\ \vdots& \vdots& \ddots& \vdots \\ 0&0&\dots&\lambda _n\\ \end{pmatrix}

    T⁡\operatorname{T} 의 특성다항식 f(t)f(t) 는 다음과 같다.

    f(t)=det⁡(D−tI)=(λ1−t0…00λ2−t…0⋮⋮⋱⋮00…λn−t)=(λ1−t)(λ2−t)…(λn−t)=(−1)n(t−λ1)(t−λ2)…(t−λn) \begin{align}\begin{split} f(t) &= \det(D-tI) = \begin{pmatrix} \lambda _{1}-t&0&\dots&0\\ 0&\lambda _2-t&\dots&0\\ \vdots& \vdots& \ddots& \vdots \\ 0&0&\dots&\lambda _n-t\\ \end{pmatrix} \\ &= (\lambda _1-t)(\lambda _2-t)\dots(\lambda _n-t)=(-1)^{n}(t-\lambda _1)(t-\lambda _2)\dots(t-\lambda _n) \end{split}\end{align} \tag*{}

    ■

  • 한편 T⁡\operatorname{T} 의 특성다항식이 완전히 인수분해되어도 T⁡\operatorname{T} 가 대각화 불가능일 수도 있다.

문제 5.2-9

유한차원 벡터공간 V\mathbf{V} 의 선형연산자 T⁡\operatorname{T} 에 대하여 [T⁡]β[\operatorname{T}]_{\beta } 가 상삼각행렬이 되게 하는 순서기저 β\beta 가 존재하면 T⁡\operatorname{T} 의 특성다항식이 완전히 인수분해된다.

상삼각행렬 A∈Fn×nA \in \mathbf{F}^{n \times n} 의 특성다항식은 완전히 인수분해된다.

  • 증명

    dim⁡(V)=n\dim (\mathbf{V}) = n 을 가정하자.

    T⁡\operatorname{T} 의 특성다항식 f(t)=det⁡([T⁡]β−tIn)f(t) = \det([\operatorname{T}]_{\beta } - tI_n) 의 A=[T⁡]β−tInA = [\operatorname{T}]_{\beta }-tI_n 은 상삼각행렬이다. 문제 4.2-23 에 의하여 det⁡(A)=∏i=1nAii\det(A) = \prod_{i=1}^{n}A _{ii} 이다. 따라서 T⁡\operatorname{T} 의 특성방정식은 완전히 인수분해된다. ▲

    상삼각행렬의 특성다항식이 완전히 인수분해된다는 것도 같은 논리로 증명 가능하다. ■

문제 5.2-12

행렬 A∈Fn×nA \in \mathbf{F}^{n \times n} 의 특성다항식이 완전히 인수분해되면 AA 는 상삼각행렬과 닮은 행렬이다.

유한차원 벡터공간 V\mathbf{V} 의 선형연산자 T⁡\operatorname{T} 에 대하여 T⁡\operatorname{T} 의 특성다항식이 완전히 인수분해되면 [T⁡]β[\operatorname{T}]_{\beta } 가 상삼각행렬이 되게 하는 순서기저 β\beta 가 존재한다.

  • 증명

    1:

    n=1n = 1 이면 AA 의 특성다항식은 det⁡(A11−tI1)=A11−tI1\det(A _{11} - tI_1) = A _{11} - tI_1 으로 완전히 인수분해된다. 또한 AA 는 상삼각행렬이다. ▲

    n−1n - 1 에서 정리가 성립함을 가정하고 nn 에 대하여 증명하자. 가정에 의하여 AA 의 특성다항식은 완전히 인수분해된다. 이로써 최소 하나 이상의 고윳값 λ\lambda 가 존재하고 이 고윳값에 대응하는 최소 하나 이상의 고유벡터 v1v_1 가 존재한다.

    {v1}\{v_1\} 을 확장하여 Fn\mathbf{F}^{n} 의 기저 γ={v1,v2,…,vn}\gamma = \{v_1, v_2, \dots, v_n\} 를 만들 수 있다. jj열이 vjv_j 인 n×nn \times n 행렬을 PP 로 두면 [L⁡A]γ=P−1AP[\operatorname{L}_{A}]_{\gamma } = P ^{-1}AP 이다.

    선형변환의 행렬표현에 의하여 다음이 성립한다.

    L⁡A(v1)=Av1=λv1 \operatorname{L}_{A}(v_1) = Av_1 = \lambda v_1
    L⁡A(v2)=Av2=∑i=1nai2vi \operatorname{L}_{A}(v _{2}) = Av _{2} = \sum_{i=1}^{n} a _{i2}v_i
    ⋮ \vdots
    L⁡A(vn)=Avn=∑i=1nai,nvi \operatorname{L}_{A}(v _{n}) = Av _{n} = \sum_{i=1}^{n} a _{i,n}v_i
    ⟹[L⁡A]γ=(λuOB)⟹[L⁡A]γ−tI=(λ−tuOB−tI) \implies [\operatorname{L}_{A}]_{\gamma } = \begin{pmatrix} \lambda & u\\ O & B \\ \end{pmatrix} \implies [\operatorname{L}_{A}]_{\gamma } - tI = \begin{pmatrix} \lambda -t & u\\ O & B - tI \\ \end{pmatrix}

    문제 4.3-21 에 의하여 다음이 성립한다.

    det⁡([L⁡A]γ−tI)=(λ−t)det⁡(B−tI) \det([\operatorname{L}_{A}]_{\gamma } - tI) = (\lambda - t) \det(B - tI)

    AA 의 특성다항식이 완전히 인수분해되는데 [L⁡A]γ[\operatorname{L}_{A}]_{\gamma } 는 AA 와 닮은 행렬이므로 문제 5.1-13 에 의하여 [L⁡A]γ[\operatorname{L}_{A}]_{\gamma } 의 특성다항식은 완전히 인수분해된다. 따라서 det⁡(B−tI)\det(B-tI) 도 완전히 인수분해된다. BB 는 n−1×n−1n -1 \times n-1 행렬이므로 귀납법의 가정에 의하여 가역행렬 QQ 에 대하여 U=Q−1BQU = Q ^{-1}BQ 인 상삼각행렬이 존재한다.

    R=(1O′OQ),R−1=(1O′OQ−1)R = \begin{pmatrix} 1&O'\\ O&Q\\ \end{pmatrix}, R ^{-1} = \begin{pmatrix} 1&O'\\ O&Q ^{-1}\\ \end{pmatrix} 로 두고 M=PRM = PR 로 두면 다음이 성립한다.

    M−1AM=R−1(P−1AP)R=(1O′OQ−1)(λuOB)(1O′OQ)=(λuQOU)=U′ \begin{align}\begin{split} M ^{-1}AM &= R ^{-1}(P ^{-1}AP)R \\ &= \begin{pmatrix} 1&O'\\ O&Q ^{-1}\\ \end{pmatrix}\begin{pmatrix} \lambda & u\\ O&B\\ \end{pmatrix} \begin{pmatrix} 1&O'\\ O&Q\\ \end{pmatrix}\\ &= \begin{pmatrix} \lambda &uQ\\ O&U \\ \end{pmatrix}= U' \end{split}\end{align} \tag*{}

    즉, AA 가 상삼각행렬 U′U' 와 닮음이니 모든 증명이 끝났다. ■

    2:

    V\mathbf{V} 의 순서기저 γ={x1,x2,…,xn}\gamma = \{x_1, x_2, \dots, x_n\} 에 대하여 A=[T⁡]γA = [\operatorname{T}]_{\gamma } 로 두자. 정리의 가정에 의하여 T⁡\operatorname{T} 의 특성다항식은 완전히 인수분해 되고 특성다항식의 정의에 의하여 AA 의 특성다항식도 완전히 인수분해된다. 따라서 이미 증명한 1) 에 의하여 AA 는 상삼각행렬 UU 와 닮은 행렬이다. 가역행렬 QQ 가 U=Q−1AQU = Q ^{-1}AQ 를 만족한다고 하면 j∈{1,…,n}j \in \{1,\dots,n\} 에 대하여 다음이 성립한다.

    yj=∑i=1nQijxi y_j = \sum_{i=1}^{n}Q _{ij}x_i

    문제 2.5-13 에 의하여 β={y1,y2,…,yn}\beta = \{y_1, y_2, \dots, y_n\} 는 V\mathbf{V} 의 기저이고 QQ 는 β\beta 좌표를 γ\gamma 좌표로 변환하는 좌표변환행렬이다. 정리 2.23 에 의하여 다음이 성립한다.

    ∴[T⁡]β=Q−1[T⁡]γQ=Q−1AQ=U■ \therefore [\operatorname{T}]_{\beta } = Q ^{-1}[\operatorname{T}]_{\gamma }Q = Q ^{-1}AQ = U \tag*{■}

Algebraic Multiplicity✔

대수적 중복도(algebraic multiplicity)

특성다항식이 f(t)f(t) 인 선형연산자(또는 행렬)의 고윳값 λ\lambda 에 대하여 (t−λ)k(t - \lambda )^{k} 가 f(t)f(t) 의 인수가 되도록 하는 가장 큰 자연수 kk 를 λ\lambda 의 대수적 중복도라고 한다.

  • 단순하게 중복도라고도 한다.

  • 예시

    A=(310034004)A = \begin{pmatrix} 3&1&0\\ 0&3&4\\ 0&0&4\\ \end{pmatrix} 의 특성다항식은 f(t)=−(t−3)2(t−4)f(t) = -(t-3)^{2}(t-4) 이므로 λ=3\lambda =3 의 중복도는 22, λ=4\lambda =4 의 중복도는 11 이다.

  • numpy

    A = np.array([[3,1,0], 
              [0,3,4],
              [0,0,4]])
eigval, eigvec = np.linalg.eig(A)
print(eigval)
print(eigvec)

    중복도에 따라 고윳값이 반복된다.

    [3. 3. 4.]
[[ 1.00000000e+00 -1.00000000e+00  6.96310624e-01]
 [ 0.00000000e+00  6.66133815e-16  6.96310624e-01]
 [ 0.00000000e+00  0.00000000e+00  1.74077656e-01]]

Eigenspace✔

선형연산자의 고유공간(eigenspace)

벡터공간 V\mathbf{V} 의 선형연산자 T⁡\operatorname{T} 와 고윳값 λ\lambda 에 대하여 다음 집합 Eλ\mathbf{E}_{\lambda} 를 고윳값 λ\lambda 에 대응하는 T⁡\operatorname{T} 의 고유공간이라 한다.

Eλ={x∈V:T⁡(x)=λx}=ker⁡(T⁡−λI⁡) \mathbf{E}_{\lambda} = \{x \in \mathbf{V} : \operatorname{T} (x) = \lambda x\} = \ker (\operatorname{T}-\lambda \operatorname{I} )

  • 즉, 고유공간은 특정 고윳값에 대응하는 모든 고유벡터를 모아둔 집합이다.

  • 고유공간은 고윳값에 대응하는 모든 벡터의 집합인데 정리 5.4 는 고윳값에 대응하는 모든 고유벡터를 찾는 방법을 알려준다. 따라서 고유공간은 정리 5.4 의 방법을 기반으로 정의된다.

    정리 5.4 는 행렬에 대하여 고윳값에 대응하는 모든 벡터를 구하는 방법을 서술하지만, 동형사상인 표준표현 ϕβ\phi _{\beta } 로 인하여 이 정리를 동일하게 선형연산자에서 사용할 수 있다. 다시 말해 정리 5.4 가 (A−λI)v=0(A - \lambda I)v=0 을 풀어서 고윳값에 대응하는 모든 고유벡터를 구하라고 말하는데, 이것은 동형사상인 표준표현에 의하여 영공간 ker⁡(T⁡−λI⁡V)\ker (\operatorname{T} - \lambda \operatorname{I} _{\mathbf{V}}) 을 구하는 것과 동치가 된다.

  • 이때 정리 5.4 와 달리 v≠0v \neq 0 라는 제한이 없으므로 정리 2.1 에 의하여 Eλ\mathbf{E}_{\lambda} 는 고윳값 λ\lambda 에 대응하는 T⁡\operatorname{T} 의 고유벡터와 영벡터로 이루어진 V\mathbf{V} 의 부분공간이다. 즉, Eλ\mathbf{E}_{\lambda} 의 차원은 고윳값 λ\lambda 에 대응하는 일차독립인 T⁡\operatorname{T} 의 고유벡터의 최대 개수이다.

행렬의 고유공간(eigenspace)

행렬 A∈Fn×nA \in \mathbf{F}^{n \times n} 의 고윳값 λ\lambda 벡터공간 Fn\mathbf{F}^{n} 의 선형연산자 L⁡A\operatorname{L}_{A} 에 대하여 다음 집합 Eλ\mathbf{E}_{\lambda} 를 고윳값 λ\lambda 에 대응하는 AA 의 고유공간이라 한다.

Eλ={x∈Fn:(A−λIn)x=0}=ker⁡(L⁡A−λI⁡Fn) \mathbf{E}_{\lambda} = \{x \in \mathbf{F}^{n} : (A - \lambda I_n)x = 0 \} = \ker (\operatorname{L}_{A}-\lambda \operatorname{I} _{\mathbf{F}^{n}})
  • 고유공간은 고윳값에 대응하는 모든 벡터의 집합인데 정리 5.4 는 고윳값에 대응하는 모든 고유벡터를 찾는 방법을 알려준다. 따라서 고유공간은 정리 5.4 의 방법을 기반으로 정의된다.

정리 5.7

유한차원 벡터공간 V\mathbf{V} 의 선형연산자 T⁡\operatorname{T} 와 중복도가 mm 인 T⁡\operatorname{T} 의 고윳값 λ\lambda 에 대하여 1≤dim⁡(Eλ)≤m1 \leq \dim (\mathbf{E}_{\lambda} )\leq m 이다.

  • 이 정리는 Eλ\mathbf{E}_{\lambda} 의 차원과 λ\lambda 의 중복도의 관계를 말해준다.

  • 증명

    정리 1.11 따름정리 에 의하여 Eλ\mathbf{E}_{\lambda} 의 순서기저 {v1,v2,…,vp}\{v_1, v_2, \dots, v_p\} 를 확장하여 V\mathbf{V} 의 순서기저 β={v1,v2,…,vp,vp+1,…,vn}\beta = \{v_1, v_2, \dots, v_p, v _{p+1}, \dots, v_n\} 를 만들 수 있다. 선형변환의 행렬표현 에 의하여 [T⁡]β=A[\operatorname{T} ]_{\beta }=A 을 11 열부터 nn 열까지는 다음과 같다.

    T⁡(v1)=a11v1=λ1v1 \operatorname{T} (v_1) = a _{11}v_1 = \lambda _1v_1
    ⋮ \vdots
    T⁡(vp)=appvp=λpvp \operatorname{T} (v_p) = a _{pp}v_p = \lambda _pv_p
    T⁡(vp+1)=∑i=1nai,p+1vp+1 \operatorname{T} (v _{p+1}) = \sum_{i=1}^{n} a _{i,p+1} v _{p+1}
    ⋮ \vdots
    T⁡(vn)=∑i=1nainvn \operatorname{T} (v _{n}) = \sum_{i=1}^{n} a _{in} v _{n}

    그러므로 어떤 행렬 B,CB, C 와 영행렬 OO 에 대하여 AA 는 다음과 같다.

    A=(λIpBOC) A = \begin{pmatrix} \lambda I_p&B\\ O&C\\ \end{pmatrix}

    문제 4.3-21 에 의하여 T⁡\operatorname{T} 의 특성다항식은 다음과 같다.

    f(t)=det⁡(A−tIn)=det⁡((λ−t)IpBOC−tIn−p)=det⁡((λ−t)Ip)det⁡(C−tIn−p)=(λ−t)pg(t) \begin{align}\begin{split} f(t)&= \det(A - tI_n) = \det \begin{pmatrix} (\lambda -t)I_p&B\\ O&C - tI _{n-p}\\ \end{pmatrix} \\ &= \det((\lambda -t)I_p) \det(C-tI _{n-p}) \\ &= (\lambda -t)^{p}g(t) \end{split}\end{align} \tag*{}

    따라서 λ\lambda 의 중복도 mm 에 대하여 p≤mp \leq m 이다. 그런데 dim⁡(Eλ)=p\dim (\mathbf{E}_{\lambda} ) = p 이므로 dim⁡(Eλ)≤m\dim (\mathbf{E}_{\lambda} ) \leq m 이다. ■

정리 5.8

유한차원 벡터공간 V\mathbf{V} 의 선형연산자 T⁡\operatorname{T} 에 대하여 T⁡\operatorname{T} 의 특성다항식이 완전히 인수분해되고 λ1,…,λk\lambda _1, \dots, \lambda _k 가 서로 다른 T⁡\operatorname{T} 의 고윳값일 때 다음이 성립한다.

  1. T⁡\operatorname{T} 가 대각화가능한 것과 모든 ii 에 대하여 λi\lambda _i 의 중복도가 dim⁡(Eλi)\dim (\mathbf{E}_{\lambda_i}) 인 것은 동치이다.

  2. T⁡\operatorname{T} 가 대각화가능하고 각각의 ii 에 대하여 βi\beta _{i} 가 Eλi\mathbf{E}_{\lambda_i} 의 순서기저일 때 β=⋃i=1kβi\beta = \displaystyle \bigcup_{i=1}^{k}\beta _{i} 는 T⁡\operatorname{T} 의 고유벡터로 이루어진 V\mathbf{V} 의 순서기저이다.

  • 순서기저 β=⋃i=1kβi\beta = \displaystyle \bigcup_{i=1}^{k}\beta _{i} 의 순서는 β1,…,βk\beta_1, \dots, \beta_k 의 벡터를 나열하는 순서 그대로이다.

  • 증명

    각각의 ii 에 대하여 mim_i 는 λi\lambda _i 의 중복도, di=dim⁡(Eλi)d_i = \dim (\mathbf{E}_{\lambda_i}), n=dim⁡(V)n = \dim (\mathbf{V} ) 라고 하자.

    T⁡\operatorname{T} 가 대각화가능함을 가정하면 T⁡\operatorname{T} 의 고유벡터로 이루어진 V\mathbf{V} 의 기저 β\beta 가 존재한다. 각 ii 에 대하여 βi=β∩Eλi\beta _i = \beta \cap \mathbf{E}_{\lambda_i} 의 기수를 ∣βi∣=ni|\beta _i| = n_i 라 하면 ni≤din_i \leq d_i 이다. 정리 1.10 따름정리 2 에 의하여 일차독립인 집합은 벡터공간의 차원보다 기수가 작기 때문이다. 또한 정리 5.7 에 의하여 di≤mid_i \leq m_i 이다.

    λi\lambda _i 에 대응하는 viv_i 들은 모두 서로 다르다. 만약 같은 vv 에 대하여 T⁡(v)=λiv=λjv\operatorname{T} (v) = \lambda _iv = \lambda _jv 가 성립하면 (λi−λj)v=0⟹λi=λj(\lambda _i-\lambda _j)v = 0 \implies \lambda _i = \lambda _j 가 된다. 그러므로 ∣β∣=n⟹∑i=1kni=n|\beta| = n \implies \sum_{i=1}^{k}n_i = n 이다.

    중복도는 그 정의에 의하여 모든 중복도의 합이 곧 특성다항식의 차수가 된다. [T⁡]β∈Fn×n[\operatorname{T}]_{\beta} \in \mathbf{F}^{n \times n} 의 특성다항식의 차수 nn 이므로 ∑i=1kmi=n\sum_{i=1}^{k}m_i = n 이다. 정리 5.5 는 βi\beta _i 가 일차독립 집합임을 말해준다.

    일차독립 집합은 정리 1.10 에 의하여 반드시 Eλi\mathbf{E}_{\lambda_i} 의 차원과 기수가 같거나 작다. 또한 정리 5.7 에 의하여 Eλi\mathbf{E}_{\lambda_i} 의 차원은 λi\lambda _i 의 중복도 mim_i 와 같거나 작다. 따라서 다음이 성립한다.

    n=∑i=1kni≤∑i=1kdi≤∑i=1kmi=n n = \sum_{i=1}^{k}n_i \leq \sum_{i=1}^{k}d_i \leq \sum_{i=1}^{k}m_i = n

    그러므로 ∑i=1k(mi−di)=0\displaystyle \sum_{i=1}^{k}(m_i - d_i) = 0 이다. 정리 5.7 에 의하여 mi−di≥0m_i - d_i \geq 0 이므로 각 ii 에 대하여 mi=dim_i = d_i 이다. ▲

    이제 모든 ii 에 대하여 mi=dim_i = d_i 를 가정하고, T⁡\operatorname{T} 가 대각화가능인 것과 2) 를 증명하자.

    각 ii 에 대하여 Eλi\mathbf{E}_{\lambda_i} 의 순서기저를 βi\beta _i 라 하고 β=⋃i=1kβi\beta = \bigcup_{i=1}^{k}\beta _i 를 정의하자. 그러면 정리 5.5 에 의해 β\beta 는 일차독립이다. 또한 ∣β∣=∑i=1kdi=∑i=1kmi=n|\beta | = \sum_{i=1}^{k}d_i = \sum_{i=1}^{k}m_i = n 이다. 중복도의 합이 특성다항식의 차수 nn 이 되기 때문이다. 정리 1.10 따름정리 2 에 의하여 β\beta 는 V\mathbf{V} 의 고유벡터로 이루어진 V\mathbf{V} 의 순서기저이다. 그러므로 정리 5.1 에 의하여 T⁡\operatorname{T} 는 대각화가능하다. ■

  • 예시

    R3\R ^{3} 의 선형연산자 T⁡\operatorname{T} 를 다음과 같이 정의하자.

    T⁡(a1a2a3)=(4a1+a32a1+3a2+2a3a1+4a3) \operatorname{T} \begin{pmatrix} a_1\\ a_2\\ a_3\\ \end{pmatrix} = \begin{pmatrix} 4a_1+a_3\\ 2a_1+3a_2+2a_3\\ a_1+4a_3\\ \end{pmatrix}

    표준순서기저 β\beta 에 대한 T⁡\operatorname{T} 의 행렬표현은 다음과 같다.

    [T⁡]β=(401232104) [\operatorname{T} ]_{\beta }=\begin{pmatrix} 4&0&1\\ 2&3&2\\ 1&0&4\\ \end{pmatrix}

    T⁡\operatorname{T} 의 특성다항식으로 모든 고윳값을 구해보자.

    det⁡([T⁡]β−tI)=det⁡(4−t0123−t2104−t)=−(t−5)(t−3)2 \det([\operatorname{T} ]_{\beta }-tI) = \det \begin{pmatrix} 4-t&0&1\\ 2&3-t&2\\ 1&0&4-t\\ \end{pmatrix} = -(t-5)(t-3)^{2}

    고윳값 λ1=5\lambda _1 = 5 와 λ2=3\lambda _2 = 3 중복도는 각각 1,21, 2 이므로 Eλ1\mathbf{E}_{\lambda_1} 와 Eλ2\mathbf{E}_{\lambda_2} 기저가 각각 1,21, 2 이면 T⁡\operatorname{T} 는 대각화 가능하다.

    Eλ1\mathbf{E}_{\lambda_1} 는 다음과 같다.

    Eλ1=ker⁡(T⁡−λ1I⁡)={(x1x2x3)∈R3:(−1012−2210−1)(x1x2x3)=(000)} \mathbf{E}_{\lambda_1} = \ker (\operatorname{T}-\lambda _1 \operatorname{I}) =\\ \Bigg \{\begin{pmatrix} x_1\\ x_2\\ x_3\\ \end{pmatrix}\in \R ^{3} : \begin{pmatrix} -1&0&1\\ 2&-2&2\\ 1&0&-1\\ \end{pmatrix}\begin{pmatrix} x_1\\ x_2\\ x_3\\ \end{pmatrix}=\begin{pmatrix} 0\\ 0\\ 0\\ \end{pmatrix}\Bigg \}

    따라서 Eλ1\mathbf{E}_{\lambda_1} 은 다음 연립방정식의 해공간 K=Eλ1\mathbf{K} = \mathbf{E}_{\lambda_1} 이다.

    −x1+x3=0 -x_1+x_3=0
    2x1−2x2+2x3=0 2x_1-2x_2+2x_3=0
    x1−x3=0 x_1-x_3=0

    계수행렬 AA 의 3행은 1행에 대하여 일차종속이므로 rank⁡(A)=2\operatorname{rank} (A) = 2 이다. 정리 3.8 에 의하여 dim⁡(K)=dim⁡(Eλ1)=3−rank⁡(A)=3−2=1\dim (\mathbf{K} ) = \dim (\mathbf{E}_{\lambda_1}) = 3 - \operatorname{rank} (A) = 3 - 2 = 1 이다. 기저를 구해보면 {(121)}\bigg \{\begin{pmatrix} 1\\ 2\\ 1\\ \end{pmatrix}\bigg \} 이다.

    같은 방법으로 dim⁡(Eλ2)=2\dim (\mathbf{E}_{\lambda_2}) = 2 를 알 수 있다. 기저를 구해보면 {(010),(−101)}\bigg \{\begin{pmatrix} 0\\ 1\\ 0\\ \end{pmatrix}, \begin{pmatrix} -1\\ 0\\ 1\\ \end{pmatrix}\bigg \} 이다.

    그러면 각 고윳값 λi\lambda _i 의 중복도가 고유공간 Eλi\mathbf{E}_{\lambda_i} 의 차원과 같으므로 정리의 1) 에 의하여 T⁡\operatorname{T} 는 대각화가능하다.

    T⁡\operatorname{T} 가 대각화가능이므로 Eλ1,Eλ2\mathbf{E}_{\lambda_1}, \mathbf{E}_{\lambda_2} 의 순서기저의 합집합 {(121),(010),(−101)}\bigg \{\begin{pmatrix} 1\\ 2\\ 1\\ \end{pmatrix}, \begin{pmatrix} 0\\ 1\\ 0\\ \end{pmatrix}, \begin{pmatrix} -1\\ 0\\ 1\\ \end{pmatrix}\bigg \} 은 정리의 2) 에 의하여 V\mathbf{V} 의 순서기저이다.

  • numpy

    A = np.array([[4,0,1], 
              [2,3,2],
              [1,0,4]])
eigval, eigvec = np.linalg.eig(A)
print(eigval)
print(eigvec)

    중복도에 따라 고윳값이 반복된다.

    [3. 5. 3.]
[[ 0.          0.40824829 -0.70710678]
 [ 1.          0.81649658  0.        ]
 [ 0.          0.40824829  0.70710678]]

    마찬가지로 각 고윳값에 같은 열에 고유벡터가 나온다.

Diagonalizable Determination✔

대각화 가능 판정법(Diagonalizable Determination)

nn차원 벡터공간 V\mathbf{V} 의 선형연산자 T⁡\operatorname{T} 가 대각화가능한 것과 다음 두 조건이 성립하는 것은 동치이다.

  1. T⁡\operatorname{T} 의 특성다항식이 완전히 인수분해된다.

  2. T⁡\operatorname{T} 의 고윳값 λ\lambda 의 중복도 mm 이 22 이상이면 mm 이 dim⁡(Eλ)=nullity⁡(T⁡−λI⁡)=n−rank⁡(T⁡−λI⁡)\dim(\mathbf{E}_{\lambda}) = \operatorname{nullity} (\operatorname{T} - \lambda \operatorname{I}) = n - \operatorname{rank} (\operatorname{T} - \lambda \operatorname{I} ) 와 같다.

  • 이 정리는 정리 5.8 의 첫번째 명제를 되풀어 말한 것 뿐이다.

  • 정사각행렬 AA 가 대각화가능한지 판정할 때도 이 방법을 사용한다. AA 의 대각화 가능성과 L⁡A\operatorname{L}_{A} 의 대각화 가능성이 동치이기 때문이다.

  • T⁡\operatorname{T} 가 대각화가능한 연산자이고 β1,…,βk\beta _1, \dots, \beta _k 가 T⁡\operatorname{T} 의 각각의 고유공간 Eλi\mathbf{E}_{\lambda_i} 의 순서기저이면 정리 5.8 에 의해 β=⋃βi\beta = \bigcup_{}^{}\beta _i 는 V\mathbf{V} 의 기저이고, [T⁡]β[\operatorname{T} ]_{\beta } 는 대각행렬이다.

    T⁡\operatorname{T} 가 대각화가능한지 판정하려면 V\mathbf{V} 의 기저 α\alpha 에 대한 B=[T⁡]αB = [\operatorname{T} ]_{\alpha} 를 다룬다. BB 의 특성다항식이 완전히 인수분해되면 중복도가 22 이상인 고윳값들이 n−rank⁡(B−λI)n - \operatorname{rank} (B - \lambda I) 와 같은지 확인한다. 모두 같으면 BB 와 T⁡\operatorname{T} 는 대각화 가능이다. (중복도가 11 인 고윳값들은 정리 5.7 에 의하여 자동으로 조건 2) 를 만족하게 된다.)

    T⁡\operatorname{T} 의 대각화가능이 확인되었다면 T⁡\operatorname{T} 의 고유벡터로 이루어진 V\mathbf{V} 의 기저 β\beta 를 찾아야 한다. 이를 위해 BB 의 각 고유공간에 대한 기저를 찾는다. 그러면 정리 5.8 에 의해 이 기저들의 합집합을 BB 의 고유벡터로 이루어진 Fn\mathbf{F} ^{n} 의 기저 γ\gamma 로 둘 수 있다.

    γ\gamma 의 각 벡터는 T⁡\operatorname{T} 의 고유벡터로 이루어진 α\alpha 에 대한 좌표벡터이다. 따라서 γ\gamma 를 통해 β\beta 를 구할 수 있다. 이 β\beta 를 통해 최종적으로 T⁡\operatorname{T} 를 [T⁡]β[\operatorname{T} ]_{\beta } 로 대각화할 수 있다.

  • 증명

    정리 5.6 은 T⁡\operatorname{T} 가 대각화가능이면 특성다항식이 완전히 인수분해됨을 말해준다. 그러나 완전히 인수분해된다고 해서 T⁡\operatorname{T} 가 대각화가능인 것은 아니다. 하지만 완전히 인수분해된다는 조건은 T⁡\operatorname{T} 가 대각화가능하기 위한 필요조건이다.

    T⁡\operatorname{T} 의 특성다항식이 완전히 인수분해되면 각각의 고윳값에 따른 중복도를 구할 수 있다. 이때 각 고윳값 λ\lambda 의 중복도가 dim⁡(Eλ)\dim (\mathbf{E}_{\lambda}) 와 같으면 정리 5.8 에 의하여 T⁡\operatorname{T} 는 대각화가능이 된다.

    중복도가 11 인 고윳값들은 정리 5.7 에 의하여 자동으로 조건 2) 를 만족하게 된다.

    dim⁡(Eλ)\dim (\mathbf{E}_{\lambda}) 는 특성다항식 T⁡−λI⁡V\operatorname{T} - \lambda \operatorname{I} _{\mathbf{V} } 의 영공간의 차원이다. 또한 정리 3.8 에 의하여 계수행렬 T⁡−λI⁡\operatorname{T} - \lambda \operatorname{I} 를 가지는 일차연립방정식의 해공간이기도 하다. ■

  • 예시

    행렬 A=(310030004)∈R3×3A = \begin{pmatrix} 3&1&0\\ 0&3&0\\ 0&0&4\\ \end{pmatrix} \in \R ^{3 \times 3} 의 대각화 가능성을 판정하자. det⁡(A−tI)=−(t−4)(t−3)2\det(A - tI) = -(t-4)(t-3)^{2} 이므로 λ1=4\lambda _1 = 4 는 조건 2) 를 자동으로 만족한다. λ2=3\lambda _2 = 3 에 대한 조건 2) 의 성립만 확인하면 T⁡\operatorname{T} 는 대각화가능하다.

    행렬 A−λ2I=(010000001)A - \lambda _2I = \begin{pmatrix} 0&1&0\\ 0&0&0\\ 0&0&1\\ \end{pmatrix} 의 랭크가 22 이므로 3−rank⁡(A−λ2I)=13 - \operatorname{rank} (A - \lambda _2I) = 1 은 λ2\lambda _2 의 중복도와 다르다. 따라서 AA 는 대각화 불가능이다.

  • 예시

    A = np.array([[3,1,0], 
              [0,3,0],
              [0,0,4]])
eigval, eigvec = np.linalg.eig(A)
print(eigval)
print(eigvec)

    중복도에 따라 고윳값이 반복된다.

    [3. 3. 4.]
[[ 1.00000000e+00 -1.00000000e+00  0.00000000e+00]
 [ 0.00000000e+00  6.66133815e-16  0.00000000e+00]
 [ 0.00000000e+00  0.00000000e+00  1.00000000e+00]]

    대각화가 불가능한데도 고유벡터가 출력되기는 한다. 실제로 6.66133815e-16 는 다음과 같은 비현실적인 수이다.

    0.000000000000000666133820.00000000000000066613382

    이런 수와 −1-1 이 선형 결합(linear combination)이라는 결과 자체가 직관적으로 말이 안된다.

  • 예시

    다음과 같은 벡터공간 P2(R)\mathbf{P}_{2}(\R) 의 선형연산자 T⁡\operatorname{T} 가 존재한다.

    T⁡(f(x))=f(1)+f′(0)x+(f′(0)+f′′(0))x2 \operatorname{T} (f(x)) = f(1) + f'(0)x + (f'(0)+f''(0))x ^{2}

    T⁡\operatorname{T} 의 대각화 가능성을 판정해보자. 표준순서기저 α\alpha 에 대하여 B=[T⁡]α=(111010012)B = [\operatorname{T} ]_{\alpha }= \begin{pmatrix} 1&1&1\\ 0&1&0\\ 0&1&2\\ \end{pmatrix} 이다. BB 와 T⁡\operatorname{T} 의 특성다항식은 −(t−1)2(t−2)-(t-1)^{2}(t-2) 으로써 완전히 인수분해된다. λ1=1\lambda _1=1 의 중복도는 22, λ2=2\lambda _2 = 2 의 중복도는 11 이다. λ1=1\lambda _1=1 이 조건 2) 를 만족하는지 살펴보자.

    3−rank⁡(B−λ1I)=3−rank⁡(011000011)=3−1=2 3 - \operatorname{rank} (B - \lambda _1I) = 3 - \operatorname{rank} \begin{pmatrix} 0&1&1\\ 0&0&0\\ 0&1&1\\ \end{pmatrix}=3-1=2

    따라서 T⁡\operatorname{T} 는 대각화 가능하다.

    이제 T⁡\operatorname{T} 를 대각화해보자. λ1=1\lambda _1 = 1 의 고유공간 Eλ1\mathbf{E}_{\lambda_1} 는 다음과 같다.

    Eλ1={(x1x2x3)∈R3:(011000011)(x1x2x3)=0} \mathbf{E}_{\lambda_1} = \bigg \{\begin{pmatrix} x_1\\ x_2\\ x_3\\ \end{pmatrix} \in \R ^{3} : \begin{pmatrix} 0&1&1\\ 0&0&0\\ 0&1&1\\ \end{pmatrix}\begin{pmatrix} x_1\\ x_2\\ x_3\\ \end{pmatrix} = 0\bigg \}

    이 고유공간의 기저는 γ1={(100),(0−11)}\gamma _1 = \bigg \{\begin{pmatrix} 1\\ 0\\ 0\\ \end{pmatrix}, \begin{pmatrix} 0\\ -1\\ 1\\ \end{pmatrix}\bigg \} 이다.

    Eλ2\mathbf{E}_{\lambda_2} 의 기저는 γ2={(101)}\gamma _2 = \bigg \{\begin{pmatrix} 1\\ 0\\ 1\\ \end{pmatrix}\bigg \} 이다. γ=γ1∪γ2={(100),(0−11),(101)}\gamma = \gamma _1 \cup \gamma _2 = \bigg \{\begin{pmatrix} 1\\ 0\\ 0\\ \end{pmatrix}, \begin{pmatrix} 0\\ -1\\ 1\\ \end{pmatrix}, \begin{pmatrix} 1\\ 0\\ 1\\ \end{pmatrix}\bigg \} 은 BB 의 고유벡터로 이루어진 R3\R ^{3} 의 순서기저이다. γ∈F3\gamma \in \mathbf{F} ^{3} 의 각 벡터는 β={1,−x+x2,1+x2}∈P2(R)\beta = \{1, -x+x ^{2}, 1+x ^{2}\} \in \mathbf{P}_{2}(\R) 의 α\alpha 에 대한 좌표벡터이다. β\beta 는 T⁡\operatorname{T} 의 고유벡터로 이루어진 P2(R)\mathbf{P}_{2}(\R) 의 순서기저이므로 T⁡\operatorname{T} 를 대각화해보면 다음과 같다.

    [T⁡]β=(100010002) [\operatorname{T} ]_{\beta } = \begin{pmatrix} 1&0&0\\ 0&1&0\\ 0&0&2\\ \end{pmatrix}

  • numpy

    A = np.array([[1,1,1], 
              [0,1,0],
              [0,1,2]])
eigval, eigvec = np.linalg.eig(A)
print(eigval)
print(eigvec)

    [1. 2. 1.]
[[ 1.          0.70710678  0.        ]
 [ 0.          0.          0.70710678]
 [ 0.          0.70710678 -0.70710678]]

    중복도에 따라 고윳값이 반복된다.

대각화 요약

  1. nn차원 벡터공간 V\mathbf{V} 의 선형연산자 T⁡\operatorname{T} 를 대각행렬 [T⁡]β[\operatorname{T}]_{\beta} 로 표현할 수 있는 기저 β\beta 가 존재하면 T⁡\operatorname{T} 를 대각화가능하다고 말한다.

  2. T⁡\operatorname{T} 를 대각화 할 수 있는 기저를 β={v1,v2,…,vn}\beta = \{v_1, v_2, \dots, v_n\} 로 두면 T⁡\operatorname{T} 를 대각행렬로 표현하는 과정에서 반드시 T⁡(vi)=λivi\operatorname{T}(v_i) = \lambda _iv_i 꼴의 결과가 나오게 된다.

    바로 이 형태 T⁡(v)=λv\operatorname{T}(v) = \lambda v 를 일반화하여 vv 를 고유벡터, λ\lambda 를 고윳값이라 정의한다.

  3. 그러면 T⁡\operatorname{T} 를 대각화할 수 있다는 것은 T⁡\operatorname{T} 의 고유벡터로 이루어진 V\mathbf{V} 의 기저가 존재한다는 것이 된다.

  4. 따라서 T⁡\operatorname{T} 를 대각화하고 싶다면 V\mathbf{V} 안에서 서로 일차독립인 T⁡\operatorname{T} 의 고유벡터들을 nn개 찾기만 하면 된다. 그러면 서로 일차독립인 T⁡\operatorname{T} 의 고유벡터 nn개를 어떻게 찾는가?

  5. (고윳값 구하기) 특성다항식의 근을 구하면 선형연산자가 지니는 모든 고윳값을 하나도 빠짐없이 알 수 있다. 선형연산자의 서로 다른 고윳값은 최대 nn개이다(정리 5.3). 만약 특성다항식의 근이 존재하지 않으면 고윳값도 존재하지 않으며 대각화 불가능하다.

  6. (고유벡터 구하기) 고유공간은 고윳값에 대응하는 모든 고유벡터들의 집합이며 V\mathbf{V} 의 부분공간이다. 따라서 고유공간의 기저를 구하면 고윳값에 대응하는 일차독립인 고유벡터들을 구할 수 있다.

  7. 각각의 고윳값에 대응하는 일차독립 집합들의 합집합은 일차독립이다(정리 5.8). 또한 고유공간의 차원은 항상 고윳값의 중복도와 같거나 작다(정리 5.7).

  8. 따라서 만약 특성다항식의 근이 nn개라면, 각 고유공간은 1차원이고 그것들의 기저를 모으면 선형연산자 T⁡\operatorname{T} 를 대각화하는 V\mathbf{V} 의 기저를 얻는다. 즉, 대각화 가능하다.(정리 5.5 따름정리)

    만약 특성다항식의 근이 nn개 보다 작다면, 어떤 고윳값의 중복도가 2 이상이라는 것이다. 그러한 고윳값의 고유공간의 차원이 중복도보다 작으면, 아무리 모든 고유공간의 기저를 모아도 일차독립인 고유벡터들의 개수가 nn 보다 작을 수밖에 없고, 대각화 불가능하다. 즉, 어떤 고유공간이 너무 작으면 대각화 불가능하다.

    따라서 이 경우 T⁡\operatorname{T} 가 대각화 가능하려면 중복도가 2 이상인 고윳값의 고유공간의 차원이 반드시 중복도와 같아야 한다. 그러면 대각화 가능하고, 고유공간의 기저를 모으면 T⁡\operatorname{T} 를 대각화하는 V\mathbf{V} 의 기저를 얻는다.

    즉, T⁡\operatorname{T} 의 고유공간의 기저의 합집합이 V\mathbf{V} 의 기저가 되면 T⁡\operatorname{T} 는 대각화 가능하다. 이 과정이 어떤 이유에서든 실패하면 T⁡\operatorname{T} 는 대각화 불가능하다.

  9. 그러나 T⁡\operatorname{T} 를 대각화할 수 없는 경우라고 해도 아직 희망은 남아있다. 물론 대각행렬표현이 T⁡\operatorname{T} 를 가장 단순하게 표현할 수 있는 형태이긴 하지만, 이 형태를 대체할 수 있는 여러가지 행렬표현 형태들이 존재한다. 이 행렬표현을 표준형이라 한다.

    대각화 불가능한 T⁡\operatorname{T} 의 특성다항식이 완전히 인수분해되는 경우 조르당 표준형으로 T⁡\operatorname{T} 를 행렬표현하면 된다.

    대각화 불가능한 T⁡\operatorname{T} 의 특성다항식이 완전히 인수분해되지 않으면 유리 표준형으로 T⁡\operatorname{T} 를 행렬표현한다.

Matrix Limits✔

복소수 수열의 극한(limite a sequence of complex number)

복소수 수열의 극한 {zm:m=1,2,…}\{z_m : m = 1, 2, \dots\} 은 실수부와 허수부 각각의 극한으로 정의하여 실수 rm,smr_m, s_m 에 대하여 lim⁡m→∞rm\displaystyle \lim_{m \to \infty} r_m 과 lim⁡m→∞sm\displaystyle \lim_{m \to \infty} s_m 가 존재할 때 zm=rm+ismz_m = r_m + is_m 이라 하면 다음이 성립한다.

lim⁡m→∞zm=lim⁡m→∞rm+ilim⁡m→∞sm \lim_{m \to \infty} z_m = \lim_{m \to \infty} r_m + i \lim_{m \to \infty} s_m

행렬의 극한(limit of matrix)

행렬 L∈Cn×pL \in \Bbb{C}^{n \times p} 와 행렬열 A1,A2,⋯∈Cn×pA_1, A_2, \dots \in \Bbb{C}^{n \times p} 에 대하여 임의의 1≤i≤n1 \leq i \leq n 과 1≤j≤p1 \leq j \leq p 에 대하여 lim⁡m→∞(Am)ij=Lij\displaystyle \lim_{m \to \infty} (A_m) _{ij} = L _{ij} 일 때 행렬열 A1,A2,…A_1, A_2, \dots 이 행렬 LL 로 수렴한다고 한다.

이때 행렬 LL 을 행렬열 A1,A2,…A_1, A_2, \dots 의 극한이라 하며, lim⁡m→∞Am=L\displaystyle \lim_{m \to \infty} A_m = L 라고 표기한다.

  • 예시

    Am=(1m3(i/2)m2)⟹lim⁡m→∞Am=(0302) A_m = \begin{pmatrix} \frac{1}{m} & 3\\ (i/2) ^{m} & 2\\ \end{pmatrix} \implies \lim_{m \to \infty} A_m = \begin{pmatrix} 0&3\\ 0&2\\ \end{pmatrix}

정리 5.11

행렬열 A1,A2,⋯∈Cn×pA_1, A_2, \dots \in \Bbb{C}^{n \times p} 이 행렬 LL 로 수렴할 때 임의의 P∈Cr×nP \in \Bbb{C} ^{r \times n} 와 Q∈Cp×sQ \in \Bbb{C} ^{p \times s} 에 대하여 다음이 성립한다.

lim⁡m→∞PAm=PL \lim_{m \to \infty} PA_m = PL
lim⁡m→∞AmQ=LQ \lim_{m \to \infty} A_mQ = LQ

  • 실수열 극한에서 lim⁡m→∞cam=clim⁡m→∞am\displaystyle \lim_{m \to \infty} ca_m = c \lim_{m \to \infty} a_m 이 성립하는 성질과 비슷하다.

  • 증명

    임의의 1≤i≤r,1≤j≤p1 \leq i \leq r, 1 \leq j \leq p 에 대하여 다음이 성립한다.

    lim⁡m→∞(PAm)ij=lim⁡m→∞∑k=1nPik(Am)kj \lim_{m \to \infty} (PA_m) _{ij} = \lim_{m \to \infty} \sum_{k=1}^{n}P _{ik}(A_m) _{kj}
    =∑k=1nPiklim⁡m→∞(Am)kj=∑k=1nPikLkj=(PL)ij = \sum_{k=1}^{n}P _{ik}\lim_{m \to \infty} (A_m) _{kj} = \sum_{k=1}^{n}P _{ik}L _{kj} = (PL) _{ij}

    즉, lim⁡m→∞PAm=PL\displaystyle \lim_{m \to \infty} PA_m = PL 이다. 같은 방식으로 두번째 명제도 증명 가능하다. ■

정리 5.11 따름정리

lim⁡m→∞Am=L\displaystyle \lim_{m \to \infty} A ^{m} = L 인 행렬 A∈Cn×nA \in \Bbb{C} ^{n \times n} 와 임의의 가역행렬 Q∈Cn×nQ \in \Bbb{C} ^{n \times n} 에 대하여 다음이 성립한다.

lim⁡m→∞(QAQ−1)m=QLQ−1 \lim_{m \to \infty} (QAQ ^{-1}) ^{m} = QLQ ^{-1}

  • 증명

    (QAQ−1)m=(QAQ−1)(QAQ−1)…(QAQ−1)=QAmQ−1(QAQ ^{-1})^{m} = (QAQ ^{-1})(QAQ ^{-1}) \dots (QAQ ^{-1}) = QA ^{m}Q ^{-1} 와 정리 5.11 에 의하여 다음이 성립한다.

    lim⁡m→∞(QAQ−1)m=lim⁡m→∞QAmQ−1=Q(lim⁡m→∞Am)Q−1=QLQ−1■ \lim_{m \to \infty} (QAQ ^{-1})^{m} = \lim_{m \to \infty} QA ^{m}Q ^{-1} = Q \bigg (\lim_{m \to \infty} A ^{m}\bigg )Q ^{-1} = QLQ ^{-1} \tag*{■}

정리 5.12

집합 S={λ∈C:∣λ∣<1∨λ=1}S = \{\lambda \in \Bbb{C}: |\lambda | < 1 \lor \lambda = 1\} 과 정사각행렬 A∈Cn×nA \in \Bbb{C} ^{n \times n} 에 대하여 lim⁡m→∞Am\displaystyle \lim_{m \to \infty} A ^{m} 이 존재하는 것과 다음 두 명제가 성립하는 것은 동치이다.

  1. AA 의 모든 고윳값이 SS 의 원소이다.

  2. 11 이 AA 의 고윳값이면 11 에 대응하는 고유공간의 차원은 고윳값 11 의 중복도와 같다.

  • 증명

    1) 이 필요한 조건임을 증명하자. AA 의 고윳값 λ\lambda 가 λ∉S\lambda \not\in S 라고 하고 λ\lambda 에 대응하는 고유벡터를 vv 라고 하자. 정리 5.11 에 의하여 lim⁡m→∞(Amv)=(lim⁡m→∞Am)v=Lv\displaystyle \lim_{m \to \infty} (A ^{m}v) = \bigg (\lim_{m \to \infty} A ^{m}\bigg )v = Lv 이다. 그런데 lim⁡m→∞λm\displaystyle \lim_{m \to \infty} \lambda ^{m} 이 발산하므로 lim⁡m→∞(Amv)=lim⁡m→∞(λmv)\displaystyle \lim_{m \to \infty} (A ^{m}v) = \lim_{m \to \infty} (\lambda ^{m}v) 도 발산한다. 이는 모순이다. 따라서 1) 이 성립해야만 한다. ▲

    2) 가 필요한 조건임을 증명하는 것은 조르당 표준형을 사용하는 방법(문제 7.2-19)이나 슈어의 정리를 사용한다.

정리 5.13

집합 S={λ∈C:∣λ∣<1∨λ=1}S = \{\lambda \in \Bbb{C}: |\lambda | < 1 \lor \lambda = 1\} 과 정사각행렬 A∈Cn×nA \in \Bbb{C} ^{n \times n} 에 대하여 lim⁡m→∞Am\displaystyle \lim_{m \to \infty} A ^{m} 이 존재하는 것과 다음 두 명제가 성립하는 것은 동치이다.

  1. AA 의 모든 고윳값이 SS 의 원소이다.

  2. AA 가 대각화 가능하다.

  • 행렬의 극한과 관련된 문제들에 대부분 대각화가능한 행렬이 나오는데, 행렬이 대각화 가능하면 정리 5.12 의 조건 2) 가 자동으로 만족된다. 이 경우 정리 5.12 를 단순화시킨 이 정리를 사용한다.

  • 증명

    2) 가 성립하면, 즉 AA 가 대각화 가능하면 Q−1AQ=DQ ^{-1}AQ = D 가 대각행렬이 되게 하는 가역행렬 QQ 가 존재한다. D=diag⁡(λ1,λ2,…,λn)D = \operatorname{diag} (\lambda _1, \lambda _2, \dots, \lambda _n) 에 대하여 1) 이 성립하면 λi=1\lambda _i = 1 또는 ∣λi∣<1|\lambda _i| < 1 이다. 따라서 다음이 성립한다.

    lim⁡m→∞λim={1(λi=1)0( else ) \lim_{m \to \infty} \lambda _i ^{m} = \begin{cases} 1 &(\lambda _i = 1)\\ 0 &(\text{ else })\\ \end{cases}

    따라서 행렬 Dm=diag⁡(λ1m,…,λnm)D ^{m} = \operatorname{diag} (\lambda _1 ^{m}, \dots, \lambda _n ^{m}) 에 대하여 lim⁡m→∞Dm=L\displaystyle \lim_{m \to \infty} D ^{m} = L 이다. 정리 5.11 따름정리에 의하여 다음이 성립한다.

    lim⁡m→∞Am=lim⁡m→∞(QDQ−1)m=QLQ−1 \lim_{m \to \infty} A ^{m} = \lim_{m \to \infty} (QDQ ^{-1}) ^{m} = QLQ ^{-1}

    즉, lim⁡m→∞Am\displaystyle \lim_{m \to \infty} A ^{m} 이 존재한다. ■

  • 위 증명과정에서 AmA ^{m} 의 극한을 구하는 과정은 행렬의 거듭제곱 극한을 구할 때 자주 사용된다.

  • 예시

    다음 행렬 AA 에 대하여 lim⁡m→∞Am\displaystyle \lim_{m \to \infty} A ^{m} 를 구해보자.

    A=14(7−9−153733−9−11) A = \frac{1}{4} \begin{pmatrix} 7&-9&-15\\ 3&7&3\\ 3&-9&-11\\ \end{pmatrix}

    AA 를 대각화하면 다음과 같은 고유공간의 기저를 열로 가지는 행렬 QQ 와 대각행렬 DD 에 대하여 Q−1AQ=DQ ^{-1}AQ = D 가 성립한다.

    Q=(13−1−3−2123−1),D=(1000−1/20001/4) Q = \begin{pmatrix} 1&3&-1\\ -3&-2&1\\ 2&3&-1\\ \end{pmatrix}, D = \begin{pmatrix} 1&0&0\\ 0&-1/2&0\\ 0&0&1/4\\ \end{pmatrix}

    그러면 AmA ^{m} 의 극한을 다음과 같이 쉽게 계산할 수 있다.

    lim⁡m→∞Am=lim⁡m→∞(QDQ−1)m=lim⁡m→∞QDmQ−1=Q(lim⁡m→∞Dm)Q−1 \lim_{m \to \infty} A ^{m} = \lim_{m \to \infty} (QDQ ^{-1}) ^{m} = \lim_{m \to \infty} QD ^{m}Q ^{-1} = Q \bigg (\lim_{m \to \infty} D ^{m}\bigg )Q ^{-1}
    =(13−1−3−2123−1)lim⁡m→∞(1000(−1/2)m000(1/4)m)(−101−112−537) = \begin{pmatrix} 1&3&-1\\ -3&-2&1\\ 2&3&-1\\ \end{pmatrix}\lim_{m \to \infty} \begin{pmatrix} 1&0&0\\ 0&(-1/2)^m&0\\ 0&0&(1/4)^m\\ \end{pmatrix}\begin{pmatrix} -1&0&1\\ -1&1&2\\ -5&3&7\\ \end{pmatrix}
    =(13−1−3−2123−1)(100000000)(−101−112−537)=(−10130−3−202) = \begin{pmatrix} 1&3&-1\\ -3&-2&1\\ 2&3&-1\\ \end{pmatrix} \begin{pmatrix} 1&0&0\\ 0&0&0\\ 0&0&0\\ \end{pmatrix} \begin{pmatrix} -1&0&1\\ -1&1&2\\ -5&3&7\\ \end{pmatrix} = \begin{pmatrix} -1&0&1\\ 3&0&-3\\ -2&0&2\\ \end{pmatrix}

추이행렬(transition matrix, 확률행렬, stochastic matrix)

음이 아닌 성분을 가지고 각 열의 합이 11 인 행렬이다.

  • n×nn \times n 추이행렬 MM 의 각 행과 열은 nn가지 상태를 뜻하고, MijM _{ij} 성분은 한 단계에 의하여 상태 jj 가 상태 ii 로 바뀔 확률을 뜻한다.

    또한 (Mm)ij(M ^{m})_{ij} 성분은 mm단계 후에 상태 jj 가 상태 ii 로 바뀔 확률이다.

  • 예시

    다음 행렬 AA 의 성분이 도시나 교외에 거주하는 사람이 1년 후 도시나 교외에 거주할 확률을 나타낸다.

    A=(0.90.020.10.98) A = \begin{pmatrix} 0.9&0.02\\ 0.1&0.98\\ \end{pmatrix}

    1행은 내년에 도시에 거주할 확률, 2행은 내년에 교외에 거주할 확률을 나타내고, 1열은 현재 도시에 거주하는 사람, 2열은 현재 교외에 거주하는 사람을 나타낸다. 가령 현재 도시에 거주하는 사람이 내년에 교외에서 거주할 확률은 0.1 이다.

    A21A _{21} 은 한 단계(1년) 후에 도시에 거주하는 상태가 교외에 거주하는 상태로 바뀔 확률이다. 그러면 2년 후 도시에서 교외로 바뀔 확률은 어떻게 될까? 이 확률은 첫 해에 도시에 머무르고(0.9) 두번째 해에 교외로 이동하는 확률(0.1)과 첫 해에 교외로 이동하고(0.1) 두번째 해에 움직이지 않을(0.98) 확률의 합이다. 즉, 0.9×0.1+0.1×0.98=0.1880.9 \times 0.1 + 0.1 \times 0.98 = 0.188 이다. 그런데 이 계산 과정과 결과는 (A2)21(A ^{2}) _{21} 을 구하는 것과 같다.

확률벡터(probability vector)

음이 아닌 성분을 갖고 성분의 합이 11 인 벡터이다.

  • 예시

    추이행렬의 예시를 그대로 생각하자.

    이제 2000년도에 인구의 70% 가 도시에 거주하고 30% 가 교외에 머문다고 하자. 이를 열벡터로 나타내면 다음과 같다.

    P=(0.70.3) P = \begin{pmatrix} 0.7\\ 0.3\\ \end{pmatrix}

    벡터 AP=(0.6360.364)AP = \begin{pmatrix} 0.636\\ 0.364\\ \end{pmatrix} 의 첫번째 성분은 0.9×0.7+0.02×0.30.9 \times 0.7 + 0.02 \times 0.3 의 결과이다. 0.9×0.70.9 \times 0.7 은 2000년도 도시 거주자가 1년 후에도 도시에 머무는 비율이고, 0.02×0.30.02 \times 0.3 은 2000년도 교외 거주자가 1년 후에는 도시에 머무는 비율이다. 마찬가지로 두번째 성분은 1년 후 교외 거주자의 비율이 된다.

    같은 논리로 A2P=(0.579680.42032)A ^{2}P = \begin{pmatrix} 0.57968\\ 0.42032\\ \end{pmatrix} 는 2년 후의 도시 거주자, 교외 거주자의 비율이 된다. 일반적으로 AmPA ^{m}P 은 mm년 후 도시 거주자와 교외 거주자의 비율을 보여준다.

    인구 이동 경향의 확률이 영원히 유지된다고 가정하면 궁극적으로 도시와 교외의 인구 비율은 어떻게 될까? AA 가 대각화 가능하다는 것은 쉽게 보일 수 있다. Q−1AQ=DQ ^{-1}AQ = D 가 대각행렬이 되게 하는 가역행렬 QQ 와 DD 는 다음과 같다.

    Q=16(1−151),D=(1000.88) Q = \frac{1}{6}\begin{pmatrix} 1&-1\\ 5&1\\ \end{pmatrix}, D = \begin{pmatrix} 1&0\\ 0&0.88\\ \end{pmatrix}

    따라서 AmA ^{m} 의 극한은 다음과 같다.

    lim⁡m→∞Am=lim⁡m→∞QDmQ−1=Q(1000)Q−1=16(1155)=L \lim_{m \to \infty} A ^{m} = \lim_{m \to \infty} QD ^{m}Q ^{-1} = Q \begin{pmatrix} 1&0\\ 0&0\\ \end{pmatrix}Q ^{-1} = \frac{1}{6}\begin{pmatrix} 1&1\\ 5&5\\ \end{pmatrix} = L

    따라서 LP=(1/65/6)LP = \begin{pmatrix} 1/6\\ 5/6\\ \end{pmatrix} 이다. 즉, 인구 이동 경향성이 유지된다면 인구의 ⅙ 이 도시에 살게 되고 ⅚ 이 교외에 살게 된다는 결론을 얻는다.

  • 주목할만한 점은 A(LP)=LPA(LP) = LP 가 성립하므로 LPLP 는 확률벡터이자 고윳값 11 에 대응하는 AA 의 고유벡터이다. 고윳값 11 에 대응하는 고유공간은 11차원이므로 이 벡터는 유일하다.

    또한 LPLP 는 처음 확률벡터 PP 를 어떻게 선택하든 관계 없다. 가령 초기에(2000년도) 모든 사람이 도시에 거주하고 있어도 결과는 똑같다.

정리 5.14

행렬 M∈R≥0n×nM \in \R _{\geq 0} ^{n \times n} 과 열벡터 v∈R≥0nv \in \R ^{n} _{\geq 0} 와 각 성분이 11 인 열벡터 u∈Rnu \in \R ^{n} 에 대하여 다음이 성립한다.

  1. MM 이 추이행렬인 것과 u⊤M=u⊤u ^{\top}M = u ^{\top} 인 것은 동치이다.

  2. vv 가 확률벡터인 것과 u⊤v=(1)u ^{\top}v = (1) 인 것은 동치이다.
  • 증명

정리 5.14 따름정리

  1. 두 n×nn \times n 추이행렬의 곱은 n×nn \times n 추이행렬이다. 추이행렬의 거듭제곱은 추이행렬이다.

  2. 추이행렬과 확률벡터의 곱은 확률벡터이다.
  • 증명

확률 과정(stochastic process)

시간이 지나면서 한 상태가 다른 상태로 바뀌는 과정을 확률 과정(stochastic process)이라 한다.

  • 이렇게 도시-교외 문제를 살펴보았는데, 시간이 지나면서 한 상태가 다른 상태로 바뀌는 과정을 확률 과정이라 한다. 각 상태가 바뀌는 과정을 확률로 표현하는 것이다. 이 확률은 1) 확률을 묻는 시점의 상태, 2) 확률을 묻는 시점의 시간, 3) 대상의 과거와 지금을 종합한 상태의 일부 또는 전부, 4) 다른 대상의 과거와 지금을 종합한 상태의 일부 또는 전부에 영향을 받는다.

    대상이 한 상태에서 다른 상태로 바뀌는 확률이 오직 두 상태에 의하여 결정될 때 이 확률 과정을 마르코프 과정(Markov process)라고 한다. 가능한 상태의 경우의 수가 유한한 마르코프 과정을 마르코프 연쇄(Markov chain)이라 한다.

    도시-교외 문제는 두 상태로 이루어진 마르코프 연쇄이다. 그러나 마르코프 연쇄는 실제 현실을 정확하게 반영하지는 못한다. 왜냐하면 시간이 흐르면서 확률도 변하기 때문이다.

Direct sum✔

집합의 덧셈, 합(sum)

벡터공간 V\mathbf{V} 의 부분공간 W1,W2,…,Wk\mathbf{W} _1, \mathbf{W} _2, \dots, \mathbf{W} _k 에 대하여 다음 집합을 부분공간의 합이라 한다.

∑i=1kWi:={∑i=1kvi:vi∈Wi} \sum_{i=1}^{k}\mathbf{W} _i := \bigg \{\sum_{i=1}^{k}v_i : v_i \in \mathbf{W} _i \bigg \}

  • 예시

    R3\R ^{3} 에서 xyxy평면을 나타내는 부분공간 W1\mathbf{W} _1, yzyz평면을 나타내는 부분공간 W2\mathbf{W} _2 를 잡자. (a,0,0)∈W1,(0,b,c)∈W2(a, 0, 0) \in \mathbf{W} _1, (0, b, c) \in \mathbf{W} _2 에 대하여 다음이 성립한다.

    (a,b,c)=(a,0,0)+(0,b,c)∈R3 (a, b, c) = (a, 0, 0) + (0, b, c) \in \R ^{3}

    따라서 R3=W1+W2\R ^{3} = \mathbf{W} _1 + \mathbf{W} _2 이다.

직합(direct sum)

벡터공간 V\mathbf{V} 의 부분공간 W1,W2,…,Wk\mathbf{W} _1, \mathbf{W} _2, \dots, \mathbf{W} _k 를 잡자. 다음이 성립하면 V\mathbf{V} 를 W1,W2,…,Wk\mathbf{W} _1, \mathbf{W} _2, \dots, \mathbf{W} _k 의 직합이라 하고, V=W1⊕W2⊕⋯⊕Wk=⨁i=1kWi\mathbf{V} = \mathbf{W} _1 \oplus \mathbf{W} _2 \oplus \dots \oplus \mathbf{W} _k = \bigoplus_{i=1}^{k}\mathbf{W} _i 와 같이 표기한다.

  1. V=∑i=1kWi\displaystyle \mathbf{V} = \sum_{i=1}^{k}\mathbf{W} _i

  2. Wj∩∑i≠jWi={0}(1≤j≤k)\displaystyle \mathbf{W} _j \cap \sum_{i \neq j}^{}\mathbf{W} _i = \{0\} \qquad (1 \leq j \leq k)

  • 직합은 V\mathbf{V} 를 간단한 부분공간으로 분해하는 방법을 제공한다. 이는 V\mathbf{V} 의 선형연산자 T⁡\operatorname{T} 가 V\mathbf{V} 에 어떻게 작용하는지 파악할 수 있게 해준다.

    또한 직합은 대각화 불가능한 선형연산자를 다룰 때 유용하게 사용된다.

  • 예시

    R5\R ^{5} 의 W={(x1,x2,x3,x4,x5):x5=0},W1={(a,b,c,0,0):a,b,c∈R},W2={(0,0,0,d,0):d∈R}\mathbf{W} = \{(x_1, x_2, x_3, x_4, x_5) : x_5 = 0\}, \mathbf{W}_1 = \{(a, b, c, 0, 0) : a, b, c \in \R \}, \mathbf{W}_2 = \{(0, 0, 0, d, 0) : d \in \R \} 에 대하여 다음이 성립한다.

    (a,b,c,d,0)=(a,b,c,0,0)+(0,0,0,d,0)∈W1+W2 (a, b, c, d, 0) = (a, b, c, 0, 0) + (0, 0, 0, d, 0) \in \mathbf{W} _1 + \mathbf{W} 2

    따라서 W=∑i=12Wi\mathbf{W} = \sum_{i=1}^{2}\mathbf{W} _i 이다.

    또한 W1∩W2={0}\mathbf{W} _1 \cap \mathbf{W} _2 = \{0\} 이다. 따라서 W1⊕W2=W\displaystyle \mathbf{W} _1 \oplus \mathbf{W} _2 = \mathbf{W} 이다.

Properties of direct sum✔

정리 5.9

유한차원 벡터공간 V\mathbf{V} 의 부분공간 W1,W2,…,Wk\mathbf{W} _1, \mathbf{W} _2, \dots, \mathbf{W} _k 와 i∈{1,…,k}i \in \{1, \dots, k\} 에 대하여 다음은 동치이다.

  1. V=⨁i=1kWi\displaystyle \mathbf{V} = \bigoplus_{i=1}^{k}\mathbf{W} _i

  2. V=∑i=1kWi\displaystyle \mathbf{V} = \sum_{i=1}^{k}\mathbf{W} _i 이고 vi∈Wiv_i \in \mathbf{W} _i 에 대하여 ∑i=1kvi=0\displaystyle \sum_{i=1}^{k}v_i = 0 이면 vi=0v_i = 0 이다.

  3. v∈Vv \in \mathbf{V} 에 대하여 v=∑i=1kviv = \displaystyle \sum_{i=1}^{k}v_i 를 만족하는 vi∈Wiv_i \in \mathbf{W} _i 가 유일하게 존재한다.

  4. Wi\mathbf{W} _i 의 순서기저 γi\gamma _i 에 대하여 ⋃i=1kγi\displaystyle \bigcup_{i=1}^{k}\gamma _i 는 V\mathbf{V} 의 순서기저이다.

  5. ⋃i=1kγi\displaystyle \bigcup_{i=1}^{k}\gamma _i 가 V\mathbf{V} 의 순서기저가 되게 하는 Wi\mathbf{W} _i 의 순서기저 γi\gamma _i 가 존재한다.

  • 이 정리는 직합의 정의와 동치인 명제들을 말해준다.

  • 1 에서 2 를 도출하는 증명

    직합의 정의에 의하여 V=∑i=1kWi\mathbf{V} = \displaystyle \sum_{i=1}^{k}\mathbf{W} _i 이고 가정에 의하여 vi∈Wiv_i \in \mathbf{W} _i 에 대하여 ∑i=1kvi=0\displaystyle \sum_{i=1}^{k}v_i = 0 이다. 임의의 jj 에 대하여 합의 정의에 의하여 −vj=∑i≠jvi∈∑i≠jWi-v_j = \displaystyle \sum_{i\neq j}^{} v_i \in \displaystyle \sum_{i\neq j}^{}\mathbf{W} _i 이다. 부분공간은 스칼라곱에 대하여 닫혀있으므로 −vj∈Wj-v_j \in \mathbf{W} _j 이고, 직합의 정의에 의하여 −vj∈Wj∩∑i≠jWi={0}-v_j \in \mathbf{W} _j \cap \displaystyle \sum_{i\neq j}^{}\mathbf{W} _i = \{0\} 이다. 이는 vj=0v_j = 0 임을 뜻한다. ■

  • 2 에서 3 를 도출하는 증명

    2) 는 부분공간의 합이 곧 원래의 벡터공간이 됨을 말하므로 v∈Vv \in \mathbf{V} 와 vi∈Wiv_i \in \mathbf{W} _i 에 대하여 v=v1+v2+⋯+vkv = v_1 + v_2 + \dots + v_k 인 벡터 v1,v2,…,vkv_1, v_2, \dots, v_k 가 존재한다.

    존재성 증명이 되었으니 유일성을 증명하자. vi≠wi∈Wiv_i \neq w_i \in \mathbf{W} _i 에 대하여 v=w1+w2+⋯+wkv = w_1 + w_2 + \dots + w_k 가 성립한다고 하면 다음이 성립한다.

    (v1−w1)+(v2−w2)+⋯+(vk−wk)=v−v=0 (v_1 - w_1) + (v_2 - w_2) + \dots + (v_k - w_k) = v - v = 0

    vi−wi∈Wiv_i - w_i \in \mathbf{W} _i 인데 2) 를 가정했으므로 vi−wi=0⟹vi=wiv_i - w_i = 0 \implies v_i = w_i 이다. 이는 모순이다. ■

  • 3 에서 4 를 도출하는 증명

    3) 을 가정했으므로 V=∑i=1kWi\mathbf{V} = \displaystyle \sum_{i=1}^{k}\mathbf{W} _i 이다. 집합 γi\gamma _i 는 모든 vi∈Wiv_i \in \mathbf{W} _i 를 생성한다. 따라서 집합 ⋃γi\displaystyle \bigcup_{}^{}\gamma _i 로 모든 ∑i=1kvi∈V\displaystyle \sum_{i=1}^{k}v_i \in \mathbf{V} 를 생성할 수 있다.

    이 생성집합이 일차독립임을 보이면 기저이므로 증명이 끝난다. j∈{1,2,…,∣γi∣}j \in \{1,2, \dots, |\gamma _i|\} 에 대한 ∑i=1k∑j=1∣γi∣aijvij=0\displaystyle \sum_{i=1}^{k}\displaystyle \sum_{j=1}^{|\gamma _i|}a _{ij} v _{ij} = 0 인 벡터 vij∈γiv _{ij} \in \gamma _i 와 스칼라 aija _{ij} 가 존재한다. wi=∑j=1∣γi∣aijvijw_i = \displaystyle \sum_{j=1}^{|\gamma _i|}a _{ij}v _{ij} 로 두면 wi∈span⁡(γi)=Wiw_i \in \operatorname{span} (\gamma _i) = \mathbf{W} _i 이고 다음이 성립한다.

    w1+w2+⋯+wk=∑i=1k∑j=1∣γi∣aijvij=0 w_1 + w_2 + \dots + w_k = \sum_{i=1}^{k}\sum_{j=1}^{|\gamma _i|}a _{ij}v _{ij} = 0

    부분공간은 벡터공간이므로 0∈Wi0 \in \mathbf{W} _i 이다. 따라서 w1=0,w2=0,…,wk=0w_1 = 0, w_2 = 0, \dots, w_k = 0 을 가정할 경우 w1+w2+⋯+wk=0+0+⋯+0=0w_1 + w_2 + \dots + w_k = 0+0+\dots+0 = 0 이다. 3) 을 가정했는데 3) 에 따르면 이 표현은 유일하다. 즉, wi≠0w_i \neq 0 일 경우 w1+w2+⋯+wk=0w_1 + w_2 + \dots + w_k = 0 는 성립하지 않는다. 그러므로 wi=0w_i = 0 이다. 이는 다음이 성립함을 뜻한다.

    0=wi=∑j=1∣γi∣aijvij 0 = w_i = \sum_{j=1}^{|\gamma _i|} a _{ij}v _{ij}

    γi\gamma _i 는 일차독립이므로 위 식이 성립하기 위한 스칼라는 영벡터의 자명한 표현 뿐이다. 즉, aij=0a _{ij} = 0 이다. 이는 ⋃γi\displaystyle \bigcup_{}^{}\gamma _i 가 일차독립임을 뜻한다. ■

  • 4 에서 5 를 도출하는 증명

    4) 를 가정하면 5) 가 바로 나온다.

  • 5 에서 1 을 도출하는 증명

    문제 1.4-14 에 의하여 다음이 성립한다.

    V=span⁡(γ1∪γ2∪⋯∪γk)=span⁡(γ1)+span⁡(γ2)+⋯+span⁡(γk)=∑i=1kWi \begin{align}\begin{split} \mathbf{V} &= \operatorname{span} (\gamma _1 \cup \gamma _2 \cup \dots \cup \gamma _k) \\ &= \operatorname{span} (\gamma _1) + \operatorname{span} (\gamma _2) + \dots + \operatorname{span} (\gamma _k) = \sum_{i=1}^{k}\mathbf{W} _i\\ \end{split}\end{align} \tag*{}

    어떤 jj 와 영이 아닌 벡터 v∈Vv \in \mathbf{V} 에 대하여 v∈Wj∩∑i≠jWiv \in \mathbf{W} _j \cap \displaystyle \sum_{i \neq j}^{}\mathbf{W} _i 를 가정하면 v∈Wj=span⁡(γj)∧v∈∑i≠jWi=span⁡(⋃i≠jγi)v \in \mathbf{W} _j = \operatorname{span} (\gamma _j) \land v \in \displaystyle \sum_{i \neq j}^{}\mathbf{W} _i = \operatorname{span} \bigg (\bigcup_{i \neq j}^{}\gamma i\bigg ) 이다. 따라서 vv 는 γj\gamma _j 와 ⋃i≠jγi\displaystyle \bigcup_{i \neq j}^{}\gamma _i 의 자명하지 않은 일차결합이다. 그러므로 vv 를 ⋃i=1kγi\displaystyle \bigcup_{i=1}^{k}\gamma _i 의 일차결합으로 표현하는 방식이 유일하지 않다. 이는 정리 1.8 에 의하여 모순이다. 따라서 Wj∩∑i≠jWi={0}\mathbf{W} _j \cap \displaystyle \sum_{i \neq j}^{}\mathbf{W} _i = \{0\} 이다. ■

정리 5.10

유한차원 벡터공간 V\mathbf{V} 의 선형연산자 T⁡\operatorname{T} 가 대각화가능인 것과 V\mathbf{V} 가 T⁡\operatorname{T} 의 고유공간의 직합인 것은 동치이다.

  • 증명

    T⁡\operatorname{T} 의 서로 다른 고윳값을 λ1,λ2,…,λk\lambda _1, \lambda _2, \dots , \lambda _k 라 하자.

    T⁡\operatorname{T} 가 대각화가능임을 가정하자. 각 ii 에 대한 고유공간 Eλi\mathbf{E}_{\lambda_i} 의 순서기저를 γi\gamma _i 라 하자. 정리 5.8 은 ⋃γi\bigcup_{}^{}\gamma _i 가 V\mathbf{V} 의 기저임을 말해준다. 이로써 정리 5.9 의 4) 가 충족된다. 정리 5.9 의 1) 은 4) 와 진리값이 같으므로 V=⨁Eλi\mathbf{V} = \bigoplus_{}^{}\mathbf{E}_{\lambda_i} 이다. ▲

    V\mathbf{V} 가 T⁡\operatorname{T} 의 고유공간의 직합임을 가정하자. 각 ii 에 대하여 Eλi\mathbf{E}_{\lambda_i} 의 순서기저 γi\gamma _i 가 존재한다. 정리 5.9 의 1) 이 참이므로 4) 도 참이 되어 ⋃γi\bigcup_{}^{}\gamma _i 는 V\mathbf{V} 의 기저가 된다. 이 기저는 T⁡\operatorname{T} 의 고유벡터로 이루어진 기저이므로 T⁡\operatorname{T} 는 대각화가능하다. ■

  • 예시

    벡터공간 R5\R ^{5} 에 부분공간 W={(x1,x2,x3,x4,x5):x5=0},W1={(a,b,0,0,0):a,b∈R},W2={(0,0,c,0,0):c∈R},W3={(0,0,0,d,0):d∈R}\mathbf{W} = \{(x_1, x_2, x_3, x_4, x_5) : x_5 = 0\}, \mathbf{W}_1 = \{(a, b, 0, 0, 0) : a, b \in \R\}, \mathbf{W}_2 = \{(0, 0, c, 0, 0) : c \in \R\}, \mathbf{W}_3 = \{(0, 0, 0, d, 0) : d \in \R\} 이 존재한다. (a,b,c,d,0)∈W(a, b, c, d, 0) \in \mathbf{W} 에 대하여 다음이 성립한다.

    (a,b,c,d,0)=(a,b,0,0,0)+(0,0,c,0,0)+(0,0,0,d,0)∈W1+W2+W3 (a, b, c, d, 0) = (a, b, 0, 0, 0) + (0, 0, c, 0, 0) + (0, 0, 0, d, 0) \in \mathbf{W} _1 +\mathbf{W} _2 +\mathbf{W} _3
    W1∩(W2+W3)=W2∩(W1+W3)=W3∩(W1+W2)={0} \mathbf{W} _1 \cap (\mathbf{W} _2 + \mathbf{W} _3) = \mathbf{W} _2 \cap (\mathbf{W} _1 + \mathbf{W} _3) = \mathbf{W} _3 \cap (\mathbf{W} _1 + \mathbf{W} _2) =\{0\}

    그러므로 W=⨁i=13Wi\mathbf{W} = \displaystyle \bigoplus_{i=1}^{3}\mathbf{W} _i 이다.

    벡터공간 R4\R ^{4} 의 선형연산자 T⁡(a,b,c,d)=(a,b,2c,3d)\operatorname{T} (a, b, c, d) = (a, b, 2c, 3d) 에 대하여 T⁡\operatorname{T} 가 대각화가능이고 고윳값 1,2,31, 2, 3 을 갖는다는 것을 알 수 있다. 이때 각 고윳값에 대응하는 고유공간들이 각각 W1,W2,W3\mathbf{W} _1, \mathbf{W} _2, \mathbf{W} _3 와 같음을 알 수 있다. 이때 정리를 사용하면 R4=W1⊕W2⊕W3\R ^{4} = \mathbf{W} _1 \oplus \mathbf{W} _2 \oplus \mathbf{W} _3 임을 알 수 있다.

Invariant Subspace✔

불변 부분공간(invariant subspace)

벡터공간 V\mathbf{V} 와 부분공간 W\mathbf{W} 와 선형연산자 T⁡\operatorname{T} 에 대하여 T⁡(W)⊆W\operatorname{T} (\mathbf{W} ) \subseteq \mathbf{W} 인 W\mathbf{W} 를 V\mathbf{V} 의 T⁡\operatorname{T}-불변 부분공간이라 한다.

  • 즉, ∀v∈W:T⁡(v)∈W\forall v \in \mathbf{W} : \operatorname{T} (v) \in \mathbf{W} 이면 W\mathbf{W} 가 V\mathbf{V} 의 T⁡\operatorname{T}-불변 부분공간이라는 것이다.

    쉽게 말해, 부분공간의 원소가 T⁡\operatorname{T} 를 통과해서 나왔는데도 부분공간에 속했으면 T⁡\operatorname{T}-불변이다.

문제 5.4-3

벡터공간 V\mathbf{V} 와 선형연산자 T⁡\operatorname{T} 에 대하여 다음 부분공간은 T⁡\operatorname{T}-불변이다.

  1. {0}\{0\}

  2. V\mathbf{V}

  3. im⁡(T⁡)\operatorname{im}(\operatorname{T})

  4. ker⁡(T⁡)\ker(\operatorname{T})

  5. T⁡\operatorname{T} 의 고윳값 λ\lambda 에 대한 Eλ\mathbf{E}_{\lambda}

  • 증명

    벡터공간 V\mathbf{V} 의 선형연산자 T⁡\operatorname{T} 에 대하여 다음의 부분공간들이 T⁡\operatorname{T}-불변임을 확인해보자.

    {0}\{0\}:

    선형변환의 성질 에 의하여 T⁡(0)=0∈{0}\operatorname{T} (0) = 0 \in \{0\} 이므로 {0}\{0\} 는 T⁡\operatorname{T}-불변이다.

    V\mathbf{V}:

    선형연산자 T⁡:V→V\operatorname{T} : \mathbf{V} \to \mathbf{V} 의 공역이 V\mathbf{V} 이므로 T⁡(V)⊂V\operatorname{T} (\mathbf{V} ) \subset \mathbf{V} 이다. 따라서 V\mathbf{V} 는 T⁡\operatorname{T}-불변이다.

    im⁡(T⁡)\operatorname{im} (\operatorname{T}):

    im⁡(T⁡)⊂V\operatorname{im} (\operatorname{T}) \subset \mathbf{V} 인 V\mathbf{V} 에 대하여 T⁡(V)=im⁡(T⁡)\operatorname{T} (\mathbf{V} ) = \operatorname{im} (\operatorname{T}) 이다. 따라서 T⁡(im⁡(T⁡))⊂T⁡(V)=im⁡(T⁡)\operatorname{T} (\operatorname{im} (\operatorname{T}) ) \subset \operatorname{T} (\mathbf{V} ) = \operatorname{im} (\operatorname{T}) 이다.

    ker⁡(T⁡)\ker (\operatorname{T}):

    T⁡(ker⁡(T⁡))={0}\operatorname{T} (\ker (\operatorname{T}) ) = \{0\} 이므로 T⁡(ker⁡(T⁡))={0}⊂ker⁡(T⁡)\operatorname{T} (\ker (\operatorname{T}) ) = \{0\} \subset \ker (\operatorname{T}) 이다.

    T⁡\operatorname{T} 의 고윳값 λ\lambda 에 대한 Eλ\mathbf{E}_{\lambda}:

    x∈Eλx \in \mathbf{E}_{\lambda} 에 대하여 T⁡(x)=λx\operatorname{T} (x) = \lambda x 이다. T⁡(λx)=λT⁡(x)=λ⋅λx\operatorname{T} (\lambda x) = \lambda \operatorname{T} (x) = \lambda \cdot \lambda x 이다. 벡터공간은 스칼라곱에 닫혀있으므로 λx∈V\lambda x \in \mathbf{V} 이다. 따라서 λx∈V⟹λx∈Eλ\lambda x \in \mathbf{V} \implies \lambda x \in \mathbf{E}_{\lambda} 이다. 따라서 T⁡(Eλ)⊂Eλ\operatorname{T} (\mathbf{E}_{\lambda} ) \subset \mathbf{E}_{\lambda} 이다.

문제 5.4-4

벡터공간 V\mathbf{V} 의 선형연산자 T⁡\operatorname{T} 와 T⁡\operatorname{T}-불변 부분공간 W\mathbf{W} 와 임의의 다항식 g(t)g(t) 에 대하여 W\mathbf{W} 는 g(T⁡)g(\operatorname{T})-불변이다.

  • 증명

    g(T⁡)g(\operatorname{T}) 를 스칼라 a0,a1,…,ana_0, a_1, \dots, a_n 에 대하여 다음과 같이 두자.

    g(T⁡)=anT⁡n+⋯+a1T⁡+a0I⁡ g(\operatorname{T}) = a_n \operatorname{T}^{n} + \dots + a_1 \operatorname{T} + a_0 \operatorname{I}

    ∀k∈N,∀w∈W:T⁡k(w)∈W\forall k \in \N, \forall w \in \mathbf{W} : \operatorname{T}^{k}(w) \in \mathbf{W} 이다. W\mathbf{W} 는 부분공간이므로 합과 스칼라곱에 대하여 닫혀있다. 따라서 w∈Ww \in \mathbf{W} 에 대하여 g(T⁡)(w)g(\operatorname{T})(w) 의 모든 항은 W\mathbf{W} 에 속하고 결국 g(T⁡)(w)∈Wg(\operatorname{T})(w) \in \mathbf{W} 이다. ■

Cyclic subspace✔

순환 부분공간(cyclic subspace)

벡터공간 V\mathbf{V} 의 선형연산자 T⁡\operatorname{T} 와 영이 아닌 벡터 x∈Vx \in \mathbf{V} 에 대하여 다음과 같은 부분공간 W\mathbf{W} 를 xx 에 의해 생성된 V\mathbf{V} 의 T⁡\operatorname{T}-순환 부분공간이라 한다.

W=span⁡{x,T⁡(x),T⁡2(x),…} \mathbf{W} = \operatorname{span} \{x, \operatorname{T} (x), \operatorname{T} ^{2}(x), \dots \}

  • 문제 5.4-31 은 순환 부분공간으로 행렬식 없이 선형연산자의 특성다항식을 구하는 방법을 말해준다.

  • 순환 부분공간은 대각화 불가능한 선형연산자의 행렬표현을 다룰 때 매우 중요한 역할을 한다.

  • 예시

    R3\R ^{3} 의 선형연산자 T⁡\operatorname{T} 를 T⁡(a,b,c)=(−b+c,a+c,3c)\operatorname{T}(a,b,c)=(-b+c,a+c,3c) 라고 정의하고 e1=(1,0,0)e_1 = (1, 0, 0) 에 의해 생성된 T⁡\operatorname{T}-순환 부분공간을 구해보자. 다음이 성립한다.

    T⁡(e1)=T⁡(1,0,0)=(0,1,0)=e2\operatorname{T}(e_1) = \operatorname{T}(1,0,0) = (0, 1,0) = e_2
    T⁡2(e1)=T⁡(T⁡(e1))=T⁡(e2)=(−1,0,0)=−e1\operatorname{T}^{2}(e_1) = \operatorname{T}(\operatorname{T}(e_1)) = \operatorname{T}(e_2) = (-1,0,0) = -e_1

    그러므로 e1e_1 에 의해 생성된 T⁡\operatorname{T}-순환 부분공간은 다음과 같다.

    span⁡{e1,T⁡(e1),T⁡2(e1),…}=span⁡{e1,e2}={(s,t,0):s,t∈R} \operatorname{span} \{e_1, \operatorname{T}(e_1), \operatorname{T}^{2}(e_1), \dots\} = \operatorname{span} \{e_1, e_2\} = \{(s, t, 0) : s, t \in \R\}

문제 5.4-11

벡터공간 V\mathbf{V} 의 선형연산자 T⁡\operatorname{T} 와 영이 아닌 벡터 v∈Vv \in \mathbf{V}, vv 에 의해 생성된 V\mathbf{V} 의 T⁡\operatorname{T}-순환 부분공간 W\mathbf{W} 에 대하여 다음이 성립한다.

  1. W\mathbf{W} 는 T⁡\operatorname{T}-불변이다.

  2. vv 를 포함하는 V\mathbf{V} 의 임의의 T⁡\operatorname{T}-불변 부분공간은 W\mathbf{W} 를 포함한다.

  • 이 정리는 T⁡\operatorname{T}-순환 부분공간이 T⁡\operatorname{T}-불변임을 말해준다.

  • 이 정리는 xx 를 포함하는 T⁡\operatorname{T}-불변 부분공간이 반드시 xx 에 의해 생성된 T⁡\operatorname{T}-순환 부분공간을 포함함을 말해준다. 즉, T⁡\operatorname{T}-순환 부분공간은 xx 를 포함하는 가장 작은 T⁡\operatorname{T}-불변 부분공간이다.

    가령 벡터공간 V\mathbf{V} 의 xx 를 포함하는 T⁡\operatorname{T}-불변 부분공간 W1,W2,…,Wn\mathbf{W}_1, \mathbf{W}_2, \dots, \mathbf{W}_n 과 xx 에 의해 생성된 T⁡\operatorname{T}-순환 부분공간 Z\mathbf{Z} 를 가정하면 다음이 성립한다.

    Z⊂W1,Z⊂W2,…,Z⊂Wn \mathbf{Z} \subset \mathbf{W}_1, \mathbf{Z} \subset \mathbf{W}_2, \dots, \mathbf{Z} \subset \mathbf{W}_n

    이는 정리 1.11 와 그 따름정리에 의해 Z\mathbf{Z} 의 기저가 다른 모든 T⁡\operatorname{T}-불변 부분공간의 기저에 포함됨을 뜻한다. 따라서 T⁡\operatorname{T}-순환 부분공간은 가장 작은 T⁡\operatorname{T}-불변 부분공간이 된다.

  • 증명

    집합 β={v,T⁡(v),T⁡2(v),…}\beta = \{v, \operatorname{T}(v), \operatorname{T}^{2}(v), \dots\} 가 W\mathbf{W} 를 생성한다. 다음을 만족하는 무한한 스칼라 a0,a1,a2,…a_0, a_1, a_2, \dots 가 존재한다.

    x∈W⟹x=a0v+a1T⁡(v)+a2T⁡2(v)+… x \in \mathbf{W} \implies x = a_0v + a_1 \operatorname{T}(v) + a_2 \operatorname{T}^{2}(v) + \dots
    ⟹T⁡(x)=a0T⁡(v)+a1T⁡2(v)+a2T⁡3(v)+… \implies \operatorname{T}(x) = a_0 \operatorname{T}(v) + a_1 \operatorname{T}^{2}(v) + a_2 \operatorname{T}^{3}(v) + \dots

    T⁡(x)\operatorname{T}(x) 는 β\beta 에 의한 일차결합이므로 T⁡(x)∈W\operatorname{T}(x) \in \mathbf{W} 이다. 따라서 W\mathbf{W} 는 T⁡\operatorname{T}-불변이다. ▲

    T⁡\operatorname{T}-불변 부분공간 Z\mathbf{Z} 가 v∈Zv \in \mathbf{Z} 를 만족하면 다음이 성립한다.

    v∈Z⟹T⁡(v)∈Z⟹T⁡2(v)∈Z⟹… v \in \mathbf{Z} \implies \operatorname{T}(v) \in \mathbf{Z} \implies \operatorname{T}^{2}(v) \in \mathbf{Z} \implies \dots

    그러므로 β⊂Z\beta \subset \mathbf{Z} 이다. Z\mathbf{Z} 가 W\mathbf{W} 의 기저를 포함하므로 W\mathbf{W} 의 모든 벡터는 Z\mathbf{Z} 에 포함된다. 즉, W⊂Z\mathbf{W} \subset \mathbf{Z} 이다. ■

restriction✔

제한(restriction)

벡터공간 V\mathbf{V} 의 선형연산자 T⁡:V→V\operatorname{T}:\mathbf{V} \to \mathbf{V} 와 T⁡\operatorname{T}-불변 부분공간 W\mathbf{W} 에 대하여 T⁡\operatorname{T} 를 W\mathbf{W} 로 제한한 T⁡W\operatorname{T}_{\mathbf{W}} 는 T⁡\operatorname{T} 의 정의역과 공역을 W\mathbf{W} 로 제한한 함수 T⁡W:W→W\operatorname{T}_{\mathbf{W}}:\mathbf{W}\to \mathbf{W} 이다.

  • 함수의 제한은 정의역만 축소시키는 것으로 정의되지만, 이 경우 정의역이 T⁡\operatorname{T}-불변 부분공간으로 축소되므로 공역도 어차피 T⁡\operatorname{T}-불변 부분공간으로 축소된다.

  • T⁡W\operatorname{T}_{\mathbf{W}} 는 선형변환이다.(문제 5.4-7) 즉, T⁡W\operatorname{T}_{\mathbf{W}} 는 W\mathbf{W} 의 선형연산자이다.

  • T⁡W\operatorname{T}_{\mathbf{W}} 는 T⁡\operatorname{T} 의 성질을 그대로 상속한다.

문제 5.4-12

유한차원 벡터공간 V\mathbf{V} 의 선형연산자 T⁡\operatorname{T} 와 T⁡\operatorname{T}-불변 부분공간 W\mathbf{W} 에 대한 T⁡W\operatorname{T}_{\mathbf{W}} 의 순서기저 γ={v1,v2,…,vk}\gamma = \{v_1, v_2, \dots, v_k\} 를 확장하여 V\mathbf{V} 의 순서기저 β={v1,v2,…,vk,vk+1,…,vn}\beta = \{v_1, v_2, \dots, v_k, v _{k+1}, \dots, v_n\} 을 만들고 A=[T⁡]β,B1=[T⁡W]γA = [\operatorname{T}]_{\beta }, B_1 = [\operatorname{T}_{\mathbf{W}}]_{\gamma } 로 두자.

영행렬 OO 에 대하여 다음이 성립한다.

A=(B1B2OB3) A = \begin{pmatrix} B_1&B_2\\ O&B_3\\ \end{pmatrix}

  • 증명

    i∈{1,…,k}i \in \{1, \dots, k\} 에 대하여 AA 의 ii 열은 다음과 같다.

    T⁡(vi)=∑i=1naijvi∈W \operatorname{T}(v_i) = \sum_{i=1}^{n}a _{ij}v_i \in \mathbf{W}

    vi∈Wv_i \in \mathbf{W} 이므로 T⁡(vi)∈W\operatorname{T}(v_i) \in \mathbf{W} 이다. 만약 ∑i=k+1naijvi≠0\sum_{i=k+1}^{n}a _{ij}v_i \neq 0 이면 T⁡(vi)\operatorname{T}(v_i) 를 W\mathbf{W} 의 기저로 표현하는 것이 불가능하므로 T⁡(vi)∉W\operatorname{T}(v_i) \not\in \mathbf{W} 이다. 이는 모순이다. 따라서 ∑i=k+1nvi=0\sum_{i=k+1}^{n}v_i = 0 이다. 그러므로 AA 의 ii 열은 다음과 같다.

    T⁡(vi)=∑i=1kaijvi \operatorname{T}(v_i) = \sum_{i=1}^{k}a _{ij}v_i

    이로써 모든 증명이 끝났다. ■

정리 5.20

유한차원 벡터공간 V\mathbf{V} 의 선형연산자 T⁡\operatorname{T} 와 T⁡\operatorname{T}-불변 부분공간 W\mathbf{W} 에 대한 T⁡W\operatorname{T}_{\mathbf{W}} 의 특성다항식은 T⁡\operatorname{T} 의 특성다항식을 나눈다.

  • 이 정리는 선형연산자와 T⁡\operatorname{T}-불변 부분공간에 의한 제한과의 관계를 말해준다.

  • 증명

    W\mathbf{W} 의 순서기저를 γ={v1,v2,…,vk}\gamma = \{v_1, v_2, \dots, v_k\} 라 하면 γ\gamma 를 확장하여 V\mathbf{V} 의 순서기저 β={v1,v2,…,vk,vk+1,…,vn}\beta = \{v_1, v_2, \dots, v_k, v _{k+1}, \dots, v_n\} 을 만들 수 있다. A=[T⁡]β,B1={T⁡W}γA = [\operatorname{T}]_{\beta }, B_1 = \{\operatorname{T}_{\mathbf{W}}\}_{\gamma } 라 하면 문제 5.4-12 에 의하여 다음이 성립한다.

    A=(B1B2OB3) A = \begin{pmatrix} B_1&B_2\\ O&B_3\\ \end{pmatrix}

    T⁡\operatorname{T} 의 특성다항식 f(t)f(t), T⁡W\operatorname{T}_{\mathbf{W}} 의 특성다항식 g(t)g(t) 에 대하여 문제 4.3-21 에 의하여 다음이 성립한다.

    f(t)=det⁡(A−tIn)=det⁡(B1−tIkB2OB3−tIn−k)=g(t)det⁡(B3−tIn−k) f(t) = \det(A - tI_n) = \det \begin{pmatrix} B_1-tI_k&B_2\\ O&B_3-tI _{n-k}\\ \end{pmatrix} = g(t) \det(B_3-tI _{n-k})

    따라서 g(t)g(t) 는 f(t)f(t) 를 나눈다. ■

문제 5.4-19

스칼라 a0,a1,…,ak−1∈Fa_0, a_1, \dots, a _{k-1} \in \mathbf{F} 와 다음과 같이 정의된 행렬 A∈Fk×kA \in \mathbf{F} ^{k \times k} 의 특성다항식은 (−1)k(a0+a1t+⋯+ak−1tk−1+tk)(-1) ^{k}(a_0+ a_1t+ \dots + a _{k-1}t^{k-1} + t ^{k}) 이다.

A=(00…0−a010…0−a101…0−a2⋮⋮⋱⋮⋮00…1−ak−1) A= \begin{pmatrix} 0&0&\dots&0&-a_0\\ 1&0&\dots&0&-a_1\\ 0&1&\dots&0&-a_2\\ \vdots& \vdots& \ddots& \vdots& \vdots \\ 0&0&\dots&1&-a _{k-1}\\ \end{pmatrix}

  • 증명

    k=2k = 2 을 가정하면 A=(0−a01−a1)A = \begin{pmatrix} 0&-a_0\\ 1&-a_1\\ \end{pmatrix} 이다. 다음이 성립한다.

    f(t)=det⁡(A−tI2)=det⁡(−t−a01−a1−t)=t(a1+t)+a0=(−1)2(a0+a1t+t2)▲f(t) = \det(A - tI_2) = \det \begin{pmatrix} -t&-a_0\\ 1&-a_1-t\\ \end{pmatrix} = t(a_1+t) + a_0 = (-1) ^{2}(a_0 + a_1t + t ^{2}) \tag*{▲}

    k−1k-1 에서 정리가 성립함을 가정하고 kk 에서 정리가 성립함을 증명하자. B=A−tIkB = A - tI_k 로 두면 A∈Fk×kA \in \mathbf{F} ^{k \times k} 의 특성다항식은 다음과 같다.

    det⁡(B)=det⁡(−t0…0−a01−t…0−a101…0−a2⋮⋮⋱⋮⋮00…1−ak−1−t)=(−1)1+1B11det⁡(B~11)+(−1)1+kB1kdet⁡(B~1k)=−tdet⁡(B~11)+(−1)1+k⋅(−a0)⋅1 \begin{align}\begin{split} \det(B) &= \det \begin{pmatrix} -t&0&\dots&0&-a_0\\ 1&-t&\dots&0&-a_1\\ 0&1&\dots&0&-a_2\\ \vdots& \vdots& \ddots& \vdots& \vdots \\ 0&0&\dots&1&-a _{k-1}-t\\ \end{pmatrix} \\ &= (-1)^{1 + 1}B _{11} \det(\tilde{B}_{11}) + (-1) ^{1 + k}B _{1k}\det(\tilde{B}_{1k}) \\ &= -t \det(\tilde{B}_{11}) + (-1) ^{1 + k}\cdot (-a_0) \cdot 1 \\ \end{split}\end{align} \tag*{}

    B~11\tilde{B}_{11} 은 A~11\tilde{A}_{11} 의 특성다항식이다. k−1k-1 에서 정리가 성립하므로 det⁡(B~11)\det(\tilde{B}_{11}) 은 적절한 스칼라 b0,b1,…,bk−1∈Fb_0, b_1, \dots, b_{k-1} \in \mathbf{F} 에 대하여 (−1)k−1(b0+b1t+⋯+bk−2tk−2+tk−1)(-1) ^{k-1}(b_0+ b_1t+ \dots + b_{k-2}t^{k-2} + t ^{k-1}) 이다. 따라서 다음이 성립한다.

    det⁡(A−tIk)=−t⋅(−1)k−1(b0+b1t+⋯+bk−2tk−2+tk−1)+(−1)k⋅a0=(−1)k(b0t+b1t2+⋯+bk−2tk−1+tk)+(−1)k⋅a0=(−1)k(a0+b0t+b1t2+⋯+bk−2tk−1+tk)=(−1)k(a0+a1t+a2t2+⋯+ak−1tk−1+tk) \begin{align}\begin{split} \det(A - tI_k) &= -t \cdot (-1) ^{k-1}(b_0+ b_1t+ \dots + b_{k-2}t^{k-2} + t ^{k-1}) + (-1) ^{k}\cdot a_0 \\ &= (-1) ^{k}(b_0t+ b_1t ^{2}+ \dots + b_{k-2}t^{k-1} + t ^{k}) + (-1) ^{k}\cdot a_0 \\ &= (-1) ^{k}(a_0 + b_0t+ b_1t ^{2}+ \dots + b_{k-2}t^{k-1} + t ^{k}) \\ &= (-1) ^{k}(a_0 + a_1t+ a_2t ^{2}+ \dots + a_{k-1}t^{k-1} + t ^{k}) \\ \end{split}\end{align} \tag*{}

    단순히 bi=ai+1b_i = a _{i+1} 로 선택하면 위와 같은 결론을 얻을 수 있다. 정리가 임의의 스칼라들에 대하여 성립하므로 이렇게 선택해도 괜찮다. ■

정리 5.21

유한차원 벡터공간 V\mathbf{V} 의 선형연산자 T⁡\operatorname{T} 와 영이 아닌 벡터 v∈Vv \in \mathbf{V} 에 의해 생성된 T⁡\operatorname{T}-순환 부분공간 W\mathbf{W} 에 대하여 k=dim⁡(W)k = \dim (\mathbf{W}) 이면 다음이 성립한다.

  1. {v,T⁡(v),…,T⁡k−1(v)}\{v, \operatorname{T}(v), \dots, \operatorname{T}^{k-1}(v)\} 는 W\mathbf{W} 의 기저이다.

  2. 스칼라 a0,a1,…,ak−1a_0, a_1, \dots, a _{k-1} 에 대하여 a0v+a1T⁡(v)+⋯+ak−1T⁡k−1(v)+T⁡k(v)=0a_0v + a_1 \operatorname{T}(v) + \dots + a _{k-1}\operatorname{T}^{k-1}(v)+\operatorname{T}^{k}(v) = 0 이면 T⁡W\operatorname{T}_{\mathbf{W}} 의 특성다항식은 f(t)=(−1)k(a0+a1t+⋯+ak−1tk−1+tk)f(t) = (-1)^{k}(a_0+a_1t+\dots+a _{k-1}t ^{k-1}+t ^{k}) 이다.

  • 정리 5.20 은 T⁡W\operatorname{T}_{\mathbf{W}} 의 특성다항식으로 T⁡\operatorname{T} 의 특성다항식의 정보를 얻게 해준다. 이 정리는 T⁡W\operatorname{T}_{\mathbf{W}} 의 특성다항식을 쉽게 얻게 해준다는 관점에서 순환 부분공간의 유용함을 증명해준다.

  • 1) 는 T⁡\operatorname{T}-순환 부분공간을 정의하기 위하여 사용된 생성집합

    span⁡({v,T⁡(v),T⁡2(v),…}) \operatorname{span} (\{v, \operatorname{T} (v), \operatorname{T} ^{2}(v), \dots \})

    에서 T⁡k(v)\operatorname{T}^{k}(v) 이상의 것들은 불필요함을 알려준다. 또한 T⁡\operatorname{T}-순환 부분공간의 기저를 쉽게 알 수 있는 방법을 알려준다.

  • 2) 는 T⁡W\operatorname{T}_{\mathbf{W}} 의 특성다항식을 쉽게 구하는 방법을 알려준다. 즉 T⁡k(v)\operatorname{T}^{k}(v) 를 기저로 표현하는 일차결합의 계수만 알아내면 특성다항식을 바로 구할 수 있다는 것이다. 너무 자명하지만, 이 일차결합 표현은 반드시 존재한다.

  • 증명

    v≠0v \neq 0 이므로 {v}\{v\} 는 일차독립이다. β={v,T⁡(v),…,T⁡j−1(v)}\beta = \{v, \operatorname{T}(v), \dots, \operatorname{T}^{j-1}(v)\} 가 일차독립이 되게 하는 가장 큰 자연수 jj 가 존재한다. V\mathbf{V} 가 유한차원이므로 유한한 기저보다 기수가 작은 일차독립 집합들이 존재하기 때문이다.

    Z=span⁡(β)\mathbf{Z}=\operatorname{span} (\beta ) 로 두면 β\beta 는 Z\mathbf{Z} 의 기저이다. jj 가 β\beta 를 일차독립이 되게 하기 위한 마지막 자연수이므로 j+1j+1 에 대하여 일차종속이 되므로 β\beta 의 일차결합으로 T⁡j(v)\operatorname{T}^{j}(v) 를 표현할 수 있다. 따라서 정리 1.7 의 세번째 명제에 의하여 T⁡j(v)∈Z\operatorname{T}^{j}(v) \in \mathbf{Z} 이다.

    w∈Zw \in \mathbf{Z} 이면 w=b0v+b1T⁡(v)+⋯+bj−1T⁡j−1(v)w = b_0v + b_1 \operatorname{T}(v) + \dots + b_{j-1}\operatorname{T}^{j-1}(v) 인 스칼라 b0,b1,…,bj−1b_0, b_1, \dots, b _{j-1} 가 존재한다. 이 식에 T⁡\operatorname{T} 를 씌우면 다음과 같다.

    T⁡(w)=b0T⁡(v)+b1T⁡2(v)+⋯+bj−1T⁡j(v) \operatorname{T}(w) = b_0 \operatorname{T}(v) + b_1 \operatorname{T}^{2}(v) + \dots + b _{j-1} \operatorname{T}^{j}(v)

    T⁡(w)\operatorname{T}(w) 는 Z\mathbf{Z} 의 기저의 일차결합이므로 T⁡(w)∈Z\operatorname{T}(w) \in \mathbf{Z} 이다. 따라서 Z\mathbf{Z} 는 T⁡\operatorname{T}-불변이다. 문제 5.4-11 에 의하여 W\mathbf{W} 는 vv 를 포함하는 가장 작은 T⁡\operatorname{T}-불변 부분공간이므로 W⊂Z\mathbf{W}\subset \mathbf{Z} 이다.

    그런데 Z\mathbf{Z} 의 생성집합 β\beta 가 W\mathbf{W} 의 생성집합에 포함되므로 자명하게 Z⊂W\mathbf{Z}\subset \mathbf{W} 이다. 따라서 Z=W\mathbf{Z} = \mathbf{W} 이다. 그러므로 β\beta 는 W\mathbf{W} 의 기저이고 dim⁡(W)=j=k\dim (\mathbf{W})=j=k 이다. ▲

    이제 β={v,T⁡W(v),…,T⁡Wk−1(v)}\beta = \{v, \operatorname{T}_{\mathbf{W}}(v), \dots, \operatorname{T}_{\mathbf{W}}^{k-1}(v)\} 가 W\mathbf{W} 의 순서기저임을 가정할 수 있다. [T⁡W]β[\operatorname{T}_{\mathbf{W}}]_{\beta } 는 다음과 같다.

    T⁡W(v)=1⋅T⁡W(v) \operatorname{T}_{\mathbf{W}}(v) = 1 \cdot \operatorname{T}_{\mathbf{W}}(v)
    T⁡W(T⁡W(v))=1⋅T⁡W2(v) \operatorname{T}_{\mathbf{W}}(\operatorname{T}_{\mathbf{W}}(v)) = 1 \cdot \operatorname{T}_{\mathbf{W}}^{2}(v)
    T⁡W(T⁡Wk−2(v))=1⋅T⁡Wk−1(v) \operatorname{T}_{\mathbf{W}}(\operatorname{T}_{\mathbf{W}}^{k-2}(v)) = 1 \cdot \operatorname{T}_{\mathbf{W}}^{k-1}(v)
    T⁡W(T⁡Wk−1(v))=T⁡Wk(v)=−a0v−a1T⁡(v)−⋯−ak−1T⁡k−1(v) \operatorname{T}_{\mathbf{W}}(\operatorname{T}_{\mathbf{W}}^{k-1}(v)) = \operatorname{T}_{\mathbf{W}}^{k}(v) = -a_0v - a_1 \operatorname{T}(v) - \dots - a _{k-1}\operatorname{T}^{k-1}(v)
    ⟹[T⁡W]β=(00…0−a010…0−a1⋮⋮⋱⋮⋮00…1−ak−1) \implies [\operatorname{T}_{\mathbf{W}}]_{\beta } = \begin{pmatrix} 0&0&\dots&0&-a_0\\ 1&0&\dots&0&-a_1\\ \vdots& \vdots& \ddots& \vdots&\vdots \\ 0&0&\dots&1&-a _{k-1}\\ \end{pmatrix}

    문제 5.4-19 에 의하여 [T⁡W]β[\operatorname{T}_{\mathbf{W}}]_{\beta } 의 특성다항식은 f(t)=(−1)k(a0+a1t+⋯+ak−1tk−1+tk)f(t) = (-1)^{k}(a_0+a_1t+\dots+a _{k-1}t ^{k-1}+t ^{k}) 이다. 선형연산자의 특성다항식은 선형연산자의 행렬표현의 특성다항식으로 정의되므로 증명이 끝났다. ■

Cayley-Hamilton theorem✔

정리 5.22 케일리-해밀턴 정리(Cayley-Hamilton theorem)

유한차원 벡터공간 V\mathbf{V} 의 선형연산자 T⁡\operatorname{T} 와 T⁡\operatorname{T} 의 특성다항식 f(t)f(t) 에 대하여 f(T⁡)=T⁡0f(\operatorname{T}) = \operatorname{T}_0 이다.

  • 다항식에 선형연산자가 입력된 형태의 정의를 참고하자.

  • 이 정리는 정리 5.21 의 중요성을 보여준다. 왜냐하면 이 정리가 널리 사용되기 때문이다.

  • 증명

    ∀v∈V:f(T⁡)(v)=0\forall v \in \mathbf{V}: f(\operatorname{T})(v) = 0 을 보이면 된다. v=0v = 0 를 가정하면 f(T⁡)f(\operatorname{T}) 가 선형이므로 증명할 것이 없다. ▲

    v≠0v \neq 0 을 가정하자. vv 에 의해 생성된 T⁡\operatorname{T}-순환 부분공간 W\mathbf{W} 를 가정하고 dim⁡(W)=k\dim (\mathbf{W}) = k 로 두면 정리 5.21 의 첫번째 명제에 의하여 다음을 만족하는 스칼라 a0,a1,a2,…,ak−1a_0, a_1, a_2, \dots, a _{k-1} 가 존재한다.

    a0v+a1T⁡(v)+⋯+ak−1T⁡k−1(v)+T⁡k(v)=0 a_0v + a_1 \operatorname{T}(v) + \dots + a _{k-1}\operatorname{T}^{k-1}(v) + \operatorname{T}^{k}(v) = 0

    정리 5.21 의 두번째 명제에 의하여 T⁡W\operatorname{T}_{\mathbf{W}} 의 특성다항식은 다음과 같다.

    g(t)=(−1)k(a0+a1t+⋯+ak−1tk−1+tk) g(t) = (-1)^{k}(a_0 + a_1t+ \dots+ a _{k-1}t ^{k-1}+t ^{k})

    따라서 다음이 성립한다.

    g(T⁡)(t)=(−1)k(a0I⁡+a1T⁡+⋯+ak−1T⁡k−1+T⁡k)(v)=0 g(\operatorname{T})(t) = (-1)^{k}(a_0 \operatorname{I} + a_1 \operatorname{T}+ \dots+ a _{k-1} \operatorname{T} ^{k-1}+\operatorname{T}^{k})(v) = 0

    정리 5.20 은 g(t)g(t) 가 f(t)f(t) 나눈다는 것을 알려준다. 즉, 다음이 성립한다.

    f(T⁡)(v)=q(T⁡)g(T⁡)(v)=q(T⁡)(g(T⁡)(v))=q(T⁡)(0)=0 f(\operatorname{T})(v) = q(\operatorname{T})g(\operatorname{T})(v) = q(\operatorname{T})(g(\operatorname{T})(v)) = q(\operatorname{T})(0)=0

    따라서 f(T⁡)=T⁡0f(\operatorname{T}) = \operatorname{T}_0 이다. ■

  • 예시

    R2\R ^{2} 의 선형연산자 T⁡(a,b)=(a+2b,−2a+b)\operatorname{T}(a,b)=(a+2b, -2a+b) 와 T⁡\operatorname{T} 의 특성다항식 f(t)=det⁡([T⁡]β−tI)=det⁡(1−t2−21−t)=t2−2t+5f(t) = \det([\operatorname{T}]_{\beta }-tI) = \det \begin{pmatrix} 1-t&2\\ -2&1-t\\ \end{pmatrix}=t ^{2}-2t+5 에 대하여 f(T⁡)=T⁡2−2T⁡+5I⁡=T⁡0f(\operatorname{T}) = \operatorname{T}^{2}-2 \operatorname{T}+5 \operatorname{I} = \operatorname{T}_0 이다.

정리 5.22 따름정리

n×nn \times n 행렬 AA 와 그 특성다항식 f(t)f(t) 에 대하여 f(A)=Of(A) = O 이다.
  • 증명

Invariant subspace and Direct sum✔

정리 5.23

유한차원 벡터공간 V\mathbf{V} 의 선형연산자 T⁡\operatorname{T} 와 i∈{1,…,k}i \in \{1,\dots,k\} 에 대하여 Wi\mathbf{W}_i 가 T⁡\operatorname{T}-불변이고 V=⨁i=1kWi\mathbf{V} = \displaystyle \bigoplus_{i=1}^{k}\mathbf{W}_i 가 성립함을 가정하자.

T⁡Wi\operatorname{T}_{\mathbf{W}_i} 의 특성다항식 fi(t)f_i(t) 에 대하여 f1(t)⋅f2(t)⋅⋯⋅fk(t)f_1(t) \cdot f_2(t) \cdot \dots \cdot f_k(t) 는 T⁡\operatorname{T} 의 특성다항식이다.

  • 유한차원 벡터공간 V\mathbf{V} 가 주어지면 이 공간을 가능한 많은 T⁡\operatorname{T}-불변 부분공간의 직합으로 분해하는 것이 좋다. V\mathbf{V} 의 선형연산자 T⁡\operatorname{T} 의 행동을 직합을 구성하는 각각의 부분공간에서 추론할 수 있기 때문이다. 가령 T⁡\operatorname{T} 가 대각화가능한 것과 V\mathbf{V} 가 1차원 T⁡\operatorname{T}-불변 부분공간의 직합으로 완전히 분해되는 것은 동치이다.

  • T⁡\operatorname{T} 가 유한차원 벡터공간 V\mathbf{V} 의 대각화가능한 선형연산자이고 서로 다른 고윳값을 λ1,λ2,…,λk\lambda _1, \lambda _2, \dots, \lambda _k 로 두면 정리 5.10 에 의하여 V\mathbf{V} 는 T⁡\operatorname{T} 의 고유공간의 직합이다. 즉, V=⨁i=1kEλi\mathbf{V}= \displaystyle \bigoplus_{i=1}^{k}\mathbf{E}_{\lambda_i} 이다. 불변 부분공간 의 예시에서 고유공간은 T⁡\operatorname{T}-불변임을 증명했었다. 따라서 각 고유공간들은 정리 5.23 의 가정을 충족시킨다.

    정리 5.8 에 의하여 dim⁡(Eλi)=mi\dim (\mathbf{E}_{\lambda_i} ) = m_i 는 λi\lambda _i 의 중복도와 같다는 사실과 정리 5.6 에 의하여 T⁡\operatorname{T} 의 특성다항식 f(t)f(t) 은 스칼라 aa 에 대하여 다음과 같이 완전히 인수분해된다.

    f(t)=a∏i=1k(t−λi)mi f(t) = a \prod_{i=1}^{k}(t - \lambda _i) ^{m_i}

    우리가 이미 잘 알고 있었던 이 결과를 본 정리를 통하여 다시 도출해보자. 각 고윳값 λi\lambda _i 에 대하여 제한 T⁡Eλi\operatorname{T}_{\mathbf{E}_{\lambda_i} } 을 만들면 이것의 특성다항식은 (λi−t)mi(\lambda _i -t) ^{m_i} 이다. 본 정리에 의하여 T⁡\operatorname{T} 의 특성다항식은 다음과 같다.

    f(t)=(λ1−t)m1(λ2−t)m2…(λk−t)mk f(t) = (\lambda _1 - t) ^{m_1} (\lambda _2 - t) ^{m_2} \dots (\lambda _k - t) ^{m_k}

  • 증명

    T⁡\operatorname{T} 의 특성다항식을 f(t)f(t) 라고 하자.

    k=2k = 2 일 때 W1\mathbf{W}_1 의 순서기저를 β1\beta _1, W2\mathbf{W}_2 의 순서기저를 β2\beta _2 라 하고 β=b1∪b2\beta = b_1 \cup b_2 로 두자. 정리 5.9(4) 에 의하여 β\beta 는 V\mathbf{V} 의 순서기저이다. A=[T⁡]β,B1=[T⁡W1]β1,B2=[T⁡W2]β2A = [\operatorname{T}]_{\beta }, B_1 = [\operatorname{T}_{\mathbf{W}_1}]_{\beta _1}, B_2 = [\operatorname{T}_{\mathbf{W}_2}]_{\beta _2} 로 두면 정리 5.24 에 의하여 A=(B1OO′B2)A = \begin{pmatrix} B_1&O\\ O'&B_2\\ \end{pmatrix} 이다. 정리 5.20 의 증명과정에서처럼 f(t)f(t) 를 다음과 같이 전개할 수 있다.

    f(t)=det⁡(A−tI)=det⁡(B1−tI)det⁡(B2−tI)=f1(t)⋅f2(t) f(t) = \det(A - tI) = \det(B_1-tI) \det(B_2-tI) = f_1(t) \cdot f_2(t)

    따라서 k=2k=2 일 때 정리가 참이다. ▲

    k−1≥2k-1 \geq 2 인 k−1k-1 에 대하여 정리가 성립함을 가정하고 kk 에 대하여 성립함을 보이자. W=⨁i=1kWi\mathbf{W} = \displaystyle \bigoplus_{i=1}^{k}\mathbf{W}_i 로 두면 W\mathbf{W} 가 T⁡\operatorname{T}-불변이고 V=W⊕Wk\mathbf{V}= \mathbf{W}\oplus \mathbf{W}_k 임은 자명하다. k=2k = 2 일 때를 가정할 수 있으므로 T⁡W\operatorname{T}_{\mathbf{W}} 의 특성다항식 g(t)g(t) 에 대하여 f(t)=g(t)⋅fk(t)f(t) = g(t) \cdot f_k(t) 이다. k−1k-1 에서 정리가 성립하므로 g(t)=f1(t)⋅f2(t)⋅⋯⋅fk−1(t)g(t) = f_1(t) \cdot f_2(t) \cdot \dots \cdot f _{k-1}(t) 이다. 그러므로 다음이 성립한다.

    ∴f(t)=g(t)⋅fk(t)=f1(t)⋅f2(t)⋅⋯⋅fk(t)■ \therefore f(t) = g(t) \cdot f_k(t) = f_1(t) \cdot f_2(t) \cdot \dots \cdot f_k(t) \tag*{■}

    • 정리 5.23 은 드물게 이후의 정리인 5.24 를 기반으로 증명되는데, 5.24 가 5.23 을 가정하지 않으므로 순환논리가 되지는 않는다. 즉, 논리적으로 문제는 없다.

    • 원래 증명에서는 W=∑i=1k−1Wi\mathbf{W} = \displaystyle \sum_{i=1}^{k-1}\mathbf{W}_i 로 두는데 V=⨁i=1kWi\mathbf{V}= \displaystyle \bigoplus_{i=1}^{k}\mathbf{W}_i 라는 가정이 i,j∈{1,…,k−1}i, j \in \{1, \dots, k-1\} 에 대하여 Wj∩∑i≠jWi={0}\mathbf{W}_j \cap \displaystyle \sum_{i \neq j}\mathbf{W}_i = \{0\} 를 함의한다고 생각해서 그냥 W=⨁i=1k−1Wi\mathbf{W} = \displaystyle \bigoplus_{i=1}^{k-1}\mathbf{W}_i 로 바꿨다.

  • 예시

    R4\R ^{4} 의 선형연산자 T⁡(a,b,c,d,)=(2a−b,a+b,c−d,c+d)\operatorname{T}(a,b,c,d,) = (2a-b,a+b,c-d,c+d) 와 W1={(s,t,0,0):s,t∈R},W2={(0,0,s,t):s,t∈R}\mathbf{W}_1=\{(s,t,0,0) : s,t \in \R\}, \mathbf{W}_2=\{(0,0,s,t) : s,t \in \R\} 를 정의하면 W1,W2\mathbf{W}_1, \mathbf{W}_2 는 T⁡\operatorname{T}-불변이고 R4=W1⊕W2\R ^{4}= \mathbf{W}_1 \oplus \mathbf{W}_2 이다. β1={e1,e2},β2={e3,e4},β=β1∪β2\beta _1=\{e_1,e_2\},\beta _2=\{e_3,e_4\},\beta =\beta_1 \cup \beta _2 로 두고 각각을 W1,W2,R4\mathbf{W}_1, \mathbf{W}_2, \R ^{4} 의 순서기저로 두자. A=[T⁡]β,B1=[T⁡W1]β1,B2=[T⁡W2]β2A = [\operatorname{T}]_{\beta }, B_1 = [\operatorname{T}_{\mathbf{W}_1}]_{\beta _1}, B_2= [\operatorname{T}_{\mathbf{W}_2}]_{\beta _2} 는 다음과 같다.

    B1=(2−111),B2=(1−111),A=(B1OOB2)=(2−1001100001−10011) B_1 = \begin{pmatrix} 2&-1\\ 1&1\\ \end{pmatrix}, B_2 = \begin{pmatrix} 1&-1\\ 1&1\\ \end{pmatrix}, A = \begin{pmatrix} B_1&O\\ O&B_2\\ \end{pmatrix} = \begin{pmatrix} 2&-1&0&0\\ 1&1&0&0\\ 0&0&1&-1\\ 0&0&1&1\\ \end{pmatrix}

    T⁡\operatorname{T} , T⁡W1\operatorname{T}_{\mathbf{W}_1} , T⁡W2\operatorname{T}_{\mathbf{W}_2} 의 특성다항식을 f(t),f1(t),f2(t)f(t),f_1(t),f_2(t) 로 두면 다음이 성립한다.

    f(t)=det⁡(A−tI)=det⁡(B1−tI)det⁡(B2−tI)=f1(t)⋅f2(t) f(t) = \det(A-tI) =\det(B_1-tI) \det(B_2-tI) =f_1(t) \cdot f_2(t)

두 행렬의 직합(direct sum of two matrices)

B1∈Fm×m,B2∈Fn×nB_1 \in \mathbf{F}^{m \times m}, B_2 \in \mathbf{F}^{n \times n} 에 대하여 B1,B2B_1, B_2 의 직합은 다음과 같은 (m+n)×(m+n)(m + n) \times (m + n) 행렬 AA 로 정의하고 B1⊕B2B_1 \oplus B_2 로 표기한다.

Aij={(B1)ij1≤i,j≤m(B2)(i−m),(j−m)m+1≤i,j≤n+m0 otherwise  A _{ij} = \begin{cases} (B_1) _{ij} & 1 \leq i, j \leq m\\ (B_2) _{(i-m),(j-m)} & m+1 \leq i, j \leq n+m\\ 0 & \text{ otherwise }\\ \end{cases}
  • 즉, 적절한 영행렬 OO 에 대하여 A=B1⊕B2=(B1OOB2)A = B_1 \oplus B_2 = \begin{pmatrix} B_1&O\\ O&B_2\\ \end{pmatrix} 라고 정의하는 것이다.

행렬의 직합(direct sum of matrices)

정사각행렬 B1,B2,…,BkB_1, B_2, \dots, B_k 에 대하여 B1,B2,…,BkB_1, B_2, \dots, B_k 의 직합은 재귀적으로 ⨁i=1kBi=(⨁i=1k−1Bi)⊕Bk\displaystyle \bigoplus_{i=1}^{k}B_i = \bigg (\bigoplus_{i=1}^{k-1}B_i\bigg ) \oplus B_k 라 정의한다.

  • 즉, 적절한 영행렬 OO 에 대하여 A=⨁i=1kBiA = \displaystyle \bigoplus_{i=1}^{k}B_i 를 다음과 같이 정의하는 것이다.

    A=⨁i=1kBi=(B1O…OOB2…O⋮⋮⋱⋮OO…Bk) A = \displaystyle \bigoplus_{i=1}^{k}B_i = \begin{pmatrix} B_1&O&\dots&O\\ O&B_2&\dots&O\\ \vdots& \vdots& \ddots& \vdots \\ O&O&\dots&B_k\\ \end{pmatrix}

  • 예시

    정사각행렬 B1=(1211),B2=(3),B3=(121123111)B_1 = \begin{pmatrix} 1&2\\ 1&1\\ \end{pmatrix}, B_2 = (3), B_3 = \begin{pmatrix} 1&2&1\\ 1&2&3\\ 1&1&1\\ \end{pmatrix} 에 대하여 B1⊕B2⊕B3B_1 \oplus B_2 \oplus B_3 는 다음과 같다.

    ⨁i=13Bi=(120000110000003000000121000123000111) \bigoplus_{i=1}^{3}B_i = \begin{pmatrix} 1&2&0&0&0&0\\ 1&1&0&0&0&0\\ 0&0&3&0&0&0\\ 0&0&0&1&2&1\\ 0&0&0&1&2&3\\ 0&0&0&1&1&1\\ \end{pmatrix}

정리 5.24

유한차원 벡터공간 V\mathbf{V} 의 선형연산자 T⁡\operatorname{T} 와 V=⨁i=1kWi\mathbf{V}= \displaystyle \bigoplus_{i=1}^{k}\mathbf{W}_i 인 T⁡\operatorname{T}-불변 부분공간 W1,W2,…,Wk\mathbf{W}_1, \mathbf{W}_2, \dots, \mathbf{W}_k 에 대하여 각 ii 에 대한 βi\beta _i 는 Wi\mathbf{W}_i 의 순서기저이고 β=⋃i=1kβi\beta = \displaystyle \bigcup_{i=1}^{k}\beta _i 라고 하고 A=[T⁡]β,Bi=[T⁡Wi]βiA = [\operatorname{T}]_{\beta }, B_i = [\operatorname{T}_{\mathbf{W}_i}]_{\beta _{i}} 라고 하면 다음이 성립한다.

A=⨁i=1kBi A = \bigoplus_{i=1}^{k} B_i

  • 이 정리가 하는 역할은 행렬의 직합을 불변 부분공간의 직합과 연관짓는것이다.

  • 증명

    k=2k = 2 를 가정하자.

    문제 5.4-12 의 증명과정은 T⁡\operatorname{T}-불변 부분공간의 순서기저로 이루어진 V\mathbf{V} 의 기저로 T⁡\operatorname{T} 를 행렬표현하면 T⁡\operatorname{T}-불변의 기저로 표현된 열들이 반드시 T⁡\operatorname{T}-불변의 기저로만 표현되어야 함을 말해준다. 즉, β1={v1,…,vs},β2={vs+1,…,vt}\beta _1 = \{v_1, \dots, v_s\}, \beta _2 = \{v _{s+1}, \dots, v_t\} 를 가정하면 β=β1∪β2\beta = \beta _1 \cup \beta _2 는 V\mathbf{V} 의 순서기저가 되고 A=[T⁡]βA = [\operatorname{T}]_{\beta } 는 다음과 같다.

    T⁡(v1)=∑i=1sai1v1 \operatorname{T}(v_1) = \sum_{i=1}^{s}a _{i1}v_1
    ⋮ \vdots
    T⁡(vs)=∑i=1saisvs \operatorname{T}(v_s) = \sum_{i=1}^{s}a _{is}v_s
    T⁡(vs+1)=∑i=s+1⊤ai,s+1vs+1 \operatorname{T}(v _{s+1}) = \sum_{i=s+1}^{\top}a _{i,s+1}v _{s+1}
    ⋮ \vdots
    T⁡(vt)=∑i=t⊤aitvt \operatorname{T}(v _{t}) = \sum_{i=t}^{\top}a _{it}v _{t}
    ⟹A=(B1OOB2) \implies A = \begin{pmatrix} B_1&O\\ O&B_2\\ \end{pmatrix}

    이는 A=B1⊕B2A = B_1 \oplus B_2 을 뜻한다. ▲

    k−1k-1 에서 정리가 성립함을 가정하고 kk 에 대하여 성립함을 보이자. W=⨁i=1k−1Wi\mathbf{W}=\displaystyle \bigoplus_{i=1}^{k-1}\mathbf{W}_i 에 대하여 β′=⋃i=1k−1βi\beta ' = \displaystyle \bigcup_{i=1}^{k-1}\beta _i 로 두면 다음이 성립한다.

    [T⁡W]β′=⨁i=1k−1Bi=B′ [\operatorname{T}_{\mathbf{W}}]_{\beta '} = \bigoplus_{i=1}^{k-1}B_i = B'

    문제 5.4-12 의 증명과정은 T⁡\operatorname{T}-불변 부분공간의 순서기저로 이루어진 V\mathbf{V} 의 기저로 T⁡\operatorname{T} 를 행렬표현하면 T⁡\operatorname{T}-불변의 기저로 표현된 열들이 반드시 T⁡\operatorname{T}-불변의 기저로만 표현되어야 함을 말해준다. 즉, β′={v1,…,vs},βk={vs+1,…,vt}\beta ' = \{v_1, \dots, v_s\}, \beta _k = \{v _{s+1}, \dots, v_t\} 를 가정하면 β=β′∪βk\beta = \beta ' \cup \beta _k 는 V\mathbf{V} 의 순서기저가 되고 A=[T⁡]βA = [\operatorname{T}]_{\beta } 는 다음과 같다.

    T⁡(v1)=∑i=1sai1v1 \operatorname{T}(v_1) = \sum_{i=1}^{s}a _{i1}v_1
    ⋮ \vdots
    T⁡(vs)=∑i=1saisvs \operatorname{T}(v_s) = \sum_{i=1}^{s}a _{is}v_s
    T⁡(vs+1)=∑i=s+1⊤ai,s+1vs+1 \operatorname{T}(v _{s+1}) = \sum_{i=s+1}^{\top}a _{i,s+1}v _{s+1}
    ⋮ \vdots
    T⁡(vt)=∑i=t⊤aitvt \operatorname{T}(v _{t}) = \sum_{i=t}^{\top}a _{it}v _{t}
    ⟹A=(B′OOBk) \implies A = \begin{pmatrix} B'&O\\ O&B_k\\ \end{pmatrix}

    이는 A=B′⊕BkA = B' \oplus B_k 을 뜻한다. B′=⨁i=1k−1Bi\displaystyle B' = \bigoplus_{i=1}^{k-1}B_i 이므로 다음이 성립한다.

    ∴A=(⨁i=1k−1Bi)⊕Bk=⨁i=1kBi■ \therefore A = \bigg (\bigoplus_{i=1}^{k-1}B_i\bigg ) \oplus B_k = \bigoplus_{i=1}^{k}B_i \tag*{■}
        Friedberg, S. H., Insel, A. J., & Spence, L. E. (2018). Linear algebra. Pearson.