Derivative

Derivative✔

• \(\Delta x = b - a\) 와 \(\Delta y = f(b) - f(a)\) 로 두고 다음과 같이 표기할 수도 있다. 이때 \(\Delta\) 는 "~의 변화"를 뜻한다.

  \[ \frac{\Delta y}{\Delta x} = \frac{f(b)-f(a)}{b-a} = \frac{f(a+\Delta x)-f(a)}{\Delta x} \]

• 평균변화율이란 \(x \in X\) 가 \(a\) 에서 \(b\) 까지 변할 때의 \(y \in Y\) 가 \(\frac{\Delta y}{\Delta x}\) 만큼 변한다는 의미이다.

• 평균변화율은 기하학적으로 \(y = f(x)\) 위의 두 점 \((a,f(a)),(b,f(b))\) 를 지나는 직선의 기울기이다.

• 예시

  함수 \(f(x) = x^2 + 2\) 에 대하여 \(x\) 값이 \(0\) 에서 \(2\) 로 변할 때 평균변화율을 다음과 같다.

  \[ \frac{\Delta y}{\Delta x} = \frac{f(2) - f(0)}{2 - 0} = \frac{(2^2+2)-2}{2} = 2 \]

  이는 \(x\) 가 \(1\) 변할 때 \(y\) 가 평균적으로 \(2\) 변했다는 뜻이다.

• \(\Delta x = x - c\) 로 두고 다음과 같이 표기할 수도 있다. 이때 \(\Delta\) 는 "~의 변화"를 뜻한다.

  \[ f'(c) = \lim_{\Delta x \to 0} \frac{f(\Delta x + c) - f(c)}{\Delta x} \]

  일반적으로 \(\Delta x = h\) 로 더욱 간단히 표기하여 다음과 같이 표기하는 것이 일반적이다.

  \[ f'(c) = \lim_{h \to 0} \frac{f(h + c) - f(c)}{h} \]

• \(c\) 에서 미분가능한 함수 \(f\) 에 대한 \(f'(c)\) 는 \(\dfrac{df}{dx}(c)\) 라고도 표기한다. \(dx\) 란 \(x\) 의 무한히 작은 변화량을 뜻한다.

• 함수 \(y = f(x)\) 의 \(x\) 에 대한 미분은 변수 \(x\) 가 변할 때 변수 \(y\) 가 변하는 변화율을 측정하는 도구이다. 따라서 이 경우 미분은 그래프의 각 지점에서의 기울기를 의미한다.

  

  위와 같은 선형 함수의 경우 \(x\) 가 변할 때 변수 \(y\) 가 변하는 변화율이 일정하다. 그래서 이 함수의 미분계수는 상수로 일정하다. 위 그림에서 선형 함수 \(y = f(x) = mx + b\) 의 기울기는 다음과 같이 표현된다.

  \[ m = \dfrac{\Delta y}{\Delta x} \]

  "\(\Delta x\)" 라는 표현은 "\(x\)에서의 변화" 라고 읽으면 된다.

  만약 그래프가 선형이 아닐 경우 각각의 지점에서 \(\Delta x\) 가 \(0\) 으로 수렴할 때의 \(\dfrac{\Delta y}{\Delta x}\) 를 미분값으로 구하게 된다.

  

  위 그림은 \(x\) 가 \(x + h\) 까지 변할 때의 평균변화율을 측정한다. 이때 \(\Delta x = x + h - x = h\) 이다.

  

  그러나 위 그림은 \(h \to 0\) 로 보내서 \(\Delta x\) 가 \(0\) 로 수렴할 때의 순간변화율을 측정한다. 이것이 미분계수가 된다.

• 예시

  \(f(x) = x ^{n}\) 의 \(c \in \R\) 에서 미분계수를 구해보자. 미분계수의 정의에 의하여 다음이 성립한다.

  \[ \begin{align}\begin{split} f'(c) = \lim_{x \to c} \dfrac{x ^{n} - c ^{n}}{x - c}&= \lim_{x \to c} \dfrac{(x - c)(x ^{n-1} + c x ^{n-2} + \dots + c ^{n-1})}{x - c} \\ &=\lim_{x \to c} (x ^{n-1} + c x ^{n-2} + \dots + c ^{n-1}) = n c ^{n-1} \\ \end{split}\end{align} \tag*{} \]

• 예시

  \(g(x) = |x|\) 의 \(c = 0\) 의 미분계수는 \(g'(0) = \displaystyle \lim_{x \to 0} \dfrac{|x| }{x}\) 인데 우극한과 좌극한이 각각 \(+1\) 과 \(-1\) 로 서로 다르므로 정리 4.6.3 에 의하여 미분불가능하다.

• \(y - x = \Delta x\) 로 두고 다음과 같이 표기할 수 있다.

  \[ f'(x) = \lim_{\Delta x \to 0} \frac{f(\Delta x + x) - f(x)}{\Delta x} \]

  이때 \(\Delta x = h\) 로 간단히 표현해서 다음과 같이 편하게 표기하는 것이 일반적이다.

  \[ f'(x) = \lim_{h \to 0} \frac{f(h + x) - f(x)}{h} \]

• 도함수를 구하는 과정인 미분(differentiation)을 정의역에서 미분가능한 함수 집합을 정의역으로 갖고, 공역을 함수 집합으로 갖는 연산자 \(D\) 로 정의할 수 있다. 그러면 미분가능한 함수 \(f\) 에 대하여 \(D(f) = f'\) 로 쓸 수 있다.

• 도함수를 미분이라는 용어로 사용하면 derivative 이고, 도함수를 구하는 과정 자체를 미분이라는 용어로 사용하면 differentiation 이다. 영어에서는 이렇게 derivative 와 differentiation 을 구별하지만 한글에서는 미분이라는 용어가 다양하게 사용되니 주의해야 한다.

• 함수 \(y = f(x)\) 를 미분할 때 수학자들마다 다양한 표기법을 사용했다.

• 라이프니츠 표기법

  \(y = f(x)\) 를 \(x\) 에 대하여 미분할 때 다음과 같이 표기한다. \(x\) 가 변할 때(\(dx\)) \(y\) 가 변하는(\(dy\)) 변화율(\(dy/dx\))을 표현한 것이다. \(dx\) 를 "\(x\) 의 무한히 극미한 변화량" 으로 읽으면 된다. 한 없이 \(0\) 에 가까워지는 \(\Delta x\) 를 \(dx\) 로 표현한다고 보면 된다. 그래서 \(\displaystyle \lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x} = \dfrac{dy}{dx}\) 로 표현하는 것이다.

  \[ \frac{dy}{dx}, \quad \frac{df}{dx}, \quad \frac{d}{dx}f \]

  이계도함수는 다음과 같이 표기한다.

  \[ \frac{d}{dx}\bigg (\frac{dy}{dx} \bigg ) = \dfrac{d ^{2}y}{dx ^{2}} \]

  \(n\)계도 함수는 다음과 같이 표기한다.

  \[ \dfrac{d ^{n}y}{dx ^{n}}, \quad \dfrac{d ^{n} f}{dx ^{n}}, \quad \dfrac{d ^{n}}{dx ^{n}}f \]

  라이프니츠의 표기법에서 특정한 점 \(x = a\) 에서의 미분계수는 다음과 같이 표기한다.

  \[ \dfrac{dy}{dx}\bigg |_{x = a} = \frac{dy}{dx}(a) \]

• 라그랑주 표기법(prime notation)

  라그랑주는 함수 \(f\) 의 미분을 \(f'\) 로 표기했다. 고차 미분은 다음과 같이 표기했다.

  \[ (f')', \quad (f'')' = f''' \]

  이 표기법은 프라임 기호(\('\))를 여러번 쓸 수 없어서 \(f^{(n)}\) 로 발전했다. 가령 4번 미분하면 \(f^{(4)}\) 로 표기한다.

• 오일러 표기법

  오일러는 미분 연산자 \(D\) 를 함수 \(f\) 에 적용한다는 의미로 \(f\) 의 도함수를 \(Df\) 로 썼다. \(n\)계도 함수는 \(D ^{n}f\) 로 표기한다.

  \(y = f(x)\) 에서 독립변수 \(x\) 에 \(y\) 가 의존하면 독립변수 \(x\) 를 표기하기 위하여 \(D _{x}y\) 와 같이 표기했다. 그러나 이 경우 변수가 \(x\) 밖에 없는 일변수함수인 자명한 상황이기 때문에 \(x\) 를 생략하여 \(Dy\) 또는 \(Df(x)\) 로 표기한다.

Differentiable and Continuity✔

• 함수가 연속이라고 해서 미분가능한 것은 아니다. 다음과 같이 \(y = |x|\) 는 연속이지만 \(0\) 에서 미분불가능하다.

  

  그러나 이 정리는 미분가능이면 연속임을 말해준다.

• 증명

  \(g\) 가 \(c\) 에서 미분가능하면 극한값 \(\displaystyle g'(c) = \lim_{x \to c} \frac{g(x) - g(c)}{x - c}\) 가 존재한다. 이를 기반으로 \(\displaystyle \lim_{x \to c} g(x) = g(c)\) 를 증명하면 정리 4.3.2에 의하여 증명이 끝난다. 함수의 극한과 사칙연산에 의하여 다음이 성립한다.

  \[ \lim_{x \to c} (g(x) -g(c)) = \lim_{x \to c} \bigg (\frac{g(x) - g(c)}{x - c} \bigg )(x - c) = g'(c) \cdot 0 = 0 \]

  이는 \(\lim_{x \to c} g(x) = g(c)\) 을 뜻한다. ■

Differentiability classes✔

• \(C ^{k}\) 집합은 \(C ^{k+1}\) 집합을 진부분집합으로 가진다. 즉, 다음이 성립한다.

  \[ C ^{0} \supsetneq C ^{1} \supsetneq \dots \supsetneq C ^{k} \supsetneq C ^{k+1} \supsetneq \dots \supsetneq C ^{\infty } \supsetneq C ^{\omega }\]

• 미분가능한 함수는 다음과 같이 국소적으로 선형근사 가능하다.

  

Combinations of Differentiable Functions✔

• 곱함수를 \(fg\) 라고 표기하고 합성함수를 \(f \circ g\) 라고 표기한다. 3) 의 \((fg)'(c)\) 는 합성함수의 미분법이 아니라 곱의 미분법이다.

• 증명

  1:

  함수의 극한과 사칙연산에 의하여 다음이 성립한다.

  \[ \begin{align}\begin{split} (f + g)'(c)&= \lim_{x \to c} \dfrac{(f + g)(x) - (f + g)(c)}{x - c} \\ &= \lim_{x \to c} \dfrac{f(x) - f(c) + g(x) - g(c)}{x - c} \\ &=\lim_{x \to c} \dfrac{f(x) - f(c)}{x - c} + \lim_{x \to c} \dfrac{ g(x) - g(c)}{x - c} = f'(c) + g'(c) \end{split}\end{align} \tag*{} \]

  ■

  2:

  함수의 극한과 사칙연산에 의하여 쉽게 증명할 수 있다.

  3:

  먼저 다음이 성립한다.

  \[ \begin{align}\begin{split} \dfrac{(fg)(x) - (fg)(c)}{x - c} & = \dfrac{f(x)g(x) - f(x)g(c) + f(x)g(c) - f(c)g(c)}{x - c} \\ &= f(x)\frac{g(x)-g(c)}{x-c} + g(c) \frac{f(x) - f(c)}{x - c} \\ \end{split}\end{align} \tag*{} \]

  \(f\) 는 \(c\) 에서 미분가능하므로 정리 5.2.3 에 의하여 \(c\) 에서 연속이고 정리 4.3.2 에 의하여 \(\displaystyle \lim_{x \to c} f(x) = f(c)\) 이다. 그러면 함수의 극한과 사칙연산에 의하여 다음이 성립한다.

  \[ \lim_{x \to c} \dfrac{(fg)(x) - (fg)(c)}{x - c} = f(c)g'(c) + f'(c)g(c) \]

  ■

  4:

  먼저 다음이 성립한다.

  \[ \begin{align}\begin{split} \dfrac{(f/g)(x) - (f/g)(c)}{x - c}&= \frac{1}{x- c}\bigg (\frac{f(x)}{g(x)} - \frac{f(c)}{g(c)} \bigg ) = \frac{1}{x-c}\bigg (\frac{f(x)g(c) - f(c)g(x)}{g(x)g(c)} \bigg ) \\ &= \frac{1}{x - c}\bigg ( \frac{f(x)g(c) - f(c)g(c) + f(c)g(c) - f(c)g(x)}{g(x)g(c)}\bigg ) \\ &= \frac{1}{g(x)g(c)}\bigg ( g(c)\frac{f(x)-f(c)}{x-c} - f(c) \frac{g(x) - g(c)}{x-c} \bigg ) \end{split}\end{align} \tag*{} \]

  따라서 다음이 성립한다.

  \[ \bigg (\frac{f}{g} \bigg )'(c) = \frac{1}{[g(c)]^{2}}(g(c)f'(c) - f(c)g'(c)) \]

  ■

Chain Rule✔

• 증명

  합성함수 \(g \circ f\) 의 미분계수를 다음과 같이 구할 수 있다.

  \[ (g \circ f)'(c) = \lim_{x \to c} \dfrac{g(f(x)) - g(f(c))}{x - c} \]
  \[ = \lim_{x \to c} \frac{g(f(x)) - g(f(c))}{f(x) - f(c)} \cdot \frac{f(x) - f(c)}{x - c} = g'(f(c)) \cdot f'(c) \]

  그러나 임의의 근방 \(V_{\epsilon}(c)\) 에 속하는 \(x \in V_{\epsilon}(c)\) 에 대하여 \(f(x) = f(c)\) 이면 분모가 \(0\) 이 된다. 그러면 극한값이 정의되지 않고, 결국 미분계수도 존재하지 않아 미분 불가능하다는 것인가? 그렇지 않다. 이 문제를 해결해보자. ▲

  일단 \(g\) 가 \(f(c)\) 에서 미분가능하므로 다음 극한값이 존재한다.

  \[ g'(f(c)) = \lim_{y \to f(c)} \frac{g(y) - g(f(c))}{y - f(c)} \]

  이때 다음과 같은 함수를 정의하자.

  \[ d(y) = \dfrac{g(y) - g(f(c))}{y - f(c)} \tag{1} \]

  그러면 \(\displaystyle \lim_{y \to f(c)} d(y) = g'(f(c))\) 이다. \(d(y)\) 에서 \(y = f(c)\) 이면 분모가 \(0\) 이 되므로 정의되지 않지만, \(y = f(c)\) 인 경우에는 \(d(y)\) 를 \((1)\) 로 정의하는 것이 아니라 \(d(f(c)) = g'(f(c))\) 로 정의하자.

  그러면 \(\displaystyle \lim_{y \to f(c)} d(y) = g'(f(c)) = d(f(c))\) 이므로 정리 4.3.2에 의하여 \(d(y)\) 는 \(f(c)\) 에서 연속이다. ▲

  \(y \neq f(c)\) 일 때 \((1)\) 이 성립하는데 \((1)\) 은 다음과 같이 쓸 수 있다.

  \[ g(y) - g(f(c)) = d(y)(y - f(c)) \tag{2} \]

  그런데 이 식은 \(y = f(c)\) 일 때에도 성립한다. 따라서 \((2)\) 는 임의의 \(x \in A\) 에 대한 \(y = f(x)\) 에 대하여서도 성립한다.

  그러면 \(x \neq c\) 인 \(x\) 에 대하여 \((2)\) 를 \(x - c\) 로 나누면 다음이 성립한다.

  \[ \frac{g(f(x)) - g(f(c))}{x - c} = d(f(x)) \cdot \frac{f(x) - f(c)}{x - c} \]

  여기에 \(x \to c\) 의 극한을 취하면 함수의 극한과 사칙연산에 의하여 다음이 성립한다.

  \[ \begin{align}\begin{split} (g \circ f)'(c) &= \lim_{x \to c} \frac{g(f(x)) - g(f(c))}{x - c} \\ &= \lim_{x \to c} \bigg \{ d(f(x)) \cdot \frac{f(x) - f(c)}{x - c} \bigg \}\\ &= \lim_{y \to f(c)} d(y) \cdot \lim_{x \to c} \frac{f(x) - f(c)}{x - c} = g'(f(c)) \cdot f'(c)\\ \end{split}\end{align} \tag*{} \]

  즉, \(g \circ f\) 의 \(c\) 에서의 미분계수가 존재하므로 \(c\) 에서 미분가능하고, 그 값은 정리의 결론대로 증명되었다. ■

Interior Extremum Theorem✔

• 이 정리는 미분가능한 함수의 최댓값과 최솟값은 미분계수가 \(0\) 이라는 것을 말해준다.

  

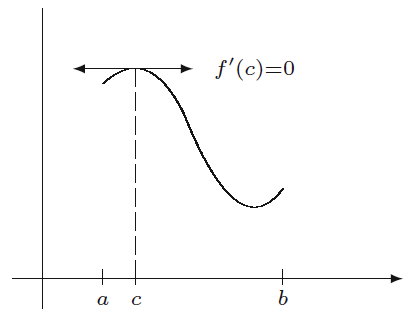
• 증명

  1:

  \(c\) 가 열린 구간 \((a, b)\) 에 속해 있으므로 모든 \(n \in \N\) 에 대하여 \(x_n < c < y_n\) 이면서 \(c\) 로 수렴하는 수열 \((x_n), (y_n) \subset (a, b)\) 이 존재한다. \(f(c)\) 가 최대값이므로 모든 \(n\) 에 대하여 \(f(y_n) - f(c) \leq 0\) 이고 극한과 부등식에 의하여 다음이 성립한다.

  \[ f'(c) = \lim_{n \to \infty} \frac{f(y_n) - f(c)}{y_n - c} \leq 0 \]

  같은 논리로 \(x_n\) 에 대한 부등식도 취할 수 있는데 \((x_n)\) 에 대해서는 \(x_n - c \leq 0\) 이므로 다음이 성립한다.

  \[ f'(c) = \lim_{n \to \infty} \frac{f(x_n) - f(c)}{x_n - c} \geq 0 \]

  따라서 \(f'(c) = 0\) 이다. ■

  2:

  1) 을 증명한 논리와 같은 논리로 쉽게 증명할 수 있다. ■

Darboux's theorem✔

• 이 정리는 도함수는 사잇값 성질을 만족한다는 것을 말해준다. 만약 도함수가 서로 다른 값 \(f'(a)\) 와 \(f'(b)\) 를 가지면 그 사이 모든 값을 함수값으로 가진다. 이로써 도함수는 불연속일 수도 있지만 사잇값 성질은 반드시 만족한다.

• 그런데 연속함수는 반드시 사잇값 성질을 만족한다. 그러므로 모든 연속함수는 어떤 함수의 도함수이다. 이로써 도함수 집합은 적어도 연속함수를 포함하지만, 도함수 집합을 간결하게 특정하는 일은 지금도 성공적이지 못하다.

• 증명

  \([a, b]\) 에서 새로운 함수 \(g(x) = f(x) - \alpha x\) 를 정의하면 \(g\) 는 \([a, b]\) 에서 미분가능하고 \(g'(x) = f'(x) - \alpha\) 이다. 그러면 \(g'(a) < 0 < g'(b)\) 일 때 어떤 \(c \in (a, b)\) 에 대하여 \(g'(c) = 0\) 임을 보이면 된다. ▲

  먼저 \(g(x) < g(a)\) 를 만족하는 \(x \in (a, b)\) 가 존재함을 보이자. \(a\) 로 수렴하는 수열 \((x_n) \subset (a, b)\) 에 대하여 다음이 성립한다.

  \[ g'(a) = \lim_{n \to \infty} \dfrac{g(x_n) - g(a)}{x_n - a} < 0 \]

  분모는 반드시 양수다. 분자가 음수가 아니면 극한과 부등식에 의하여 모순이므로 분자는 음수이다. 따라서 \(a\) 와 가까운 어떤 점 \(x \in (a, b)\) 가 존재하여 \(g(a) > g(x)\) 를 만족시킨다. 마찬가지의 이유로 \(b\) 와 가까운 어떤 점 \(y \in (a, b)\) 가 존재하여 \(g(y) < g(b)\) 를 만족시킨다. ▲

  이제 어떤 점 \(c \in (a, b)\) 가 \(g'(c) = 0\) 를 만족시킨다는 것을 보이자. 먼저 닫힌 구간은 콤팩트하므로 \([a, b]\) 은 콤팩트하다. 또한 \(g\) 가 \([a, b]\) 에서 미분가능하므로 \(g\) 는 \([a, b]\) 에서 연속이다. 그러면 최대-최소 정리에 의하여 \(g\) 는 어떤 점 \(c \in (a, b)\) 에서 최소값을 갖는다.

  위의 논의에 의하여 \(g(a)\) 와 \(g(b)\) 는 항상 어떤 점보다 크므로 둘 다 최솟값이 아니다. 그러면 페르마의 정리에 의하여 \(g'(c) = 0\) 이고, \(c \in (a, b)\) 이며, 다음이 성립한다.

  \[ g'(c) = 0 \implies f'(c) = \alpha \]

  ■

Mean Value Theorem✔

Rolle's theorem✔

• 롤의 정리는 평균값 정리의 특수한 경우이다.

• 롤의 정리의 기하학적 의미는 다음과 같이 구간의 최솟값과 최댓값이 같을 때 미분계수가 \(0\) 인 점 \(c\) 가 존재한다는 것이다.

  

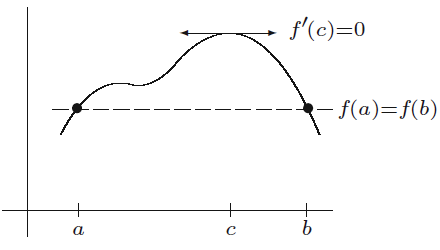
• 증명

  닫힌 구간은 콤팩트하므로 \([a, b]\) 은 콤팩트하다. 또한 \(f\) 가 \([a, b]\) 에서 연속이므로 최대-최소 정리에 의하여 \(f\) 는 최댓값과 최솟값을 갖는다.

  \(a\) 와 \(b\) 가 최댓값과 최솟값이 되면 \(f\) 는 상수함수가 되고 \((a, b)\) 전체에서 \(f'(x) = 0\) 이 된다. 이 경우 \(c\) 의 존재성은 자명하다. ▲

  \(f\) 가 \((a, b)\) 내부의 어떤 점 \(c\) 에서 최댓값 또는 최솟값을 가지면 페르마의 정리에 의하여 \(f'(c) = 0\) 이다. ■

Mean Value Theorem✔

• 즉, 평균값 정리는 구간 \([a, b]\) 에서 미분가능한 함수 \(f\) 에 대한 양 끝점 \((a, f(a)), (b, f(b))\) 를 잇는 직선의 기울기와 기울기가 같은 접선의 존재성을 보장해준다. 다음 그림은 평균값 정리의 기하학적 의미를 바로 보여준다.

  

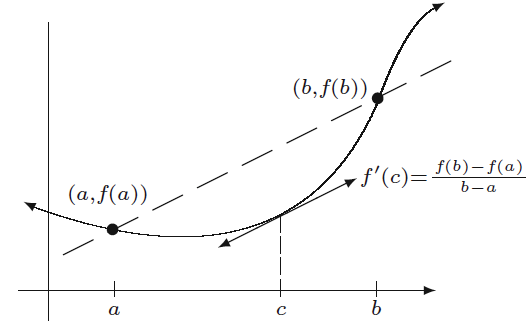
• 이 정리에서 \(f(a) = f(b)\) 인 경우가 롤의 정리이다.

• 증명

  두 점 \((a, f(a)), (b, f(b))\) 를 지나는 직선의 방정식은 다음과 같다.

  \[ y = \bigg (\frac{f(b) - f(a)}{b - a} \bigg )(x - a) + f(a) \]

  이 직선과 \(f(x)\) 의 차이를 나타내는 함수를 다음과 같이 정의하자.

  \[ d(x) = f(x) - \bigg \{ \bigg (\frac{f(b) - f(a)}{b - a} \bigg )(x - a) + f(a) \bigg \}\]

  연속성과 사칙연산에 의하여 \(d\) 는 \([a, b]\) 에서 연속이다. 또한 \(d\) 는 \((a, b)\) 에서 미분가능하고 \(d(a) = 0 = d(b)\) 이다. 그러면 롤의 정리에 의하여 \(d'(c) = 0\) 인 점 \(c \in (a, b)\) 가 존재한다. 이때 \(d'(x)\) 는 다음과 같다.

  \[ d'(x) = f'(x) - \dfrac{f(b) - f(a)}{b - a} \]

  \(d'(c) = 0 = f'(c) - \dfrac{f(b) - f(a)}{b - a}\) 이므로 증명이 끝났다. ■

• 이 정리는 모든 미분계수가 \(0\) 이면 그 함수는 상수함수임을 말해준다. 상수함수의 도함수가 \(0\) 임은 자명하지만, 이 정리는 그 역을 증명한 것이다.

• 증명

  \(x < y\) 인 임의의 \(x, y \in A\) 에 대하여 구간 \([x ,y]\) 에서 \(g\) 에 대하여 평균값 정리를 적용하면 다음을 만족하는 \(c \in A\) 가 존재한다.

  \[ g'(c) = \dfrac{g(y) - g(x)}{y - x} \]

  \(g'(c) = 0\) 이므로 \(g(y) = g(x)\) 이다. 이 값을 \(k\) 라고 하자. \(x, y\) 를 임의로 선택했으므로 \(\forall x \in A : g(x) = k\) 이다. ■

• 증명

  함수 \(h(x) = f(x) - g(x)\) 를 정의하면 \(\forall x \in A : h'(x) = 0\) 이다. 따름정리 5.3.3 에 의하여 \(h(x) = k = f(x) - g(x)\) 이다. ■

Generalized Mean Value Theorem✔

• GMVT 라고도 부른다.

• 증명

  함수 \(h\) 를 다음과 같이 정의하자.

  \[ h(x) = [f(b) - f(a)]g(x) - [g(b) - g(a)]f(x) \]

  연속성과 사칙연산에 의하여 \(h\) 는 \([a, b]\) 에서 연속이고, 정리 5.2.4 에 의하여 \(h\) 는 \((a, b)\) 에서 미분가능하다. 또한 다음이 성립한다.

  \[ h(a) = g(a)f(b) - f(a)g(b) = h(b) \]

  그러면 롤의 정리에 의하여 \(h'(c) = 0\) 인 \(c \in (a, b)\) 가 존재한다. \(h'(x)\) 에 \(c\) 를 대입하면 다음이 성립한다.

  \[ h'(x) = [f(b) - f(a)]g'(x) - [g(b) - g(a)]f'(x) \implies \]
  \[ [f(b) - f(a)]g'(c) - [g(b) - g(a)]f'(c) = 0 \]

  ■

L'Hospital's Rules✔

• 증명

  임의의 양수 \(\epsilon\) 와 어떤 실수 \(L\) 에 대하여 \(L = \displaystyle \lim_{x \to a} \frac{f'(x)}{g'(x)}\) 이므로 함수의 극한에 의하여 다음을 만족시키는 \(\delta\) 가 존재한다.

  \[ 0 < |x - a| < \delta \implies \bigg |\frac{f'(x)}{g'(x)} - L \bigg | < \epsilon \]

  이 \(\delta\) 가 \(L = \displaystyle \lim_{x \to a} \frac{f(x)}{g(x)}\) 도 만족시킨다는 것을 보일 것이다. ▲

  일단 \(a < x\) 인 \(x \in V_{\delta}(a)\) 를 선택할 수 있다. 이제 닫힌 구간 \([a, x]\) 에서 함수 \(f, g\) 에 코시 평균값 정리를 적용하면 다음을 만족하는 점 \(c \in (a, x)\) 가 존재한다.

  \[ \frac{f'(c)}{g'(c)} = \frac{f(x) - f(a)}{g(x) - g(a)} = \frac{f(x)}{g(x)} \]

  이 \(c\) 는 \(0 < |c - a| < \delta\) 를 만족시키므로 다음이 성립한다.

  \[ 0 < |x - a| < \delta \implies \bigg |\frac{f(x)}{g(x)} - L \bigg | = \bigg |\frac{f'(c)}{g'(c)} - L \bigg | < \epsilon \]

  ■

• 증명

  임의의 양수 \(\epsilon\) 에 대하여 \(\displaystyle \lim_{x \to a} \frac{f'(x)}{g'(x)} = L\) 이므로 모든 \(a < x < a + \delta_1\) 에 대하여 다음을 만족시키는 \(\delta_1 > 0\) 이 존재한다.

  \[ \bigg |\frac{f'(x)}{g'(x)} - L \bigg | < \dfrac{\epsilon }{2} \tag{1} \]

  \(t\) 를 고정된 값 \(t = a + \delta_1\) 으로 두자. ▲

  모든 \(x \in (a, t)\) 에 대하여 구간 \([x, t]\) 에서 코시 평균값 정리를 적용하면 다음을 만족하는 \(c \in (x, t)\) 를 얻는다.

  \[ \frac{f(x) - f(t)}{g(x) - g(t)} = \frac{f'(c)}{g'(c)} \]

  \((1)\) 이 \(a < x < a + \delta_1\) 에 대하여 성립하므로 모든 \(x \in (a, t)\) 에 대하여 다음이 성립한다.

  \[ L - \dfrac{\epsilon }{2} < \frac{f(x) - f(t)}{g(x) - g(t)} < L + \dfrac{\epsilon }{2} \tag{2} \]

  \((2)\) 에 \(\dfrac{g(x) - g(t)}{g(x)}\) 를 곱하여 \(\dfrac{f(x)}{g(x)}\) 를 분리시키려 한다. 이를 위하여 먼저 이 값이 양수임을 보이려 하는데 이는 \(1 > \dfrac{g(t)}{g(x)}\) 를 보이는 것과 같다. \(\displaystyle \lim_{x \to a} g(x) = \infty\) 이므로 모든 \(a < x < a + \delta_2\) 에 대하여 \(g(x) > g(t)\) 을 만족하게 하는 \(\delta_2 > 0\) 가 존재한다. 이제 \((2)\) 에 이 값을 곱하면 다음을 얻는다.

  \[ \bigg ( L - \dfrac{\epsilon }{2} \bigg ) \bigg (1 - \frac{g(t)}{g(x)} \bigg ) < \frac{f(x) - f(t)}{g(x)} < \bigg ( L + \dfrac{\epsilon }{2} \bigg ) \bigg (1 - \frac{g(t)}{g(x)} \bigg ) \iff \]
  \[ L - \dfrac{\epsilon }{2} + \frac{-L g(t) + \epsilon /2 g(t) + f(t)}{g(x)} < \frac{f(x)}{g(x)} < L + \dfrac{\epsilon }{2} + \frac{-L g(t) - \epsilon /2 g(t) + f(t)}{g(x)} \tag{3} \]

  \(\displaystyle \lim_{x \to a} g(x) = \infty\) 이므로 \(a < x < a + \delta_3\) 일 때 \(g(x)\) 가 충분히 커서 다음 두 식의 절댓값이 모두 \(\epsilon /2\) 보다 작아지도록 하는 \(\delta_3\) 가 존재한다.

  \[\dfrac{-L g(t) + \epsilon /2 g(t) + f(t)}{g(x)}, \quad \dfrac{-L g(t) - \epsilon /2 g(t) + f(t)}{g(x)}\]

  \(\delta = \min \{\delta_1,\delta_2, \delta_3\}\) 를 택하면 모든 \(a < x < a + \delta\) 에 대하여 \((3)\) 은 다음과 같다.

  \[ \bigg | \frac{f(x)}{g(x)} - L\bigg | < \epsilon \]

  ■

Differentiation Rules✔

Differentiation is linear✔

• 라이프니츠 표기법으로 미분이 선형임을 표현하면 다음과 같다.

  \[ \frac{d(af + bg)}{dx} = a \frac{df}{dx} + b \frac{dg}{dx} \]

• 증명

  미분가능한 함수와 사칙연산에 의하여 쉽게 증명가능하다. ■

Product Rule✔

• 라이프니츠 표기법

  \[ \frac{d(fg)}{dx} = \frac{df}{dx}g + f\frac{dg}{dx} \]

• 증명

  미분가능한 함수와 사칙연산와 같은 논리로 증명 가능하다.

Chain Rule✔

• 라이프니츠 표기법

  \[ \frac{d}{dx}h(x) = \frac{d}{dz}f(z)| _{z = g(x)} \cdot \frac{d}{dx}g(x) \]

  또는 다음과 같이 축약되어 표기할 수도 있다.

  \[ \frac{dh(x)}{dx} = \frac{df(g(x))}{dg(x)} \cdot \frac{dg(x)}{dx} \]

  \(y = h(u), u = g(x)\) 로 두면 다음이 성립한다.

  \[ \frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx} \]
  \[ \frac{dy}{dx} = \frac{dh(u)}{du} \cdot \frac{dg(x)}{dx} \]

• 오일러 표기법

  미분 연산자 \(D\) 를 사용한 오일러 표기법으로 연쇄법칙을 다음과 같이 쓸 수 있다.

  \[ [D(f \circ g)]_{x} = [Df]_{g(x)} \cdot [Dg]_{x} \]

• 증명

  정리 5.2.5 연쇄법칙과 같은 논리로 증명된다. ■

• 예시

  \[ \frac{d \sin (2x ^{2}) }{dx} = \frac{d \sin (t)}{d t} \frac{d2x ^{2}}{dx} = \cos (t) \cdot 4x = 4x\cos (2x ^{2}) \]

Inverse Function Rule✔

• 라이프니츠 표기법

  \[ \frac{dx}{dy} = \frac{1}{\frac{dy}{dx}} \]

  이에 따라 \(\displaystyle \frac{dx}{dy}\cdot \frac{dy}{dx} = 1\) 이 성립한다.

• 예시

  \(y = x^2\) 는 역함수 \(x = \sqrt[]{y}\) 를 가진다. 따라서 \(\dfrac{dy}{dx} = 2x\) 이고 다음이 성립한다.

  \[ \frac{dx}{dy} = \dfrac{1}{\frac{dy}{dx}} = \frac{1}{2x} = \frac{1}{2 \sqrt[]{y}} \]

  이 결과는 역함수의 도함수의 공식 \(\displaystyle [f ^{-1}]' = \frac{1}{f' \circ f ^{-1}}\) 을 사용하여 도함수를 구한 것과 똑같다. 또한 다음이 성립한다.

  \[ \frac{dy}{dx} \cdot \frac{dx}{dy} = 2x \cdot \frac{1}{2x} = 1 \]

• 증명

  \(f(f ^{-1}(y)) = y\) 을 \(y\) 에 대하여 미분하면 연쇄법칙에 의하여 다음이 성립한다.

  \[ f'(f ^{-1}(y)) \cdot [f ^{-1}]'(y) = 1 \]
  \[ \iff [f ^{-1}]'(y) = \frac{1}{f'(f ^{-1}(y))} \]

  ■

Reciprocal rule✔

• 라이프니츠 표기법

  \[ \frac{d(1/f)}{dx} = - \frac{1}{f^2}\frac{df}{dx} \]

• 증명

  nonvanishing 함수 \(f(x)\) 가 미분가능하면 다음이 성립한다.

  \[ \begin{align}\begin{split} \lim_{h \to 0} \frac{\frac{1}{f(x+h)} - \frac{1}{f(x)}}{h} &= \lim_{h \to 0} \frac{-\frac{f(x+h)-f(x)}{f(x+h)f(x)}}{\frac{h}{1}} = -\lim_{h \to 0} \frac{f(x+h)-f(x)}{hf(x+h)f(x)} \\ &= - \lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \cdot \frac{1}{f(x+h)f(x)} \\ &= - \lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \circ \lim_{h \to 0} \frac{1}{f(x+h)f(x)} \\ &= - f'(x) \cdot \frac{1}{\{f (x)\} ^{2}}\\ \end{split}\end{align} \tag*{} \]

  ■

Quotient rule✔

• 증명

  미분가능한 두 함수 \(f(x),g(x)(g(x) \neq 0)\) 에 대하여 Product rule, Reciprocal rule 에 의하여 다음이 성립한다.

  \[ \begin{align}\begin{split} \left\{ \frac{f(x)}{g(x)} \right\}'&= \left\{f(x) \cdot \frac{1}{g(x)}\right\}' = f'(x) \cdot \frac{1}{g(x)} + f(x) \cdot \left\{\frac{1}{g(x)}\right\}' \\ &=\frac{f'(x)}{g(x)} - f(x) \cdot \frac{g'(x)}{\{g(x)\} ^{2}} = \frac{f'(x)g(x) - f(x)g'(x)}{\{g(x)\} ^{2}} \end{split}\end{align} \tag*{}\]

Derivative of exponential function✔

• 증명

  1:

  \[ \lim_{x \to 0} \frac{\log_{a} (1+x)}{x} = \lim_{x \to 0} \log_{a} (1+x) ^{1/x} = \log_{a} \left( \lim_{x \to 0} (1 + x) ^{1/x} \right) = \log_{a} e = \frac{1}{\ln a} \tag*{■} \]

  2:

  \(a ^{x} -1 = t\) 로 두면 \(x \to 0 \implies t \to 0\) 이고, \(x = \log_{a} (1+t)\) 이므로 다음이 성립한다.

  \[ \begin{align}\begin{split} \lim_{x \to 0} \frac{a ^{x}-1}{x} &= \lim_{t \to 0} \frac{t}{\log_{a} (1+t)} = \lim_{t \to 0} \frac{1}{\frac{\log_{a} (1+t)}{t}} \\ &= \lim_{t \to 0} \frac{1}{\log_{a} (1+t) ^{1/t}} = \frac{1}{\log_{a} e} = \ln a \\ \end{split}\end{align} \tag*{} \]

  ■

• 증명

  1:

  지수함수 \(f(x) = a ^{x}(a>0, a \neq 1)\) 의 미분은 다음과 같다.

  \[ \begin{align}\begin{split} \lim_{h \to 0} \frac{f(a+h)-f(a)}{h} &= \lim_{h \to 0} \frac{a ^{x+h}-a ^{x}}{h} = \lim_{h \to 0} \frac{a ^{x}(a ^{h}-1)}{h} \\ &= a ^{x} \lim_{h \to 0} \frac{a ^{h}-1}{h} = a ^{x} \ln a \\ \end{split}\end{align} \tag*{}\]

  ■

  2:

  1) 의 결과에 \(a = e\) 를 대입하면 바로 나온다. ■

Derivative of logarithmic function✔

• 증명

  1:

  로그함수 \(y=\log_{a} x(a>0, a \neq 1)\) 에 대하여 다음이 성립한다.

  \[ \begin{align}\begin{split} \lim_{h \to 0} \frac{f(x+h)-f(x)}{h} &= \lim_{h \to 0} \frac{\log_{a} (x+h)-\log_{a} x}{h} = \lim_{h \to 0} \frac{1}{h} \log_{a} \frac{x+h}{x} \\ &= \lim_{h \to 0} \frac{1}{x} \cdot \frac{x}{h} \log_{a} \left(1+\frac{h}{x}\right) = \frac{1}{x} \lim_{h \to 0} \log_{a} \left(1+\frac{h}{x}\right) ^{x/h} \\ \end{split}\end{align} \tag*{}\]

  이때 \(\dfrac{h}{x} = t\) 로 두면 \(h \to 0 \implies t \to 0\) 이므로 다음이 성립한다.

  \[ = \frac{1}{x} \lim_{t \to 0} \log_{a} (1 + t)^{1/t} = \frac{1}{x}\log_{a} e = \frac{1}{x\ln a} \]

  ■

  2:

  \(a = e\) 를 대입하면 바로 나온다. ■

Power rule✔

• 증명(https://en.wikipedia.org/wiki/Power_rule)

  \(x > 0\) 인 경우 실수 제곱의 정의 에 의하여 \(f(x) = x ^{r} = e ^{r \ln x}\) 이고, 다음이 성립한다.

  \[ f'(x) = \frac{r}{x} e ^{r \ln x} = \frac{r}{x}x ^{r} = rx ^{r-1} \]

  ▲

  \(x < 0\) 인 경우 \(x ^{r} = ((-1)(-x)) ^{r} = (-1)^{r}(-x)^{r}\) 이므로 \(-x > 0\) 이 되어 실수 제곱의 정의를 사용하여 똑같은 방식으로 \(f'(x) = rx ^{r-1}\) 임을 증명할 수 있다.

  그러나 \((-1)^{r}\) 은 \(r\) 이 무리수일 때 정의되지 않고, 짝수 분모를 갖는 유리수일 때는 허수가 된다. 즉, 이 경우에는 \(r\) 이 반드시 홀수 분모를 갖는 유리수여야만 성립한다. ▲

  \(x = 0\) 일 때의 미분은 다음과 같다.

  \[ \lim_{h \to 0} \dfrac{h ^{r} - 0 ^{r}}{h} \]

  이 값은 \(r\) 이 \(r > 1\) 이고 홀수 분모를 갖는 유리수일 때 \(0\) 이고, \(r = 1\) 일 때 \(1\) 이다. 그 이외의 경우 \(h ^{r}\) 은 \(h < 0\) 일 때 정의되지 않거나 실수가 아니게 된다. ▲

  \(x = 0, r = 0\) 인 경우 즉, \(0 ^{0}\) 인 경우도 제외된다. 왜냐하면 함수 \(f(x, y) = x ^{y}\) 가 \((0, 0)\) 에서 극한을 갖지 않기 때문이다. 극한이 존재하지 않는 이유는 \(x ^{0}\) 은 \(x\) 가 \(0\) 으로 다가갈 때 \(1\) 로 다가가는데 비해, \(0 ^{y}\) 은 \(y\) 가 \(0\) 으로 다가갈 때 \(0\) 으로 다가가기 때문이다. 이 경우를 어떤 경우에 포함시키든 모순이 발생한다. 따라서 관례적으로 이 경우는 정의하지 않은채로 내버려둔다. ■

Generalized Power rule✔

• power rule 은 일반화될 수 있는데 이 정리가 가장 일반화된 power rule 이다. 이 정리가 특수화된 대표적인 경우는 다음과 같다.

  • \(f(x) = x ^{a}\) 일 경우 \(a \in \R _{\neq 0}, x \in \R _{> 0}\) 일 때 \(f'(x) = ax ^{a-1}\) 이다.

  • \(g(x) = -1\) 이 되면 reciprocal rule 이 된다.

• 증명

  \[ \begin{align}\begin{split} (e ^{g \ln f})'&= (g \ln f)' \cdot e ^{g \ln f} \\ &= (g' \ln f + g \cdot (\ln f)') \cdot e ^{g \ln f} \\ &= \left( g' \ln f + g \cdot \left( f' \cdot \frac{1}{f}\right)\right) \cdot f ^{g } \\ \end{split}\end{align} \tag*{} \]

  ■

Derivatives of trigonometric functions✔

• 증명

  1:

  사인함수의 테일러 급수는 \(\R\) 에서 사인함수로 수렴한다. 그런데 멱급수는 수렴구간 \(\R\) 에서 미분가능하다. 그러면 코사인 함수의 멱급수 전개에 의하여 다음이 성립한다.

  \[ (\sin x)' = \sum_{n=0}^{\infty}(-1)^{n}\dfrac{x ^{2n+1}}{(2n + 1)!} = \sum_{n=0}^{\infty}(-1)^{n}\dfrac{x ^{2n}}{(2n)!} = \cos x \tag*{■} \]

  2:

  코사인함수의 테일러 급수는 \(\R\) 에서 코사인함수로 수렴한다. 그런데 멱급수는 수렴구간 \(\R\) 에서 미분가능하다. 그러면 사인 함수의 멱급수 전개에 의하여 이 증명이 성립한다. ■

  3:

  지금까지 증명해온 미분법을 기반으로 이 증명에 의하여 쉽게 증명된다.

  4:

  지금까지 증명해온 미분법을 기반으로 이 증명에 의하여 쉽게 증명된다.

  5:

  지금까지 증명해온 미분법을 기반으로 이 증명에 의하여 쉽게 증명된다.

  6:

  지금까지 증명해온 미분법을 기반으로 이 증명에 의하여 쉽게 증명된다.

• 역삼각함수의 도함수들의 정의역은 역삼각함수의 정의역에 따른다.

• 증명

  지금까지 정리된 미분법들을 기반으로 다음의 증명들에 의하여 쉽게 증명할 수 있다.

  1: https://proofwiki.org/wiki/Derivative_of_Arcsine_Function

  2: https://proofwiki.org/wiki/Derivative_of_Arccosine_Function

  3: https://proofwiki.org/wiki/Derivative_of_Arctangent_Function

  4: https://proofwiki.org/wiki/Derivative_of_Arccotangent_Function

  5: https://proofwiki.org/wiki/Derivative_of_Arcsecant_Function

  6: https://proofwiki.org/wiki/Derivative_of_Arccosecant_Function

Derivatives of hyperbolic functions✔

• 증명

  1:

  \[ \frac{d}{dx} \sinh x= \frac{d}{dx}\left( \dfrac{e ^{x} - e ^{-x}}{2} \right) = \dfrac{e ^{x} + e ^{-x}}{2} = \cosh x \tag*{■} \]