Continuity
Contents
Continuity✔
정의 4.3.1 연속성(Continuity)
함수
-
직관적으로 펜을 떼지 않고 그래프를 그릴 수 있으면 연속함수라 한다.
-
이 정의는 고등학교 때 배웠던 연속의 정의를 엄밀하게 바꾼 것이다. 즉, 다음이 성립하면 함수
-
-
-
-
-
함수의 극한과 정의가 비슷하다. 극한의 정의에서 첫번째 부등식은
였다. 이는
함수의 극한에서는 점
-
예시(https://math.stackexchange.com/questions/1924770/why-is-y-1-x-a-continuous-function-but-not-y-1-x2)
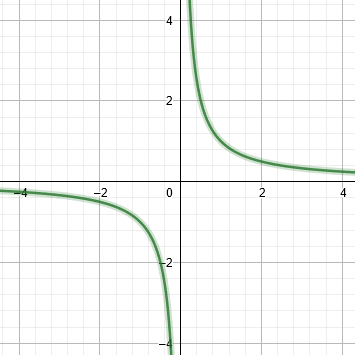
같은 이유로
는 불연속함수이지만
은 연속함수이다.
-
만약
정리 4.3.2
함수
-
임의의
-
-
-
증명
1:
단지 절댓값 표현을 위상수학의 근방으로 표현한 것이다. ■
2:
3:
역으로
문제 4.3-5
-
증명
Criterion for Discontinuity✔
따름정리 4.3.3 불연속성 판정법(Criterion for Discontinuity)
함수
-
정리 4.3.2(2) 는 함수가 어떤 점에서 연속이 아님을 보이는데 유용하다.
-
증명
단지 정리 4.3.2(2) 을 부정한 것 뿐이다. ■
Algebraic Continuity Theorem✔
정리 4.3.4 연속성과 사칙연산(Algebraic Continuity Theorem)
두 함수
-
임의의
-
-
-
-
증명
따름정리 4.2.4 와 정리 4.3.2 로 쉽게 증명할 수 있다. ■
-
예시
상수함수
그러면 정리에 의하여 임의의 다항함수
Composition of Continuous Functions✔
정리 4.3.9 연속함수의 합성(Composition of Continuous Functions)
두 함수
-
증명
즉, 임의의 양수
그러므로
Continuous Functions on Compact Sets✔
정리 4.4.1 콤팩트 집합의 보존(Preservation of Compact Set)
연속함수
-
증명
임의의 수열
Extreme Value Theorem✔
정리 4.4.2 최대-최소 정리(extreme value theorem)
함수
-
이 정리는 콤팩트 집합
-
증명
정리 4.4.1 에 의하여 연속함수는 콤팩트 집합을 보존하므로
Uniformly Continuous✔
정의 4.4.4 균등 연속(고른 연속, uniformly continuous)
임의의
을 만족하게 하는
-
을 만족하게 하는
-
함수
을 만족하게 하는
-
따라서
따라서
위 예시에서
실제로 다음과 같은
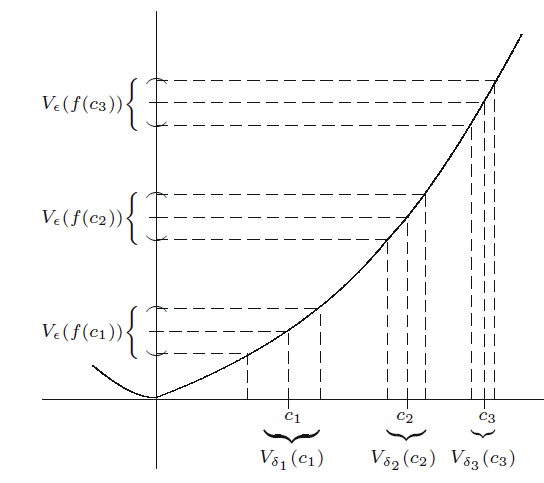
균등 연속이란

정리 4.4.5 균등 연속 판정법
함수
-
참고 : 논의영역
-
증명
먼저
정의 4.4.4 균등 연속의 부정은 다음과 같다.
즉,
그러면 임의의
역으로
Uniform Continuity Theorem✔
정리 4.4.7 콤팩트 집합에서의 균등 연속
콤팩트 집합
-
그러나 유계인 정의역에서 연속인 함수가 반드시 균등 연속이라는 보장은 없다. 가령 다음과 같은
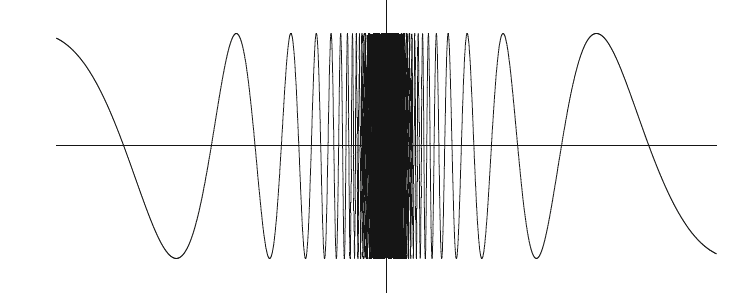
하지만 이 정리는 콤팩트한 정의역에서 연속인 함수는 반드시 균등 연속임을 보장해준다.
-
증명
즉, 수열
즉,
그러나 임의의
Intermediate Value Theorem✔
정리 4.5.1 사잇값 정리(intermediate value theorem)
연속함수
-
이 정리는 닫힌 구간
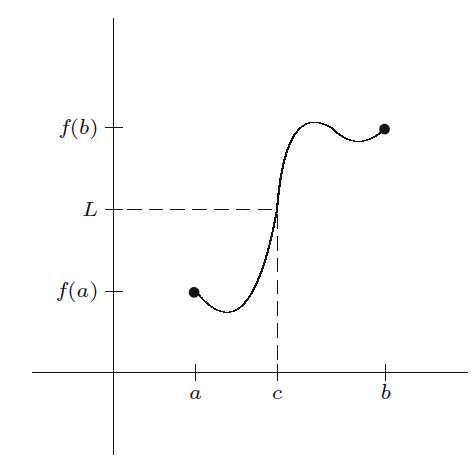
-
정리 4.5.2 을 사용한 증명
-
사잇값 정리는 보통 근의 존재성을 증명하는데 사용된다. 가령
그런데
-
완비성 공리를 사용한 증명
잠시
위와 같이 정의된
수론 정리 2.3.1, 수론 정리 2.4.2에 의하여 다음 중 오직 한 경우만 성립한다.
즉,
-
축소구간성질을 사용한 증명
잠시
이 방법으로 닫힌구간열
이는
정리 4.5.2
연속함수
-
이 정리는 연속함수가 연결집합을 보존한다는 것을 말해준다.
-
증명
다음과 같이
함수의 정의 에 의하여
Intermediate Value Property✔
정의 4.5.3 사잇값 성질(Intermediate Value Property)
구간
-
이 정의를 사용하면 정리 4.5.1 사잇값 정리를 다음과 같이 말할 수 있다.
연속함수는 사잇값 성질을 가진다. -
그렇다면 사잇값 정리의 역은 성립할까? 즉, 함수가 사잇값 성질을 가지면 연속함수 인가? 그렇지 않다.
-
증명
함수
그러나 단조함수가 사잇값 성질을 가지면 연속함수이다.
-
Sets of Discontinuity✔
불연속점 집합(Sets of Discontinuity)
함수
Monotone Function✔
정의 4.6.1 단조함수(monotone function)
함수
-
-
-
증가함수 또는 감소함수를 단조함수라 한다.
Classification of Discontinuity✔
불연속성의 분류
불연속성은 다음 3가지로 분류된다.
-
극한
-
-
그 외의 이유로 극한
-
다음은 제거 가능함 불연속의 예시이다.

-
다음은 비약 불연속점의 예시이다.

-
다음은 본질적 불연속점의 예시이다.

위 그래프는 다음 함수로 그린 것이며
문제 4.6-5
단조함수가 가지는 불연속점은 비약 불연속점이다.
-
임의의 함수의 불연속점을 밝히는 것은 약간 까다롭지만, 이렇게 단조함수일 때는 불연속점들이 비약 불연속점 뿐이다.
-
증명
정의 4.6.5
- 이 정의는 연속의 정의에서 "임의의
문제 4.6.8
주어진
-
증명
먼저
이 성립함을 의미한다. ▲
이제
그런데
따라서
Topological Structure of Discontinuous Set✔
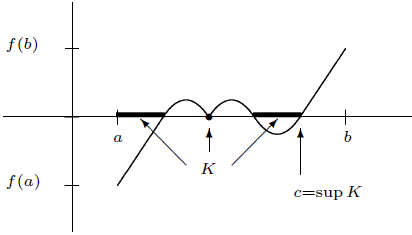
정리 4.6.6
임의의 함수
-
지금까지의 논의의 결론이 이 정리이다. 이 정리는
-
증명
먼저
그러면
이제 주어진
따라서
즉,
이제
따라서
이제
한편 주어진
이로써