Functional Limit

Functional Limit✔

• 함수의 극한(proofwiki)의 정의와 같다. 보편 양화사 $\forall$ 나 존재 양화사 $\exists$ 를 술어 $P$ 에 지칭하면 다음과 같은 형태가 된다.

  $$\forall x : P$$

  이때 이 명제 자체를 $Q = \forall x : P$ 로 두고 $Q$ 에 또 다시 양화사를 지칭하면 다음과 같이 된다.

  $$\exists y : Q$$

  이것을 풀어서 쓰면 이렇게 된다.

  $$\exists y : \forall x : P$$

• 정의역의 원소 $x \in A$ 가 $c$ 에 가까워지는데, $c$ 가 $A$ 의 극한점이므로 $A$ 가 닫힌 집합이 아닌 경우 $c \not\in A$ 인데, 이 경우에도 함수의 극한이 잘 정의된다. 이는 $c$ 가 $f$ 의 정의역에 속하지 않아도 극한을 정의할 수 있음을 뜻한다.

• $0 < |x - c|$ 라는 조건은 $x \neq c$ 라는 것을 간결하게 말하기 위하여 추가된 것 뿐이다.

• $x \in A$ 라는 조건은 $x$ 에서 함수 $f$ 가 정의되어 있다는 것을 보장해준다. 하지만 보통 $f(x)$ 라는 표현 자체에 $x$ 에서 함수 $f$ 가 정의되어 있다는 것을 함축하여 $x \in A$ 라는 조건을 생략한다.

• 정의역의 고립점에서의 함수의 극한은 정의하지 않는다. 왜냐하면 고립점에서의 근방은 정의역과 교집합을 갖지 않기 때문에, 정의역의 원소 $x$ 가 고립점으로 가까이 다가가는 것을 생각할 수 없기 때문이다. 따라서 정의역의 극한점에서만 함수의 극한을 생각한다.

• 이렇게 극한을 엄밀하게 정의하는 것을 엡실론-델타 논법($\epsilon-\delta$ 논법)이라 한다.

• 함수의 극한을 위상적으로 표현할 수 있는 것은 다음이 성립하기 때문이다.

  $$|f(x) - L| < \epsilon \iff f(x) \in V_{\epsilon}(L)$$
  $$|x-c| < \delta \iff x \in V_{\delta}(c)$$

  함수의 극한을 위상적으로 생각하면 함수의 극한을 다음과 같이 기하학적으로 쉽게 이해할 수 있다.

  

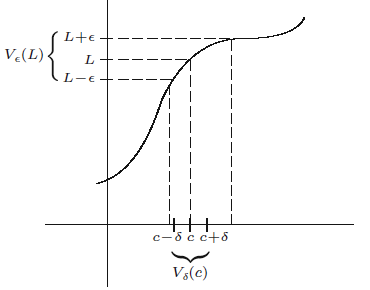
• 예시

  $f(x) = 3x + 1$ 에 대하여 $\displaystyle \lim_{x \to 2} f(x) = 7$ 를 증명해보자. 임의의 양수 $\epsilon$ 에 대하여 다음을 만족시키는 양수 $\delta$ 의 존재성을 보이면 된다.

  $$0 < |x - 2| < \delta \implies |f(x) - 7| < \epsilon$$

  $|f(x) - 7| = |3x - 6| = 3|x - 2|$ 이므로 $\delta = \epsilon /3$ 으로 택하면 다음이 성립한다.

  $$0 < |x-2| < \delta \implies |f(x) - 7| = 3|x - 2| < 3(\epsilon /3) = \epsilon$$

  따라서 $\displaystyle \lim_{x \to 2} f(x) = 7$ 이다.

• 예시

  $g(x) = x ^{2}$ 에 대하여 $\displaystyle \lim_{x \to 2} g(x) = 4$ 를 증명해보자. 임의의 양수 $\epsilon$ 에 대하여 다음을 성립시키는 $\delta$ 가 항상 존재한다는 것을 보이면 된다.

  $$0 < |x-2| < \delta \implies |g(x) - 4| < \epsilon$$

  $|g(x) - 4| = |x + 2||x - 2|$ 인데 $x$ 가 $2$ 로 다가가는 극한이므로 $|x - 2|$ 는 임의로 작게 만들 수 있다. 따라서 $|x - 2|$ 는 걱정할 필요가 없다.

  $c = 2$ 를 중심으로 하는 $\delta$-근방의 반지름이 $\delta = 1$ 보다 크지 않는 한 다음이 성립한다.

  $$\forall x \in V_{\delta}(c) \setminus \{c\} : |x + 2| \leq |3 + 2| = 5$$

  따라서 $\sup |x + 2| = 5$ 이다. 그러면 $\delta = \min \{1, \epsilon /5\}$ 에 대하여 다음이 성립한다.

  $$0 < |x - 2| < \delta \implies |x ^{2} - 4| = |x + 2||x - 2| < 5 \cdot \dfrac{\epsilon }{5} = \epsilon$$

  따라서 $\displaystyle \lim_{x \to 2} g(x) = 4$ 이다.

Sequential Criterion for Functional Limits✔

• 증명

  $1 \implies 2$:

  1) 을 가정했으므로 임의의 양수 $\epsilon$ 와 $c \neq x$ 인 $x \in A$ 에 대하여 $x \in V_{\delta}(c)$ 이면 $f(x) \in V_{\epsilon}(L)$ 인 $V_{\delta}(c)$ 가 항상 존재한다. 2) 의 가정부에 의하여 $x_n \neq c$ 인 임의의 수열 $(x_n) \subset A$ 이 $(x_n) \to c$ 이므로 어떤 항 $x_N$ 이후에 항상 $x_n \in V_{\delta}(c)$ 이다. 그러면 1) 에 의하여 $n \geq N$ 일 때 $f(x) \in V_{\epsilon}(L)$ 이다. ■

  $2 \implies 1$:

  2) 를 가정하고 $\displaystyle \lim_{x \to c} f(x) \neq L$ 라고 두자. 이는 어떤 양수 $\epsilon_0$ 에 대응하는 적절한 $\delta$ 가 존재하지 않는다는 것이다. 즉, $\delta >0$ 를 어떻게 정하든지 다음을 만족하는 $x$ 가 적어도 하나 존재한다.

  $$x \neq c \land x \in V_{\delta}(c) \implies f(x) \not\in V_{\epsilon_0}(L)$$

  그렇다면 $\delta _n = 1/n$ 으로 두어도, 각 $n \in \N$ 마다 다음을 만족하는 $x_n \in V_{\delta_n}(c)$ 를 선택할 수 있다.

  $$x_n \neq c \land x_n \in V_{\delta_n}(c) \implies f(x_n) \not\in V_{\epsilon_0}(L)$$

  이는 $x_n \neq c \land (x_n) \to c$ 인 어떤 수열 $(x_n)$ 에 대한 함숫값 수열 $f(x_n)$ 이 $L$ 로 수렴하지 않음을 의미한다. 이는 2) 와 모순이다. 따라서 $\displaystyle \lim_{x \to c} f(x) = L$ 이다. ■

Algebraic Limit Theorem for Functional Limits✔

• 증명

  수열의 극한의 사칙연산과 정리 4.2.3 에 의하여 쉽게 증명된다. ■

Divergence Criterion for Functional Limits✔

• 이 정리는 어떤 지점으로 다가가는 모든 수열의 극한값이 똑같지 않으면 발산한다는 것을 말해준다. 그래서 정리 4.2.3 은 어떤 지점으로 다가가는 모든 수열의 극한값이 똑같아야 극한이 정의된다는 것을 말해준다.

• 예시

  다음과 같은 함수 $y = \sin \dfrac{1}{x}$ 가 $0$ 에서 극한을 가지지 않음을 증명하자.

  

  $x_n = 1/2n \pi , y_n = 1/(2n \pi + \pi /2)$ 이면 $\lim x_n = \lim y_n = 0$ 이지만 $\lim \sin (1/x_n) = 0 \neq \lim \sin (1/y_n) = 1$ 이다. 따라서 $\displaystyle \lim_{x \to 0} \sin (1/x)$ 은 존재하지 않는다.

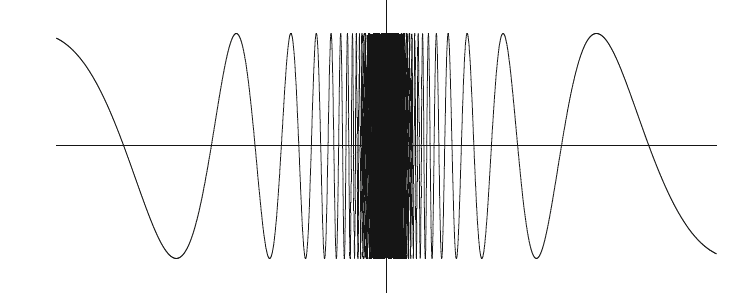
Divergence to Infinity✔

• 예시

  $\displaystyle \lim_{x \to 0} \dfrac{1}{x ^{2}} = \infty$ 를 증명해보자. $\delta = \displaystyle \sqrt[]{\frac{1}{M}}$ 로 두면 다음이 성립한다.

  $$0 < |x| < \delta \implies x ^{2} < \frac{1}{M} \implies M < \frac{1}{x^2}$$

  따라서 $\displaystyle \lim_{x \to 0} \dfrac{1}{x ^{2}} = \infty$ 이다.

• 예시

  $\displaystyle \lim_{x \to \infty} \frac{1}{x} = 0$ 을 증명해보자. $K = \dfrac{1}{\epsilon }$ 으로 두면 다음이 성립한다.

  $$x > K = \frac{1}{\epsilon } \implies \frac{1}{x} < \epsilon$$

  따라서 $\displaystyle \lim_{x \to \infty} \frac{1}{x} = 0$ 이다.

• 예시

  $\displaystyle \lim_{x \to \infty} \sqrt[]{x} = \infty$ 임을 증명해보자. $K = M^2$ 로 두면 다음이 성립한다.

  $$K < x \implies M < \sqrt[]{x}$$

  따라서 $\displaystyle \lim_{x \to \infty} \sqrt[]{x} = \infty$ 이다.

Left and Right-Hand Limit✔

• 증명

  $\implies$:

  $\displaystyle \lim_{x \to c} f(x) = L$ 를 가정하면 임의의 양수 $\epsilon$ 에 대하여 다음을 만족하게 하는 $\delta$ 가 존재한다.

  $$0 < | x - c | < \delta \implies |f(x) - L| < \epsilon$$

  이는 좌극한과 우극한의 정의를 만족시킨다. ■

  $\impliedby$:

  좌극한과 우극한을 가정하면 임의의 양수 $\epsilon$ 에 대하여 다음을 만족하게 하는 양수 $\delta_1, \delta _2$ 가 존재한다.

  $$0 < x - c < \delta_1 \implies |f(x) - L| < \epsilon$$
  $$0 < c - x < \delta_2 \implies |f(x) - L| < \epsilon$$

  $\delta = \min \{\delta _1, \delta _2\}$ 를 정의하면 다음이 성립한다.

  $$0 < | x - c | < \delta \implies |f(x) - L| < \epsilon$$

  이로써 증명이 끝났다. ■