Function Sequence and Series
Contents
Function Sequence✔
Pointwise Convergence✔
정의 6.2.1 함수열의 점별수렴(pointwise convergence of function sequence)
각
-
-
예시
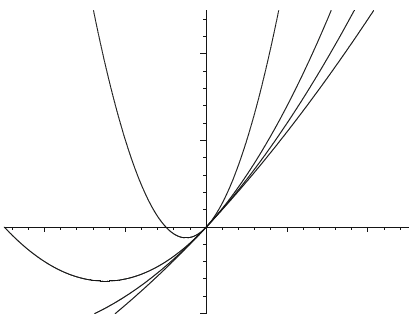
-
함수열을 이루는 함수가 연속이어도 극한 함수가 불연속 일 수도 있다. 또한 함수열을 이루는 함수가 미분가능이어도 극한 함수가 미분불가능 일 수도 있다.
-
예시
구간
Uniform Convergence of Function Sequence✔
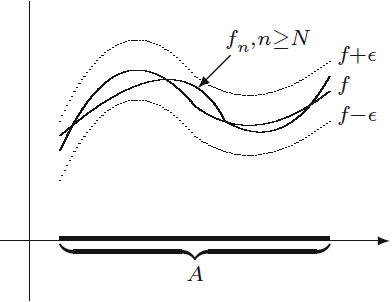
정의 6.2.3 함수열의 균등 수렴(고른 수렴, uniform convergence of function sequence)
-
이는 어떤
-
점별수렴과 균등 수렴을 차이를 이해하기 위하여 점별수렴을
"
점별 수렴의 경우
-
예시
함수
균등수렴 여부를 조사해보자.
그러면 주어진
정의에 의하여
-
예시
-
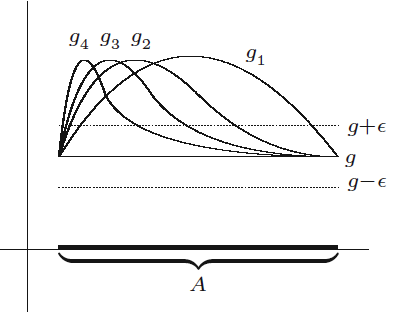
함수열
함수열
Cauchy Criterion for Uniform Convergence of Function Sequence✔
정리 6.2.5 함수열의 균등 수렴의 코시 판정법(cauchy criterion for uniform convergence)
집합
- 증명
Continuity of Limit Function✔
정리 6.2.6 함수열의 극한 함수의 연속
-
이 정리는 함수열의 극한 함수가 연속일 조건을 말해준다.
점별수렴하는 함수열의 함수들이 연속이어도 극한 함수가 불연속일 수도 있었다. 그러나 이 정리는 균등수렴하는 함수열의 함수들이 연속이면 극한 함수도 연속임을 말해준다.
-
증명
따라서 삼각부등식에 의하여 다음이 성립한다.
따라서
Differentiable of Limit Function✔
정리 6.3.1
닫힌 구간
-
이 정리는 점별수렴하는 미분가능한 함수열의 도함수열이 어떤 함수로 균등 수렴하면, 도함수열의 극한함수가 극한 함수의 도함수가 된다는 것을 말해준다.
-
하지만 사실은 도함수열
-
증명
임의의 양수를
▲
삼각부등식에 의하여 다음이 성립한다.
도함수열
▲
▲
▲
■
정리 6.3.2
닫힌 구간
-
증명
▲
임의의 양수를
그러면
한편, 함수열
▲
그러면
이
정리 6.3.3 함수열의 극한 함수의 미분가능성
닫힌 구간
-
정리 6.3.1 로부터 이어진 논증의 결론이 이 정리이고, 이 정리는 함수열의 극한 함수의 미분가능성의 조건을 말해준다.
-
이 정리는 정리 6.3.1 에 정리 6.3.2 를 적용하여 정리 6.3.1 보다 더 강한 정리를 얻어낸 것이다.
정리 6.3.1 는 점별수렴하는 미분가능한 함수열의 도함수열이 어떤 함수로 균등 수렴하면, 도함수열의 극한함수가 극한 함수의 도함수가 된다는 것을 말해준다. 정리 6.3.2 는 도함수열
따라서 정리 6.3.1 에서의 함수열
-
증명
정리 6.3.1 과 정리 6.3.2 를 종합한 결과이다. ■
Function Series✔
정의 6.4.1 함수급수(function series)
각
-
-
수열
두 경우 모두에서
-
Continuity of Function Series✔
정리 6.4.2 연속과 함수급수
집합
-
정리 6.2.6는 함수열의 극한함수가 연속일 조건을 말해주고, 이 정리는 함수급수의 극한함수가 연속일 조건을 말해준다.
-
증명
Differentiable of Function Series✔
정리 6.4.3 미분가능성과 함수급수
집합
-
함수급수
-
-
증명
부분합
Cauchy Criterion for Uniform Convergence of Function Series✔
정리 6.4.4 함수급수의 균등 수렴의 코시 판정법(cauchy criterion for uniform convergence)
함수급수
-
증명
부분합
Weierstrass M-test✔
따름정리 6.4.5 바이어슈트라스
각
무한급수
-
이 정리가 일반적으료 사용되는 균등수렴 판정법이다.
-
증명
그런데 다음이 성립하므로 정리 6.4.4 에 의하여
■
Power Series✔
멱급수(power series)
체
-
다음과 같은 중심이
정리 6.5.1
멱급수
-
절대수렴 판정법에 의하여 무한급수가 절대수렴하면 수렴한다. 이 정리는 멱급수가 어떤 점
수렴하는 점 집합이 유계 구간일 경우 부등식
이
-
증명
다음은 공비가
비교판정법에 의하여
Continuity of Power Series✔
정리 6.5.2
멱급수
-
증명
바이어슈트라스
보조정리 6.5.3 아벨의 보조정리(Abel's lemma)
-
증명
■
정리 6.5.4 아벨 정리(Abel's theorem)
반대로 멱급수가
-
아벨의 극한 정리(Abel's Limit Theorem)이라고도 부르지만 이 정리가 너무 유명해져서 극한을 빼고 아벨 정리라고 부른다.
-
이 정리는 유한 수렴반경을 갖는 멱급수가 수렴 반경 끝점에서 수렴하면, 그곳에서의 멱급수의 연속성을 보장해준다.
-
증명
먼저
■
정리 6.5.5
멱급수가 집합
-
이 정리와 정리 6.4.2 에 의하여 멱급수는 수렴하는 모든 지점에서 연속임을 알 수 있다.
정리 6.5.2, 보조정리 6.5.3, 아벨정리의 결론이 이 정리이다.
-
증명
문제 3.3-1에 의하여 콤팩트 집합
멱급수가 집합
Differentiable of Power Series✔
정리 6.5.6
임의의
-
정리 6.4.3
-
증명
먼저
비율 판정법에 의하여
이제
이에 따라 다음이 성립한다.
Properties of Power Series✔
정리 6.5.7
멱급수
-
-
-
-
-
지금까지의 논의의 결론이 이 정리이다.
-
이 정리는 멱급수를 직관적으로 이해하는 것을 허락해준다. 즉, 멱급수를 마치 다항함수처럼 받아들이는 것을 허락해준다. 수렴하는 구간에서 멱급수는 연속이고, 무한번 미분 가능하며, 도함수는 각 항을 미분하여 얻을 수 있다.
-
증명
1:
2, 3:
4:
미분한 급수도 멱급수이다. 정리 6.5.6 은 급수가 특정한 끝점에서 수렴하지 않을 수도 있지만 수렴반지름 자체는 불변함을 말해준다. 수학적 귀납법에 의하여 멱급수는 무한번 미분할 수 있다. ■
Taylor Series✔
정리 6.6.2 테일러 공식(Taylor's formula)
에 대하여 다음이 성립한다.
-
이 정리는 중심
즉, 위와 같은 중심
-
수학자들은
그렇다면 자연스럽게 "무한번 미분 가능한 성질 같이 미적분학에서 다루기 좋은 성질을 갖는 모든 함수를 멱급수로 나타내는 것이 가능한가?" 라는 질문이 생긴다. 또한 "만약
이 정리는 무한번 미분가능하고 멱급수 전개를 가지는 함수의 멱급수 계수를 알려준다.
-
증명
함수
따라서
테일러 급수(Taylor series)
무한히 미분 가능한 함수
-
-
예시
이로써 다음을 얻는다.
이 급수가
-
이렇게 멱급수 전개를 가지는 함수들을 쉽게 멱급수로 나타낼 수 있고, 정리 6.5.7 에 의하여 다항함수처럼 다룰 수 있어서 편하다. 그렇다면 그 역은 성립할까? 즉,
가
Lagrange's remainder theorem✔
정리 6.6.3 라그랑주 나머지항 정리(Lagrange's remainder theorem)
함수
-
이 정리는 테일러 급수가 원래의 함수와의 차이를 나타내는 오차함수를 쉽게 계산할 수 있도록 도와주고, 이로써 테일러 급수가 원래의 함수와 얼마나 다른 함수로 수렴하는지 판정할 수 있도록 해준다.
-
이 정리가 테일러 급수가 원래 함수로 수렴한다는 보장을 해주는 것이 아니다. 무한번 미분가능한 함수의 테일러 급수가 원래의 함수로 수렴하지 않는 경우도 있다.
-
예시
가령
팩토리얼은 지수함수보다 훨씬 빠르게 증가하므로 함수열
-
증명
양수
구간
이 과정을
■
Power Series Expansion for Sine/Cosine✔
사인함수 멱급수 전개
-
증명
이로써 다음을 얻는다.
이 급수가
가령
팩토리얼은 지수함수보다 훨씬 빠르게 증가하므로 함수열
코사인함수 멱급수 전개
- 증명
-
증명
사인함수의 멱급수 전개에 의하여 다음이 성립한다.
이 멱급수는
이 멱급수의 해는
이 식에
Analytic Function✔
실해석함수(real analytic function)
열린 구간
함수
- 위에서 살펴보았듯이 사인함수와 코사인함수는 해석함수이다.
The Weierstrass Approximation Theorem✔
정리 6.7.1 바이어슈트라스 근사 정리(Weierstrass approximation theorem)
연속함수
-
이 정리는 닫힌 구간에서 정의된 연속함수를 어떤 다항함수로 균등하게 근사시킬 수 있다는 것을 말해준다.
-
바이어슈트라스 근사 정리는 페예르 정리의 따름정리이다.
-
증명
Interpolation✔
정의 6.7.2 다각형 함수(polygonal)
연속함수
이 존재하면
-
Interpolation(보간)이란 주어진 점들을 지나가는 함수를 찾는 과정이다.
-
예시
가령 다음과 같은 점들을 지나는 다각형 함수가 있는 것은 자명하다.
한편, 함수
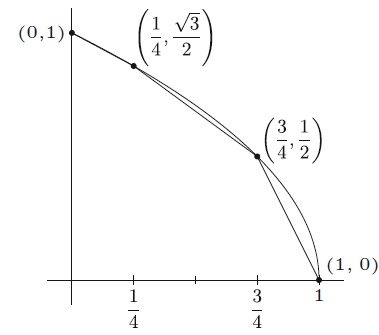
정리 6.7.3 은 이러한 다각형 함수가 연속함수에 항상 존재한다는 것을 보장해준다.
정리 6.7.3
연속함수
-
이 정리는 연속함수를 다각형 함수로 균등하게 근사시킬 수 있다는 것을 말해준다.
-
증명